背包模板
前言
Upd on 2025.3.23:原来图片链接炸了,换了新链接。
Upd on 2025.5.6:发现了一处笔误。
Upd on 2025.6.8:添加了有依赖背包(树形背包)的 \(O(nV)\) 做法。
01 背包
题目描述
有 \(n\) 个物品,一个体积为 \(V\) 的背包。
第 \(i\) 个物品体积为 \(v_i\),价值为 \(w_i\)。
每个物品只能选择一次,最大化放入背包物品的总价值。
输出最大总价值。
状态表示
集合
令 \(f_{i,j}\) 表示 从前 \(i\) 个物品中选,总体积不超过 \(j\) 的方案集合。
属性
集合中的 最大价值。
状态转移
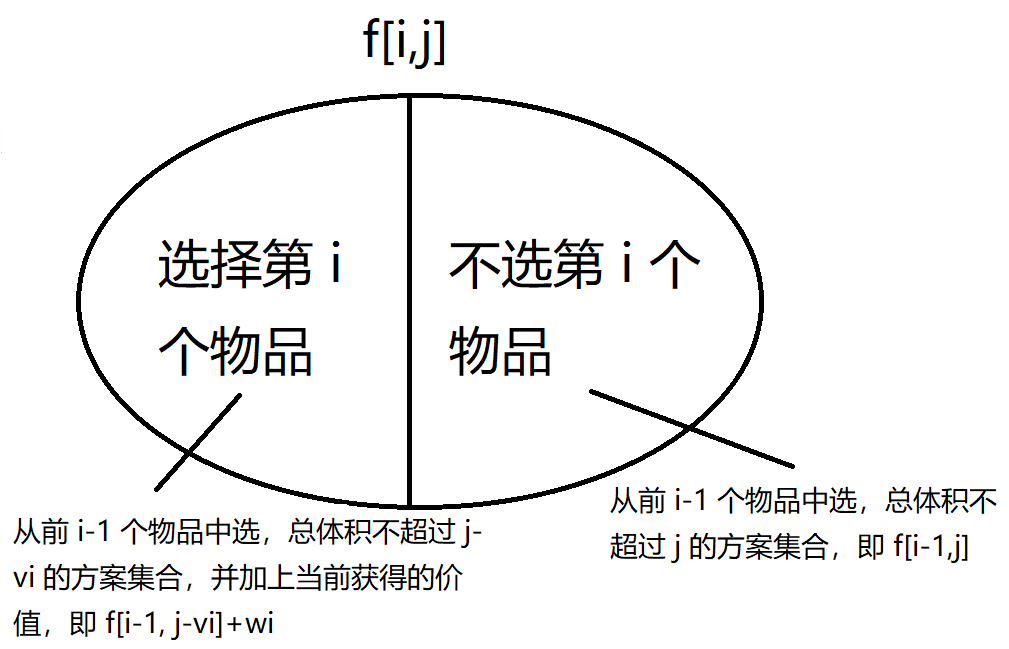
故
DP 时间复杂度为 \(O(nV)\)。
初始条件
当选择 \(0\) 个物品时,无论总体积为多少,总价值都是 \(0\),故
最终结果
最终应当是 从前 \(n\) 个物品中选,总体积不超过 \(V\) 的方案中的最大价值,即
代码实现
#include <bits/stdc++.h>
const int N = 1e3 + 10;
int n, V, f[N];
int main() {
std::cin >> n >> V;
for (int i = 1, v, w; i <= n; ++i) {
std::cin >> v >> w;
for (int j = V; j >= v; --j) // 使用上一层的,倒序遍历
f[j] = std::max(f[j], f[j - v] + w);
}
std::cout << f[V] << std::endl;
return 0;
}
完全背包
题目描述
有 \(n\) 个物品,一个体积为 \(V\) 的背包。
第 \(i\) 个物品体积为 \(v_i\),价值为 \(w_i\)。
每个物品可以选择无限次,最大化放入背包物品的总价值。
输出最大总价值。
状态表示
集合
令 \(f_{i,j}\) 表示 从前 \(i\) 个物品中选,总体积不超过 \(j\) 的方案集合。
属性
集合中的 最大价值。
状态转移
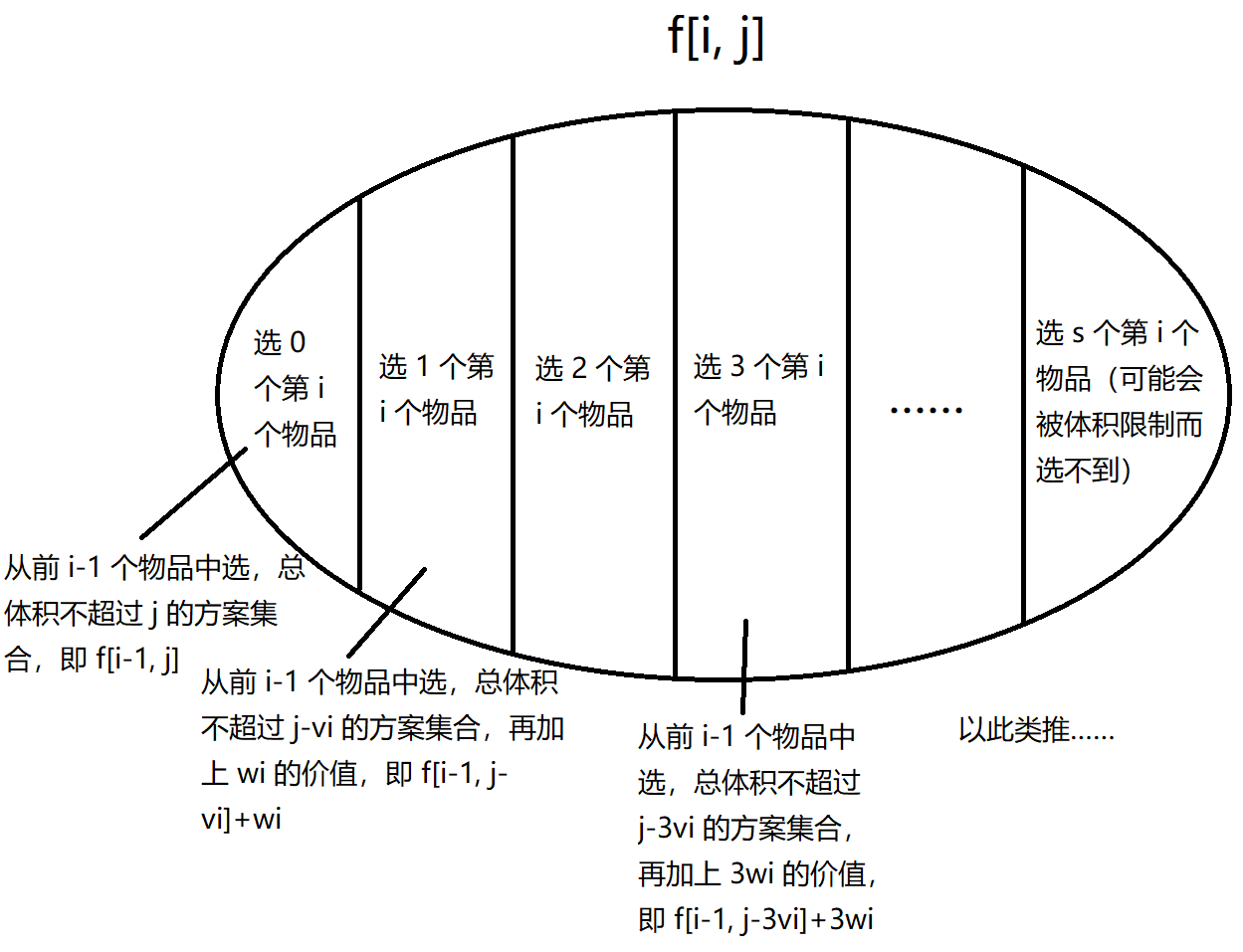
这样 DP 的时间复杂度是 \(O(nV^2)\) 的,有没有优化方法呢?
可以发现
故
此时时间复杂度降为 \(O(nV)\)。
初始条件
当选择 \(0\) 个物品时,无论总体积为多少,总价值都是 \(0\),故
最终结果
最终应当是 从前 \(n\) 个物品中选,总体积不超过 \(V\) 的方案中的最大价值,即
代码实现
#include <bits/stdc++.h>
const int N = 1e3 + 10;
int n, V, f[N];
int main() {
std::cin >> n >> V;
for (int i = 1, v, w; i <= n; ++i) {
std::cin >> v >> w;
for (int j = v; j <= V; ++j) // 使用同一层的,正序遍历
f[j] = std::max(f[j], f[j - v] + w);
}
std::cout << f[V] << std::endl;
return 0;
}
多重背包
题目描述
朴素算法
状态表示
有 \(n\) 种物品,一个体积为 \(V\) 的背包。
第 \(i\) 个物品体积为 \(v_i\),价值为 \(w_i\)。
每个物品可以选择 \(s_i\) 次,最大化放入背包物品的总价值。
输出最大总价值。
集合
令 \(f_{i,j}\) 表示 从前 \(i\) 种物品中选,总体积不超过 \(j\) 的方案集合。
属性
集合中的 最大价值。
状态转移
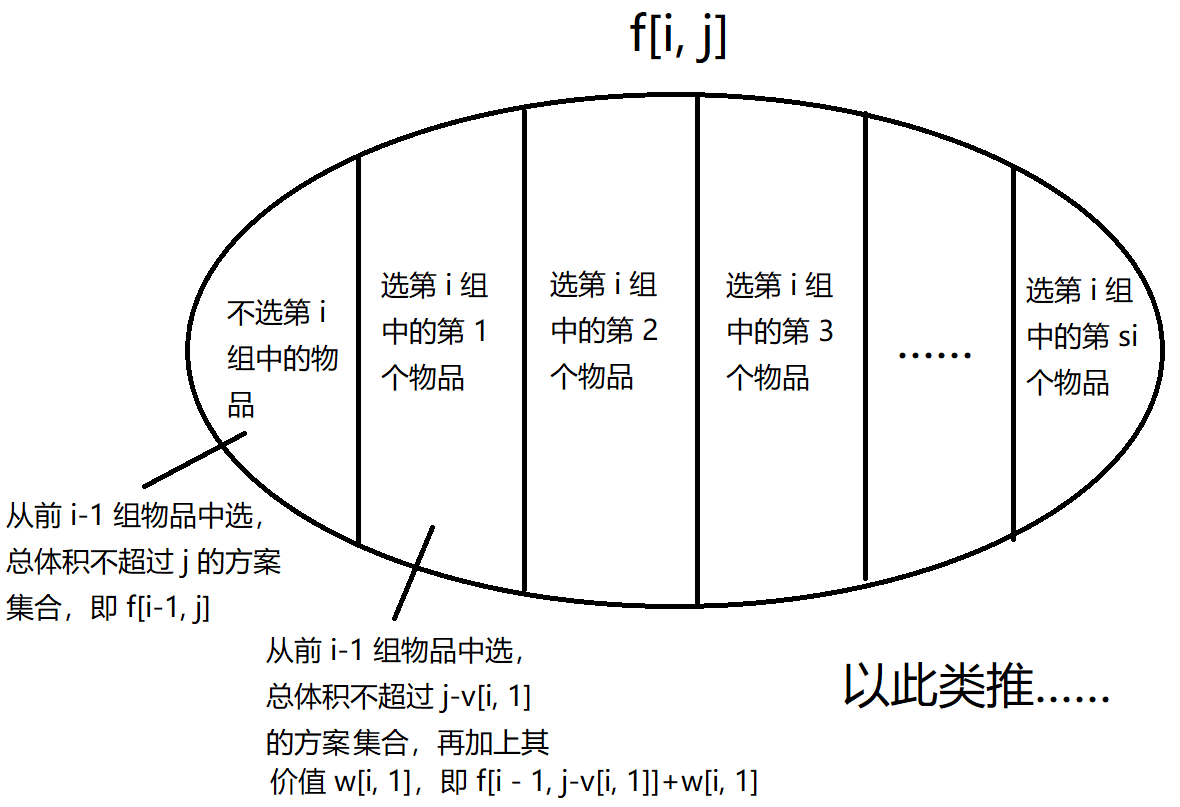
故
初始条件
当选择 \(0\) 个物品时,无论总体积为多少,总价值都是 \(0\),故
最终结果
最终应当是 从前 \(n\) 种物品中选,总体积不超过 \(V\) 的方案中的最大价值,即
代码实现
#include <bits/stdc++.h>
const int N = 110;
int n, V, f[N];
int main() {
std::cin >> n >> V;
for (int i = 1, v, w, s; i <= n; ++i) {
std::cin >> v >> w >> s;
for (int j = V; ~j; --j) // 一定要把 j 放在外面!使用上一层的,倒序遍历
for (int k = 0; k <= s && k * v <= j; ++k)
f[j] = std::max(f[j], f[j - k * v] + k * w);
}
std::cout << f[V] << std::endl;
return 0;
}
二进制优化
引理:
\(\forall\,n\in\mathbb{N^{*}}\),\(n\) 可以分解为 \(2^0,2^1,\cdots,2^k,s(2^0+2^1+\cdots+2^k+s=n,s\in[0,2^{k+1})\)。这些数能且仅能凑出 \([0,n]\) 中的整数。
证明:
显然地,\(2^0,2^1,\cdots,2^k\) 可以凑出 \([0,2^{k+1}-1]\) 之间的所有正整数。
将其中每个数 \(+s\),则可以凑出 \([s,n]\) 之间的所有正整数。
因为 \(s\le2^{k+1}-1\),所以 \([0,2^{k+1}-1]\cup[s,n]=[0,n]\)。
证毕。
对于每种物品的个数 \(s\),我们也可以按照这样的方法拆分,做 01 背包。
代码实现
#include <bits/stdc++.h>
const int N = 2e3 + 10;
int n, V, f[N];
int main() {
std::cin >> n >> V;
for (int i = 1, v, w, s; i <= n; ++i) {
std::cin >> v >> w >> s;
for (int k = 1; k <= s; k <<= 1) {
for (int j = V; j >= k * v; --j) // 使用上一层的,倒序遍历
f[j] = std::max(f[j], f[j - k * v] + k * w);
s -= k;
}
if (s)
for (int j = V; j >= s * v; --j)
f[j] = std::max(f[j], f[j - s * v] + s * w);
}
std::cout << f[V] << std::endl;
return 0;
}
单调队列优化
在朴素算法中,状态转移方程如下:
容易发现,\(\{f_j,f_{j-v},f_{j-2v},\cdots,f_{j-sv}\}\subset\bar{j}(\bmod v)\),即这些数同属一个模 \(m\) 的同余系。
不同同余系之间不相干,所以我们可以在一个同余系内考虑。
可以发现,求 \(f_j\) 其实就是求一段长度为 \(s\) 的区间的最大值,故考虑使用单调队列。
令非负整数 \(q\in[0,v)\),可得如下式子:
上面的最后一个式子只是理想情况,可能取不到 \(f_q\)。
可以发现在第 \(1\) 个式子中是 \(f_q\),第 \(2\) 个式子中是 \(f_q+w\),最后一个式子中为 \(f_q+pw\)。队列中的值都在变化,是无法使用单调队列的。
怎么办呢?
其实可以把 \(\max\) 中的 \(w\) 都提出来,得到如下式子:
此时队列中原有的元素就不会发生变化了。
虽然在单调队列中插入的只是下标(如 \(q,q+v,\cdots,q+pv\)),但是这个下标 \(r\) 所代表的值 \(\operatorname{val}(r)\) 为多少呢?
假设 \(r=m+nv\)。
通过观察可以发现,\(w\) 的系数就是 \(n\),故:
有了 \(\operatorname{val}(r)\),就可以解决当前元素插入单调队列队尾的问题了。
然后我们要解决如何判断队头是否过时的问题。
假设当前队头 \(a=j+xv\),当前的体积 \(b=j+yv(x<y)\)。
容易发现,当 \(y-x>s\) 时,队头就失效了。
又因为 \(b-a=(y-x)v\),所以队头失效的条件为:
最后,我们应该知道如何用单调队列队头 \(a\) 来更新 \(f_b\)。
朴素式子中第 \(2\) 项以以后的元素都是在单调队列中的,所以后面这些值的 \(\max\) 相当于 \(\operatorname{val}(a)\)。
因为 \(b=j+yv\),所以 \(\max\) 外的 \(w\) 的系数为 \(y=\dfrac{b-j}{v}\)。
故可得:
此时就可以 \(O(1)\) 计算 \(f_b\) 了。
该算法时间复杂度为 \(O(nV)\)。
代码实现
PS:具体实现时,如果只开一个一维数组,那么就应当倒序循环。但是如果倒序循环,单调队列就无法优化。所以应该采用滚动数组技巧。此处使用 \(f\) 存储这一层,\(g\) 存储上一层。
#include <bits/stdc++.h>
const int N = 2e4 + 10;
int n, V, f[N], g[N], q[N]; // f,g 为 DP 数组,q 为单调队列(最大容量为 V)
int main() {
std::cin >> n >> V;
for (int i = 1, v, w, s; i <= n; ++i) {
std::cin >> v >> w >> s;
memcpy(g, f, sizeof(f)); // g <- f
for (int j = 0; j < v; ++j) { // 枚举同余类
int hh = 0, tt = -1; // 单调队列的头和尾
for (int k = j; k <= V; k += v) { // 在同一个同余类内枚举体积
while (hh <= tt && k - q[hh] > s * v) ++hh; // 弹出队头
if (hh <= tt) f[k] = std::max(g[k], g[q[hh]] + (k - q[hh]) / v * w); // 状态转移
while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) --tt; // 弹出队尾
q[++tt] = k; // 插入当前元素
}
}
}
std::cout << f[V] << std::endl;
return 0;
}
混合背包
题目描述
有 \(n\) 种物品,一个体积为 \(V\) 的背包。
物品一共有三类:
- 第一类物品只能用 \(1\) 次;
- 第二类物品可以用无限次;
- 第三类物品最多只能用 \(s_i\) 次。
第 \(i\) 种物品,体积为 \(v_i\),价值为 \(w_i\)。
最大化放入背包物品的总价值,并输出最大总价值。
解决方法
01 背包、完全背包、多重背包的混合版。
可以分类讨论:
- 对于完全背包,可以单独计算
- 对于 01 背包,当成 \(s_i=1\) 的多重背包,和多重背包一起计算。
代码实现
#include <bits/stdc++.h>
const int N = 1e3 + 10;
int n, V, f[N];
int main() {
std::cin >> n >> V;
for (int i = 1, v, w, s; i <= n; ++i) {
std::cin >> v >> w >> s; // 本题中 s=-1 为第一类,s=0 为第二类,s 是正整数为第三类
if (!s) { // 完全背包
for (int j = v; j <= V; ++j)
f[j] = std::max(f[j], f[j - v] + w);
} else {
if (s == -1) s = 1; // 01 背包->多重背包
for (int k = 1; k <= s; k <<= 1) {
for (int j = V; j >= k * v; --j)
f[j] = std::max(f[j], f[j - k * v] + k * w);
s -= k;
}
if (s)
for (int j = V; j >= s * v; --j)
f[j] = std::max(f[j], f[j - s * v] + s * w);
}
}
std::cout << f[V] << std::endl;
return 0;
}
分组背包
题目描述
有 \(n\) 组物品,一个体积为 \(V\) 的背包。
第 \(i\) 组物品有 \(s_i\) 个,同一组内的物品最多只能选一个。
第 \(i\) 组内的第 \(j\) 个物品,体积为 \(v_{i,j}\),价值为 \(w_{i,j}\)。
最大化放入背包物品的总价值,并输出最大总价值。
状态表示
集合
令 \(f_{i,j}\) 表示 从前 \(i\) 组物品中选,总体积不超过 \(j\) 的方案集合。
属性
集合中的 最大价值。
状态转移
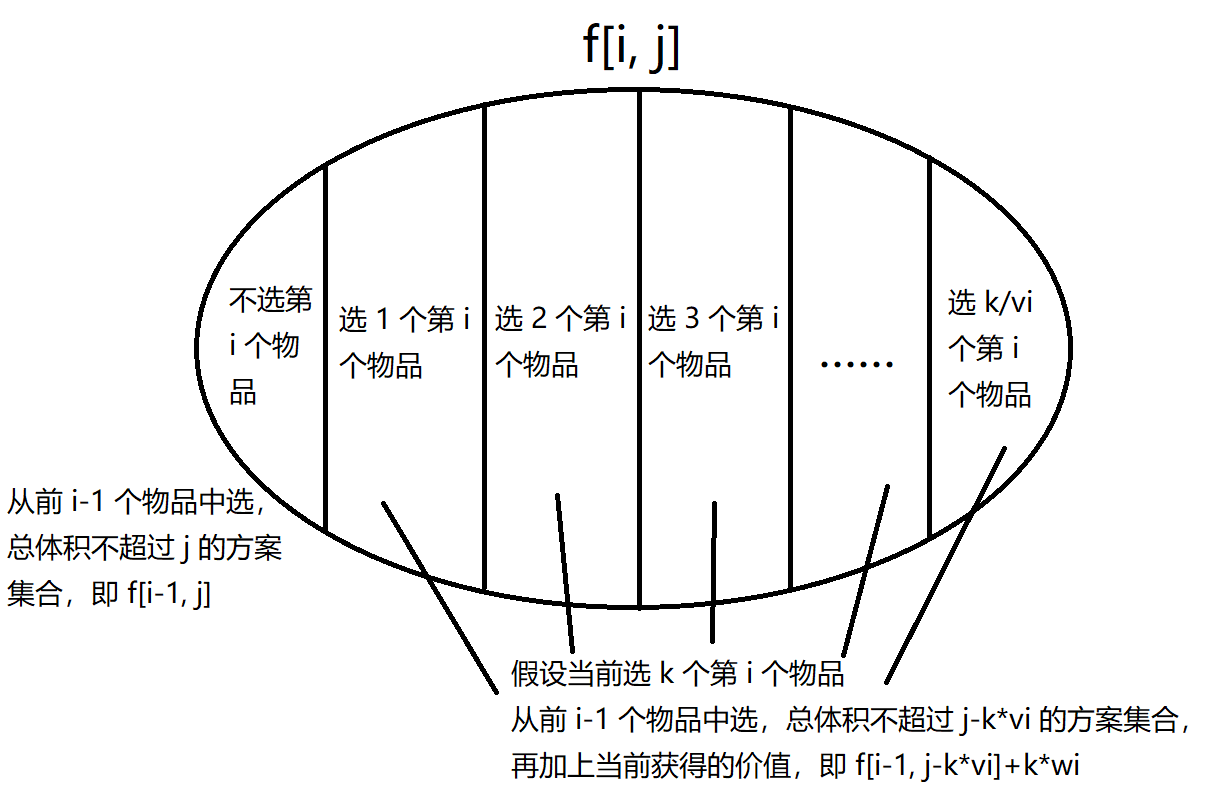
故
初始条件
当从前 \(0\) 组物品中选择时,无论总体积为多少,总价值都是 \(0\),故
最终结果
最终应当是 从前 \(n\) 组物品中选,总体积不超过 \(V\) 的方案中的最大价值,即
代码实现
#include <bits/stdc++.h>
const int N = 110; // 假设 V,s[i] 同阶
int n, V, v[N], w[N], f[N];
int main() {
std::cin >> n >> V;
for (int i = 1, s; i <= n; ++i) {
std::cin >> s;
for (int j = 1; j <= s; ++j) std::cin >> v[j] >> w[j];
for (int j = V; ~j; --j)
for (int k = 1; k <= s; ++k)
if (j >= v[k]) f[j] = std::max(f[j], f[j - v[k]] + w[k]);
}
std::cout << f[V] << std::endl;
return 0;
}
二维费用背包
题目描述
有 \(n\) 组物品,一个体积为 \(V\),最大承重为 \(M\) 的背包。
第 \(i\) 个物品体积为 \(v_i\),重量为 \(m_i\),价值为 \(w_i\)。
每个物品只能选择一次,最大化放入背包物品的总价值。
输出最大总价值。
状态表示
集合
令 \(f_{i,j,k}\) 表示 从前 \(i\) 个物品中选,总体积不超过 \(j\),总重量不超过 \(k\) 的方案集合。
属性
集合中的 最大价值。
状态转移
与 01 背包类似,分选择和不选两种情况。
故
初始条件
当选择 \(0\) 个物品时,无论总体积、总重量为多少,总价值都是 \(0\),故
最终结果
最终应当是 从前 \(n\) 个物品中选,总体积不超过 \(V\),总重量不超过 \(M\) 的方案中的最大价值,即
代码实现
#include <iostream>
const int N = 1e2 + 10;
int n, V, M, f[N][N];
int main() {
std::cin >> n >> V >> M;
for (int i = 1, v, m, w; i <= n; ++i) {
std::cin >> v >> m >> w;
for (int j = V; j >= v; --j)
for (int k = M; k >= m; --k)
f[j][k] = std::max(f[j][k], f[j - v][k - m] + w);
}
std::cout << f[V][M] << std::endl;
return 0;
}
有依赖的背包问题
题目描述
有 \(n\) 个物品和一个体积为 \(V\) 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
第 \(i\) 个物品体积为 \(v_i\),价值为 \(w_i\),依赖的父结点编号为 \(p_i\)。若 \(p_i=-1\),则表示根节点。
求解将哪些物品装入背包,可使物品总体积不超过背包体积,且总价值最大。
输出最大价值。
方法一:\(O(nV^2)\)
状态表示
集合
令 \(f_{u,j}\) 表示 在以 \(u\) 为根结点的子树中(包含 \(u\)),总体积不超过 \(j\) 的方案集合。
属性
集合中的 最大价值。
状态转移
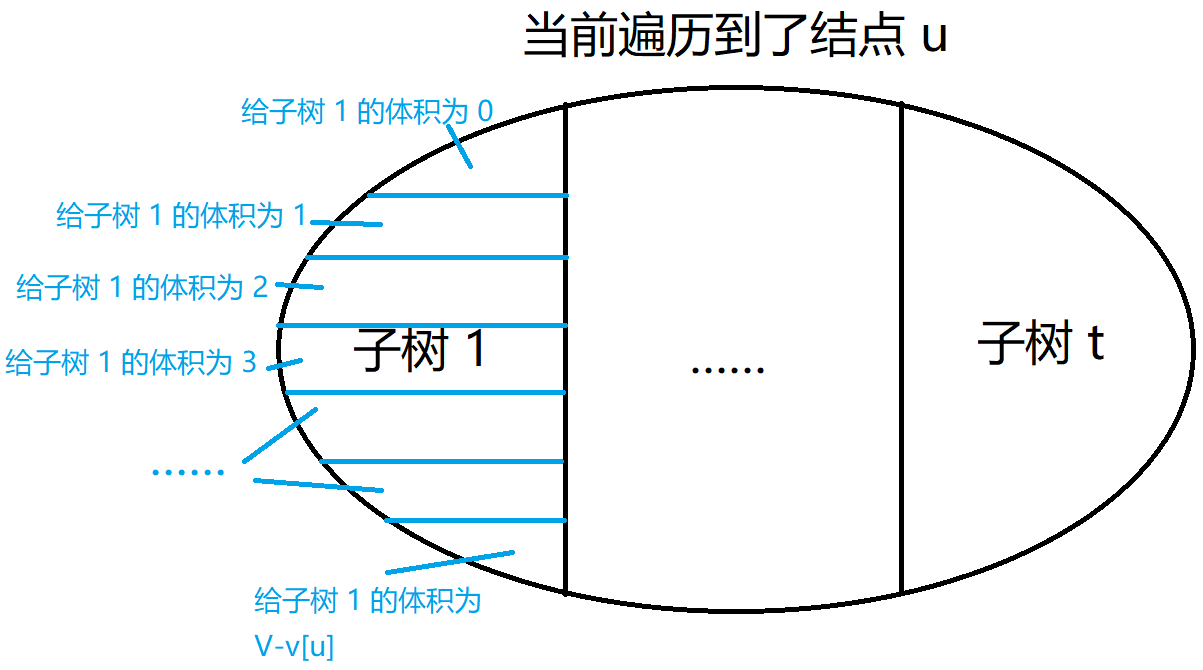
对于每个儿子,可以用体积划分集合。
由于每个儿子只能有一种体积,所以相当于一个分组背包。
时间复杂度为 \(O(nV^2)\)。
初始条件
最终结果
最终结果应为在根结点的子树中,总体积不超过 \(V\) 的方案集合,即
\(\text{root}\) 为树的根结点。
代码实现
#include <bits/stdc++.h>
const int N = 110;
std::vector<int> g[N];
int n, V, root, v[N], w[N], f[N][N];
void dp(int u) {
for (auto son : g[u]) { // 遍历儿子
dp(son);
for (int j = V - v[u]; ~j; --j) // 由于一定要包含 u 结点,所以最大体积为 V-v[u]
for (int k = 0; k <= j; ++k)
f[u][j] = std::max(f[u][j], f[u][j - k] + f[son][k]);
}
for (int i = V; i >= v[u]; --i) f[u][i] = f[u][i - v[u]] + w[u]; // 加入 u,更新
for (int i = 0; i < v[u]; ++i) f[u][i] = 0; // 不可能的情况
}
int main() {
std::cin >> n >> V;
for (int i = 1, p; i <= n; ++i) {
std::cin >> v[i] >> w[i] >> p;
if (p == -1) root = i;
else g[p].push_back(i);
}
dp(root);
std::cout << f[root][V] << std::endl;
return 0;
}
方法二:\(O(nV)\)
对于树上问题,考虑转成欧拉序进行处理。
下记得到的欧拉序为 \(\{\text{euler}\}\),结点 \(u\) 第一次出现为 \(\operatorname{in}(u)\),第二次出现为 \(\operatorname{out}(u)\)。
令 \(f_{i,j}\) 表示考虑欧拉序的后缀 \([i,2n]\) 时,对于容量为 \(j\) 的背包可以获得的最大价值。
初始化
当 \([i,2n]\) 表示空区间,即 \(i>2n\) 时,答案显然为 \(0\)。
故
状态转移
根据状态定义,遍历 \(i\) 从 \(2n\) 到 \(1\)。
对于当前的位置 \(i\),记 \(u=\text{euler}_i\),即当前结点的编号。
分讨。
遇到出口
此时 \(i=\operatorname{out}(u)\),说明 \(u\) 及其子树决策已经结束了,不代表一个可以放进背包的物品。
那么 \([i,2n]\) 的价值就等价于 \([i+1,2n]\) 的价值,故
遇到入口
此时 \(i=\operatorname{in}(u)\),是我们的重头戏。
再分讨一下:
-
不选择物品 \(u\):
如果我们不选择 \(u\),那么整个子树(即欧拉序中 \([\operatorname{in}(u),\operatorname{out}(u)]\))都不能选择,那么
\[f_{i,j}=f_{\operatorname{out}(u)+1,j} \] -
选择物品 \(u\):
注意,该情况的存在条件为 \(j\ge v_u\)(此处记体积为 \(\{v\}\),价值为 \(\{w\}\))。
我们将 \(u\) 放入后,剩余体积为 \(j-v_u\),获得价值为 \(w_u\)。
剩下来的容量,可以在后续的结点中分配,由于后续结点为 \([i+1,2n]\)(相当于 \([\operatorname{in}(u)+1,2n]\)),故
\[f_{i,j}=f_{i+1,j-v_u}+w_u \]
两种情况取一个 \(\max\) 即可。
时间复杂度。
- 构造欧拉序 \(O(n)\)。
- 遍历复杂度 \(O(n)\),内部对于遇到入口时为 \(O(V)\),故 DP 的时间复杂度为 \(O(nV)\)。
综上,时间复杂度为 \(O(nV)\)。
代码实现
注意要开两倍数组!
#include <bits/stdc++.h>
const int N = 2e2 + 10;
std::vector<int> g[N];
int n, V, root, v[N], w[N];
int f[N][N];
int cnt, euler[N], in[N], out[N];
void input() {
std::cin >> n >> V;
for (int i = 1, p; i <= n; ++i) {
std::cin >> v[i] >> w[i] >> p;
if (p == -1) root = i;
else g[p].push_back(i);
}
}
void dfs(int u) {
euler[++cnt] = u, in[u] = cnt;
for (auto v : g[u]) dfs(v);
euler[++cnt] = u, out[u] = cnt;
}
void dp() {
for (int i = cnt; i; --i) {
int u = euler[i];
if (i == out[u]) for (int j = 0; j <= V; ++j) f[i][j] = f[i + 1][j]; // 遇到出口
else { // 遇到入口
for (int j = 0; j <= V; ++j) {
f[i][j] = f[out[u] + 1][j]; // 不选 u
if (j >= v[u]) f[i][j] = std::max(f[i][j], f[i + 1][j - v[u]] + w[u]); // 选 u
}
}
}
}
int main() {
input();
dfs(root); // 构建欧拉序
dp();
std::cout << f[1][V] << std::endl; // 由定义容易得到
return 0;
}
背包问题求方案数
题目描述
有 \(n\) 件物品,体积为 \(V\) 的背包。
第 \(i\) 件物品体积为 \(v_i\),价值为 \(w_i\),每件物品只能用一次。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包体积,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 \(10^9+7\) 的结果。
状态表示
集合
令 \(f_{i,j}\) 表示从前 \(i\) 个物品中选,总体积 恰好 为 \(j\) 的方案集合。
属性
集合中的 最大价值。
状态转移
令 \(g_{i,j}\) 表示到达 \(f_{i,j}\) 的方案数。
可以知道,
可以分三类讨论:
- \(f_{i-1,j}>f_{i-1,j-v_i}+w_i\):此时 \(f_{i,j}\gets f_{i-1,j}\)。那么 \(g_{i,j}\gets g_{i-1,j}\)。
- \(f_{i-1,j} < f_{i-1,j-v_i}+w_i\):此时 \(f_{i,j}\gets f_{i-1,j-v_i}+w_i\)。那么 \(g_{i,j}\gets g_{i-1,j-v}\)。
- \(f_{i-1,j} = f_{i-1,j-v_i}+w_i\):此时两种前置情况都可以到达 \(f_i,j\)。那么 \(g_{i,j}\gets g_{i-1,j}+g_{i-1,j-v}\)。
初始条件
由于 \(f_{i,j}\) 表示 恰好 总体积为 \(j\) 的方案集合,那么
最终结果
令 \(k\) 表示背包中的最大总价值,即 \(f\) 中的最大值。此时答案为:
代码实现
#include <bits/stdc++.h>
const int N = 1e3 + 10;
const int MOD = 1e9 + 7;
int n, V, ans, cnt, f[N], g[N];
int main() {
std::cin >> n >> V;
memset(f, -0x3f, sizeof(f));
f[0] = 0, g[0] = 1;
for (int i = 1, v, w; i <= n; ++i) {
std::cin >> v >> w;
for (int j = V; j >= v; --j) {
int mx = std::max(f[j], f[j - v] + w), s = 0;
if (mx == f[j]) s = g[j];
if (mx == f[j - v] + w) (s += g[j - v]) %= MOD;
f[j] = mx, g[j] = s;
}
}
ans = *std::max_element(f, f + V + 1);
for (int i = 0; i <= V; ++i)
if (f[i] == ans) cnt += g[i];
std::cout << cnt << std::endl;
return 0;
}
背包问题求具体方案
题目描述
有 \(n\) 件物品和一个体积为 \(V\) 的背包。
第 \(i\) 件物品体积为 \(v_i\),价值为 \(w_i\),每件物品只能用一次。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包体积,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。
状态表示
集合
令 \(f_{i,j}\) 表示从后 \(n-i+1\) 件物品中选,总体积不超过 \(j\) 的方案集合(至于为什么要这样,见下文)。
属性
集合中的最大价值。
状态转移
容易知道,
初始条件
获得方案
题目要求输出 字典序最小的方案。从前往后考虑,每个物品必然是 能选就选。
如何知道第 \(i\) 个物品能不能选呢?
可以看 \(f_{i,j}\) 是否从选第 \(i\) 个物品的情况转移过来(如果 \(f_{i+1,j}=f_{i+1,j-v_i}+w_i\),根据能选就选的原则,也得选)
Q:为什么要这样定义 \(f_{i,j}\)?
A:倒着定义,\(f_{1,V}\) 就是全局最优解。根据转移的情况来向后推,\(f_{2,\Delta V},f_{2,\Delta V'},\cdots\) 都是全局最优解,保证输出结果是全局最优方案。但是如果正着定义,\(f_{1,V}\) 是局部最优解,在后面的转移中可能没有入选,会导致输出结果不是全局最优方案。
提供一组数据:
输入
4 5 1 2 2 4 3 4 4 6输出 1(倒着定义)
1 4输出 2(正着定义)
1 2可以发现输出 2 只是纯粹的能选就选,没有考虑全局情况。
(这里可能解释不清楚,轻喷/kk)
详见代码。
代码实现
#include <bits/stdc++.h>
const int N = 1e3 + 10; // 假设 n,V 同阶
int n, V, v[N], w[N], f[N][N]; // 此时不能压成一维了
int main() {
std::cin >> n >> V;
for (int i = 1; i <= n; ++i) std::cin >> v[i] >> w[i];
for (int i = n; i; --i)
for (int j = 0; j <= V; ++j) {
f[i][j] = f[i + 1][j];
if (j >= v[i]) f[i][j] = std::max(f[i][j], f[i + 1][j - v[i]] + w[i]);
}
int j = V; // 剩余空间的体积
for (int i = 1; i <= n; ++i) {
if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) { // 从选第 i 个的情况转移过来
std::cout << i << " ";
j -= v[i];
}
}
std::cout << std::endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号