循环神经网络个人理解

之前讲过CNN和BP，循环神经网络与前两个网络结构有部分区别。

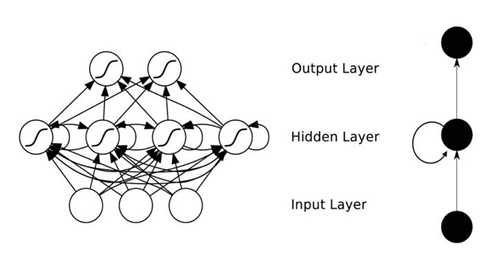
这是循环神经网络的基本结构

区别在于：从结构上来看卷积神经网络层与层之间是全连接的，且同一层之间神经元无连接，而循环神经网络层与层之间有连接。另外，循环神经网络适合处理序列数据。

 RNNs的目的使用来处理序列数据。在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNNs之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。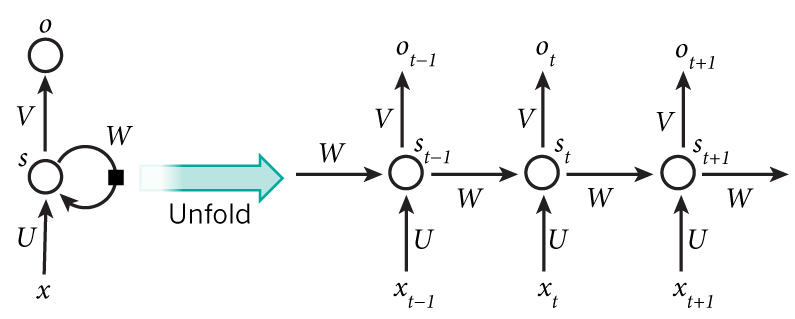

如图所示，有多个输入以及多个输出，循环神经网络适合处理时间序列数据，比如文本预测墩、自然语言处理等。在输入的不同文字中，根据模型训练，得出一定权重，并且根据训练结果来进行预测。比如输入我喜欢学习数学，他会根据每一时刻历史数据以及词性形式来进行预测，输入多种类似的文字，他就会根据你的历史输入来进行预测，从而达到文本预测的效果。同一隐藏层设置路径可以使得历史信息也能让下一层接收，从而做出更好的预测。

前向传播流程： 假设激活函数为$$\sigma $$ $$s_{}^{t}=s_{}^{t-1}*W+x_{}^{t}*U$$ $$y_{}^{t}=\sigma (s_{}^{t})$$ $$o_{}^{t}=y_{}^{t}*v$$ 定义t时刻损失： $$E_{}^{t}=-y_{}^{t}log(o_{}^{t})$$ 总体损失： $$E=\sum_{1}^{t_{}^{e}}L_{}^{t}$$ 其中W、U、V都是在每一个输出单元中其权值相同，相当于整个网络就只需要这三个权值，这极大的减少了训练参数量。 同时，RNN的调整参数中，同样使用反向传播算法，不过这个反向传播叫BPTT（BP through time）。RNN有记忆功能，其输出依赖输入。同时，由于整个网络就这三个权重（3层网络），所以要改变权值时，需要用链式法则依次迭代到最早输出结点的那个权值。

 

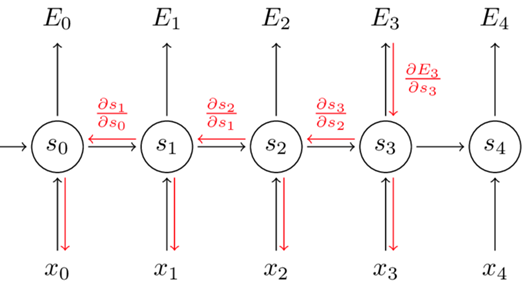
假设我们求 $$E_{}^{3}$$对v的偏导，这个相对好求，因为v的下一步就是$$E_{}^{3}$$ 于是： $$\frac{\partial E_{}^{3}}{\partial v}=\frac{\partial E_{}^{3}}{\partial y_{}^{3}}*\frac{\partial y_{}^{3}}{\partial s_{}^{3}}*\frac{\partial s_{}^{3}}{\partial v}$$ 假设某个输出结点要对w求偏导，他需要从该输出结点开始求，并一直迭代到最初那个结点。 假设我们求$$\frac{\partial E_{}^{3}}{\partial w}$$ 我们需要一层一层的求，即 $$\frac{\partial E_{}^{3}}{\partial W}=\frac{\partial E_{}^{3}}{\partial y_{}^{3}}*\frac{\partial y_{}^{3}}{\partial s_{}^{3}}*\frac{\partial s_{}^{3}}{\partial W}$$ 而 $$\frac{\partial s_{}^{3}}{\partial W}=\frac{\partial s_{}^{3}}{\partial y_{}^{2}}*\frac{\partial y_{}^{2}}{\partial s_{}^{2}}*\frac{\partial s_{}^{2}}{\partial y_{}^{1}}*\frac{\partial y_{}^{1}}{\partial s_{}^{1}}*\frac{\partial s_{}^{1}}{\partial y_{}^{0}}*\frac{\partial y_{}^{0}}{\partial s_{}^{0}}*\frac{\partial s_{}^{0}}{\partial w}$$ 最终得出结论： $$\frac{\partial E_{}^{3}}{\partial W}=\sum_{k=0}^{3} \frac{\partial E_{}^{3}}{\partial y_{}^{3}}*\frac{\partial y_{}^{3}}{\partial s_{}^{3}}*\frac{\partial s_{}^{3}}{\partial s_{}^{k}}*\frac{\partial s_{}^{k}}{\partial w}$$ 可能有人疑惑为什么变成求和的符号？ 我们可以看出来 $$s_{}^{2}=\sigma (y_{}^{1}*w+u*x_{}^{2})$$ 在对w求偏导的过程中，上述式子中 $$y_{}^{1}里面也包含w，而y_{}^{1}又*w，在对其求偏导的过程中出现（y_{}^{1}+\frac{\partial y_{}^{1}}{\partial w}）的情况$$ 因此出现加号求和，从而得出上述结论。 同理可得： $$\frac{\partial E_{}^{3}}{\partial u}=\sum_{k=0}^{3}\frac{\partial E_{}^{3}}{\partial y_{}^{3}}*\frac{\partial y_{}^{3}}{\partial s_{}^{3}}*\frac{\partial s_{}^{3}}{\partial s_{}^{k}}*\frac{\partial s_{}^{3}}{\partial u}$$ 上述只是对某一时刻的误差求偏导，若要改变总体的参数，则需把每个L的误差都求出来并且求和，得出最终结果，即： $$\frac{\partial E}{\partial v}=\sum_{t=0}^{}\frac{\partial E_{}^{t}}{\partial v}$$ $$\frac{\partial E}{\partial w}=\sum_{t=0}^{}\frac{\partial E_{}^{t}}{\partial w}$$ $$\frac{\partial E}{\partial u}=\sum_{t=0}^{}\frac{\partial E_{}^{t}}{\partial u}$$ 参考： [1]BPTT-RNN训练算法 https://blog.csdn.net/caihuanqia/article/details/106745947