卷积神经网络

对于卷积神经网络，本文将从卷积神经网络的简介、前向传播、卷积核、、特性、反向传播这五个方面进行讲解。

简介

卷积神经网络（Convolutional Neural Network,CNN或ConvNet）是一种带有卷积结构的深度神经网络。由一个或多个卷积层、池化层以及全连接层等组成。与其他深度学习结构相比，卷积神经网络在图像等方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他浅层或深度神经网络，卷积神经网络需要考量的参数更少，使之成为一种颇具吸引力的深度学习结构。

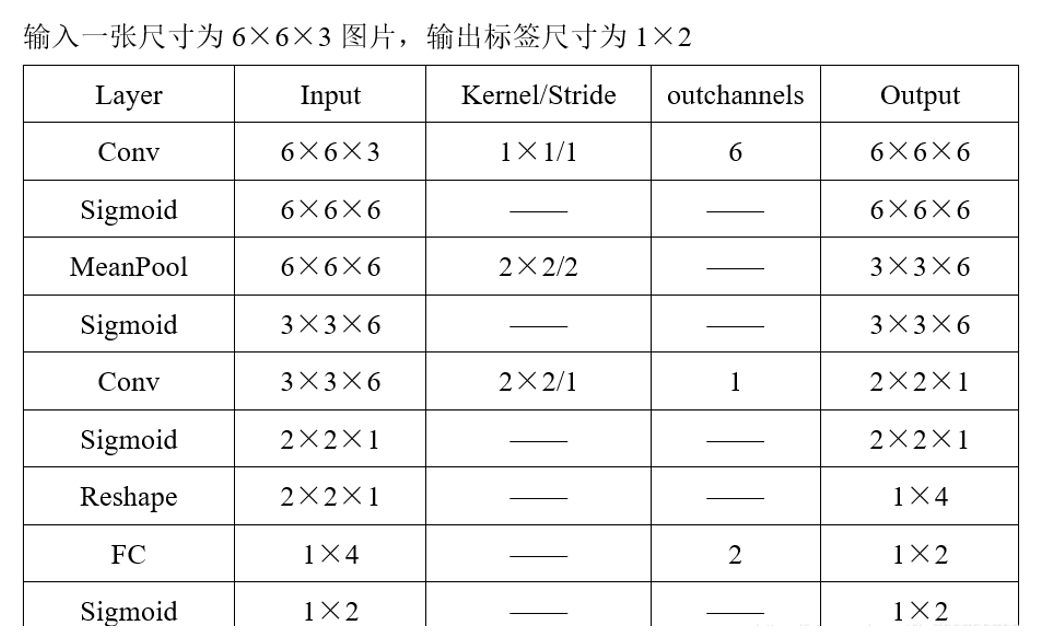
卷积神经网络结构包括：卷积层，(降采样层)池化层 ，全连接层。每一层有多个特征图，每个特征图通过一种卷积滤波器提取输入的一种特征，每个特征图有多个神经元。

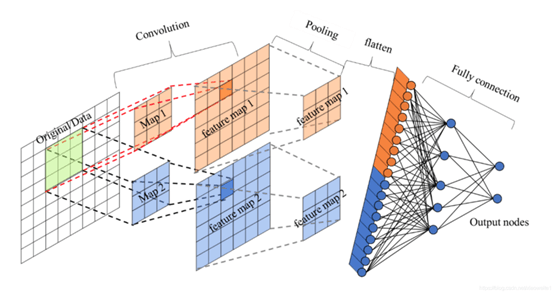
上图只是一个卷积神经网络的基本构成，其中卷积层和池化层可以根据实际情况任意增加。当前卷积神经网络的应用场合非常广泛，比如图像识别，自然语言处理，灾难性气候预测甚至围棋人工智能等，但是最主要的应用领域还是图像识别领域。

卷积的定义：

卷积、旋积或褶积(英语：Convolution)是通过两个函数f和g生成第三个函数的一种数学算子，表征函数f与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分。

一般定义函数f,g的卷积（f*g）(n)如下：

连续形式：

$$(f*g)(n)=\int_{-∞}^{+∞}f(x)g(n-x)dx$$

离散形式：

$$(f*g)(n)=\sum_{x=-∞}^{+∞}f(x)g(n-x)$$

卷积有两个典型的应用场景:

1.信号分析

一个输入信号f(t)经过一个线性系统（其特征可以用单位冲击响应函数g(t)描述）以后，输出信号应该是什么？实际上通过卷积运算就可以得到输出信号。

2.图像处理

输入一幅图像f(x,y)，经过特定设计的卷积核g(x,y)进行卷积处理以后，输出图像将会得到模糊，边缘强化等各种效果。

 

 

数学中的卷积，主要是为了诸如信号处理、求两个随机变量的分布而定义的运算，所以需要“翻转”(将滤波器翻转180度)是根据问题的需要而确定的。 卷积神经网络中的“卷积”，是为了提取图像特征，只借鉴了“加权求和”的特点。

 

 

 

图像卷积

对于一张一个 5 × 5 的图像，使输入图片, 将其转化为矩阵, 矩阵的元素为对应的像素值. 假设有用一个 3 × 3 的卷积核进行卷积，可得到一个 3 × 3 的特征图. 卷积核也称为滤波器(Filter).

 

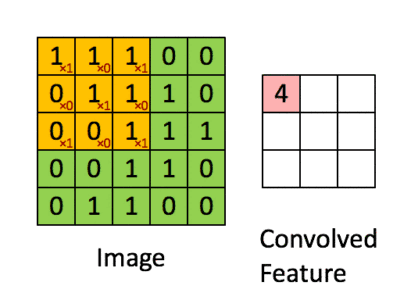
x1	x2	x3
x4	x5	x6
x7	x8	x9

*

w1	w2
w3	w4

+

b1	b2
b3	b4

=

p1	p2
p3	p4

 

 p₁=x₁*w₁+x₂*w₂+x₄*w₃+x₅*w₄₊b₁

  p₂=x2*w₁+x₃*w₂+x₅*w₃+x₆*w₄₊b₂

 p₃=x₄*w₁+x₅*w₂+x₇*w₃+x₈*w₄₊b₃

 p₄=x₅*w₁+x₆*w₂+x₈*w₃+x₉*w₄₊b₄

一般情况下, 输入的图片矩阵以及后面的卷积核, 特征图矩阵都是方阵, 这里设输入矩阵大小为 w, 卷积核大小为 k, 步幅为 s, 补零层数为 p, 则卷积后产生的特征图大小计算公式为:w ′ = ( w + 2 p − k ) /s + 1

卷积层(Convolutional Layer)：因为通过卷积运算我们可以提取出图像的特征，通过卷积运算可以使得原始信号的某些特征增强，并且降低噪声。用一个可训练的滤波器(矩阵)去卷积一个输入的图像（第一阶段是输入的图像，后面的阶段就是卷积特征map了），然后加一个偏置b，得到卷积层。

卷积操作其实可以分成三种操作：

(1)valid 操作，滑动步长为S，图片大小为 N₁*N₁，卷积核大小为N₂*N₂ ，卷积后图像大小：((N₁-N₂)/S+1)*(N₁-N₂)/S+1)

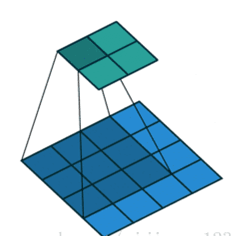
应用场景：可以用来缩小图像，减少参数

(2)same 操作，滑动步长为1，图片大小为N₁*N₁ ，卷积核大小为N₂*N₂ ，卷积后图像大小：N₁*N₁ 

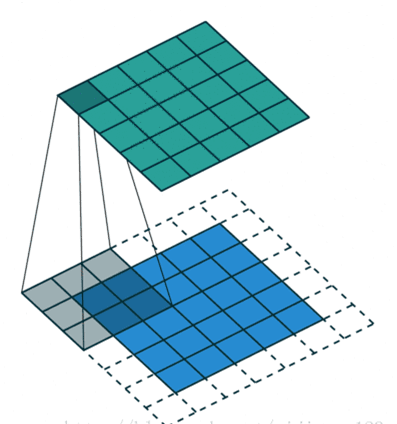
应用场景：这种模式可以在前向传播的过程中让特征图的大小保持不变（步幅为1的情况下），调参师不需要精准计算其尺寸变化(因为尺寸根本就没变化)，并且相对于valid卷积其对图像边缘的信息提取相对更完整。

(3)full 操作，滑动步长为1，图片大小为N₁*N₁ ，卷积核大小为N₂*N₂ ，卷积后图像大小：(N₁+N₂-1)*(N₁+N₂-1)

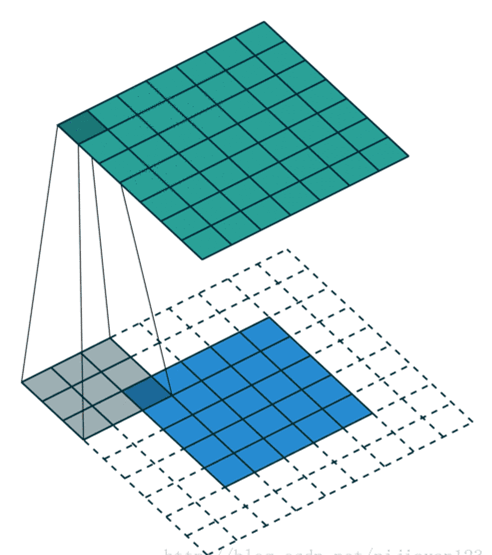
应用场景：主要为提供完整的边缘信息，让输入的图像信息与卷积核中每一元素都进行卷积计算，在步幅为1的情况下得出卷积后的矩阵要比初始矩阵大。

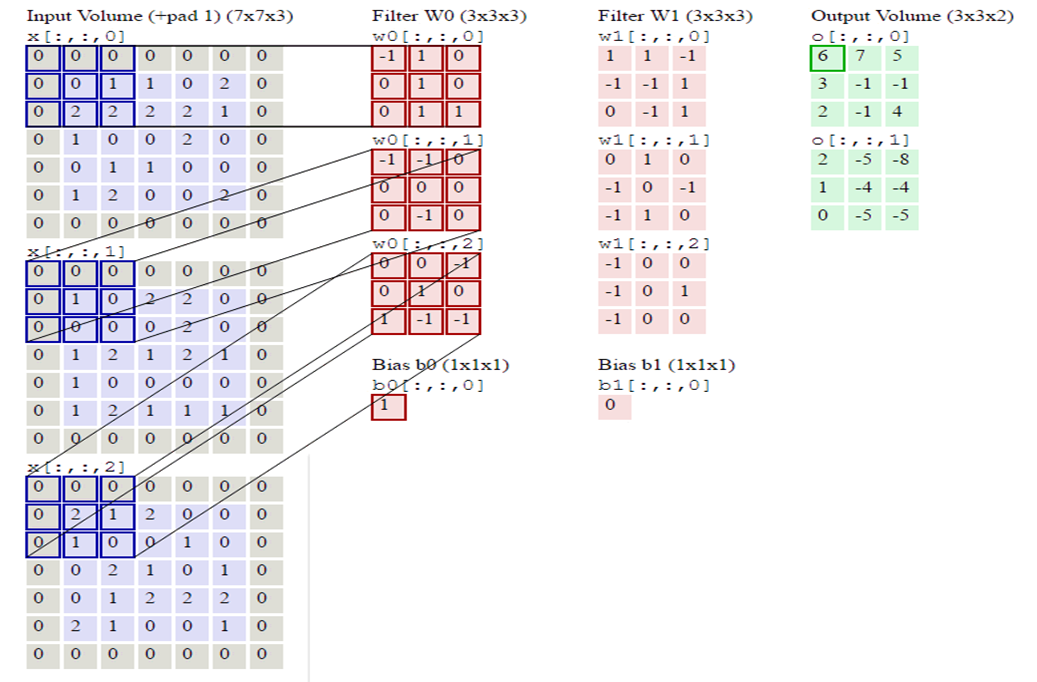
深度(Depth)

 深度就是卷积操作中用到的滤波器个数。这里对图片用了两个不同的滤波器，从而产生了两个特征映射。你可以认为这两个特征映射也是堆叠的2d矩阵，所以这里特征映射的“深度”就是2。

补零(Zero-padding)

边缘补零，对图像矩阵的边缘像素也施加滤波器。补零的好处是让我们可以控制特征映射的尺寸。补零也叫宽卷积，不补零就叫窄卷积。

步幅(Stride)

步幅是每次滑过的像素数。当Stride=2的时候每次就会滑过2个像素。步幅越大，特征映射越小。

常见卷积核：

1.拉普拉斯算子

0	-1	0
-1	4	-1
0	-1	0

 

就是将中心像素值复制4份，然后减去周围的4个像素值。在某点处的像素值如果与四周像素值都很接近，该处像素值肯定就“减”为接近于0。同样，在某点处的像素值如果与周围的像素值差别比较大，其更能扩大与周围像素值的大小，从而更为突出亮点。

举例：

初始矩阵

0	0	10	0	0
0	0	10	0	0
0	0	10	0	0
0	0	10	0	0
10	10	10	10	10

进行卷积操作结果：

-10	20	-10
-10	20	-10
-20	20	-20

 由于卷积时最下面的一行10卷积核未进行完全卷积，所以其特征提取不完全，但卷积结果还是反映出突出亮点的作用，中间一列与周围两列数值差距扩大。

周围补一层0进行卷积后的结果（相当于same操作）：

0	-10	30	-10	0
0	-10	20	-10	0
0	-10	20	-10	0
-10	-20	20	-20	-10
30	20	10	20	30

可以看出，相对于未补零的结果，其提取出来的特征更明显，最下面那一行的特征相对于valid操作可以更好的提取出来，同时也体现出突出亮点的作用。

在补一层o进行卷积的结果（相当于full操作）：

0	0	0	-10	0	0	0
0	0	-10	30	-10	0	0
0	0	-10	20	-10	0	0
0	0	-10	20	-10	0	0
0	-10	-20	20	-20	-10	0
-10	30	20	10	20	30	-10
0	-10	-10	-10	-10	-10	0

其卷积出来的结果更要完善一点，不过，由于输入矩阵数值较小，而且里面的数值也较小，可能一定程度上反映出来和same操作的结果特征差异不是那么明显，对于那种输入数值较大的矩阵，反应出来的差异可能会很明显。

下采样层（缩小图像）：也叫池化层(Pooling)。主要用于特征降维，压缩数据和参数数量，减小过拟合，提高模型的容错性，常用的有最大池化和平均池化。这和人的视觉系统是符合的，比如，人的注意力有时会集中色彩比较鲜明的区域而忽视其他不那么重要的区域。

和卷积一样, 池化也有一个滑动的核, 可以称之为滑动窗口, 该图中滑动窗口的大小为 2 × 2, 步幅为 2, 每滑动到一个区域, 则取最大值作为输出, 这样的操作称为 Max Pooling. 还可以采用输出均值的方式, 称为 Mean Pooling.

全连接层(fully connected layers，FC)：在卷积神经网络最后会加一个flatten层，将之前所得到的feature map“压平”，然后用一个全连接层输出最后的结果(卷积取的是局部特征，全连接就是把以前的局部特征重新通过权值矩阵组装成完整的图)，如果是分类的话，一般会利用softmax激活函数,最后就可以输出相应的分类结果了。

全连接层之前的作用是提取特征

全连接层的作用是分类

卷积神经网络的特性：

 

卷积神经网络有三个结构上的特性:局部连接、权重共享以及汇聚。和普通前馈神经网络相比，卷积神经网络的参数更少。

局部连接

局部连接会大大减少网络的参数。在处理图像这样的高维度输入时，让每个神经元都与前一层中的所有神经元进行全连接是不现实的。让每个神经元只与输入数据的一个局部区域连接，该连接的空间大小叫做神经元的感受野，它的尺寸是一个超参数，其实就是滤波器的空间尺寸。

 

 

 

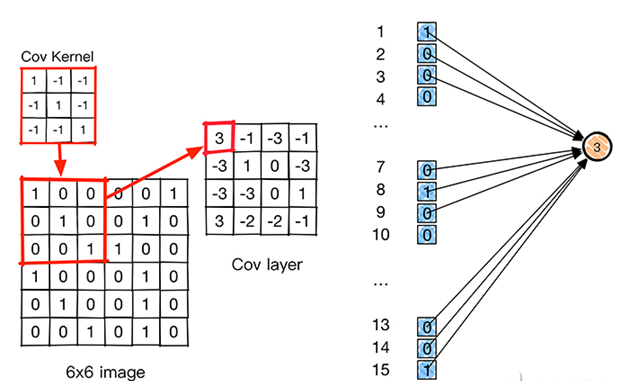
权值共享

从一个局部区域学习到的信息，应用到图像的其它地方去。即用一个相同的卷积核去卷积整幅图像，相当于对图像做一个全图滤波。一个卷积核对应的特征比如是边缘，那么用该卷积核去对图像做全图滤波，即是将图像各个位置的边缘都滤出来。不同的特征靠多个不同的卷积核实现。在卷积层中使用参数共享是用来控制参数的数量。每个滤波器与上一层局部连接，同时每个滤波器的所有局部连接都使用同样的参数，此举会同样大大减少网络的参数。

汇聚

它的作用是逐渐降低数据的空间尺寸，这样的话就能减少网络中参数的数量，使得计算资源耗费变少，也能有效控制过拟合。

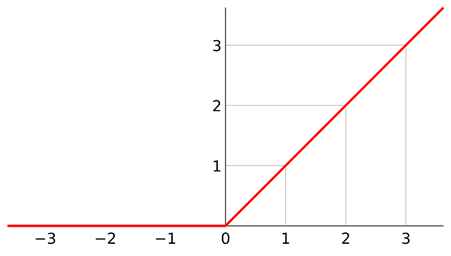
Relu激活函数

Relu，全称为：Rectified Linear Unit，是一种在CNN中常用的激活函数，通常意义下，其指代数学中的斜坡函数，即 f(x)=max(0,x)

优点：

1.x>0 时，梯度恒为1，无梯度耗散问题，收敛快；

2.增大了网络的稀疏性。当x<0 时，该层的输出为0，训练完成后为0的神经元越多，稀疏性越大，提取出来的特征就越具有代表性，泛化(是指训练好的模型在前所未见的数据上的性能好坏)能力越强。即得到同样的效果，真正起作用的神经元越少，网络的泛化性能越好。

3.运算量很小,训练时间少

缺点：

如果后层的某一个梯度特别大，导致W更新以后变得特别大，导致该层的输入<0，输出为0，这时该层就会‘die’，没有更新。当学习率比较大时可能会有40%的神经元都会在训练开始就‘die’，因此需要对学习率进行一个好的设置。

       对于浅层的机器学习，比如经典的三层神经网络，用它作为激活函数的话，那表现出来的性质肯定是线性的。但是在深度学习里，少则几十，多则上千的隐藏层，虽然，单独的隐藏层是线性的，但是很多的隐藏层表现出来的就是非线性的。线性和非线性，举个简单的例子，一条曲线无限分段，每段就趋向直线，反过来，很多这样的直线就可以拟合曲线。类似，大规模的神经网络，包含很多这样的线性基本组件，自然也可以拟合复杂的非线性情况。

 

反向传播

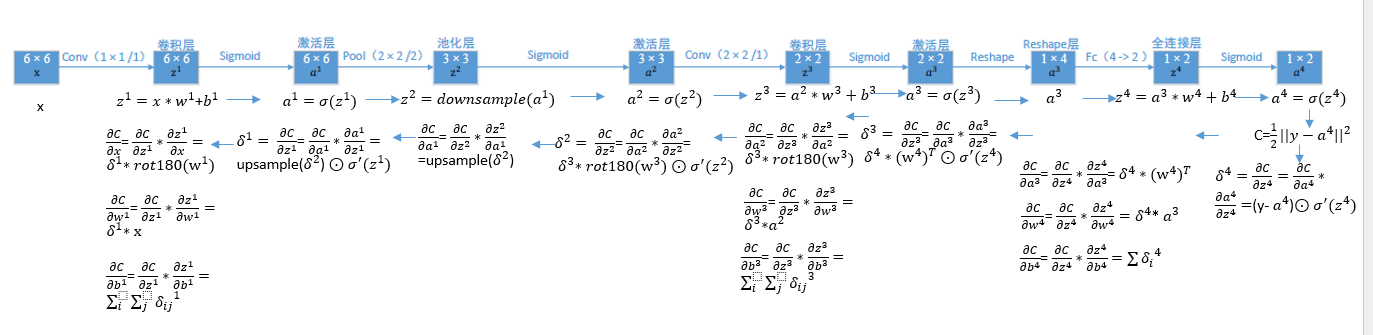
与 BP神经网络一样, CNN 也是通过梯度下降和反向传播算法进行训练的, 则全连接层的梯度公式与 BP网络完全一样, 这里就不重复了. 下面介绍卷积层和池化层的梯度公式.

令输出层的损失为：C=1/2*（y-a^l）²

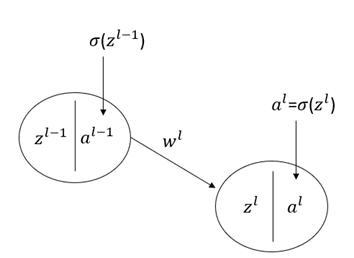
z^l=a^l-1*w^l+b^l

a^l=σ(z^l)

σ表示卷积层神经元的激活函数。a^l-1表示第l层的输入层。

$$\begin{pmatrix} & & \\a_{11}^{l-1}&a_{12}^{l-1}&a_{13}^{l-1} & & \\a_{21}^{l-1}&a_{22}^{l-1}&a_{23}^{l-1} & & \\a_{31}^{l-1}&a_{32}^{l-1}&a_{33}^{l-1} \end{pmatrix} *\begin{pmatrix} & \\w_{11}^{l}&w_{12}^{l} & \\w_{21}^{l}&w_{22}^{l} \end{pmatrix}=*\begin{pmatrix} & \\z_{11}^{l}&_{12}^{l} & \\z_{21}^{l}&z_{22}^{l} \end{pmatrix}$$ 池化层向前一隐藏层的反向传播 在前向传播时，我们一般使用max或average对输入进行池化，而且池化区域已知。反向传播就是要从缩小后的误差δ^(l+1)，还原池化前较大区域对应的误差δ^l. 假设现在我们是步长为1的2×2池化，4×4大小的区域经过池化后变为2*2.如果δ^(l+1)的第k个子矩阵为：$$\delta _{k}^{l+1}=\begin{pmatrix} & \\2&8 & \\4&6 \end{pmatrix}$$ 首先我们要确定$$\delta _{k}^{l+1}中4个误差值分别和原来 4×4大小的哪个子区域所对应，根据前向传播中池化窗口的移动过程，我们可以确定2对应左上角 2×2的区域，8对应右上角 2×2的区域，以此类推。这一步完成之后，我们就要对不同类型的池化进行不同的操作。 如果是 max pooling，我们只需要记录前向传播中最大值的位置，然后将误差放回去即可。如果最大值位置分别为2×2的左上，右下，右上，做下，还原后的矩阵为： \begin{pmatrix} & & & \\2&0&0&0 & & & \\0&0&0&8 & & & \\0&4&0&0 & & & \\0&0&6&0 \end{pmatrix} 如果是average pooling，我们只需要将池化单元的误差平均值放回原来的子矩阵即可： \begin{pmatrix} & & & \\0.5&0.5&2&2 & & & \\0.5&0.5&2&2 & & & \\1&1&1.5&1.5 & & & \\1&1&1.5&1.5 \end{pmatrix} 卷积层向前一隐藏层的反向传播 假设l-1层的激活输出是一个的矩阵，第l层卷积核是一个2*2的矩阵，卷积步长为1。现一个例子来进行理论推导，其中a^(l-1)表示l-1层的输出，z^l表示l层的输入，于是有：

\[z_{11}^{l}=a_{11}^{l-1}*w_{11}^{l}+a_{12}^{l-1}*w_{12}^{l}+a_{21}^{l-1}*w_{21}^{l}+a_{22}^{l-1}*w_{22}^{l} \]

\[z_{12}^{l}=a_{12}^{l-1}*w_{11}^{l}+a_{13}^{l-1}*w_{12}^{l}+a_{22}^{l-1}*w_{21}^{l}+a_{23}^{l-1}*w_{22}^{l} \]

\[z_{21}^{l}=a_{21}^{l-1}*w_{11}^{l}+a_{22}^{l-1}*w_{12}^{l}+a_{31}^{l-1}*w_{21}^{l}+a_{32}^{l-1}*w_{22}^{l} \]

\[z_{22}^{l}=a_{22}^{l-1}*w_{11}^{l}+a_{23}^{l-1}*w_{12}^{l}+a_{32}^{l-1}*w_{21}^{l}+a_{33}^{l-1}*w_{22}^{l} \]

故

\[\delta _{}^{l-1}=\frac{\partial C}{\partial z_{}^{l-1}}=\frac{\partial C}{\partial z_{}^{l}}*\frac{\partial z_{}^{l}}{\partial z_{}^{l-1}}=\delta _{}^{l}*\frac{\partial z_{}^{l}}{\partial a_{}^{l-1}}*\frac{\partial a_{}^{l-1}}{\partial z_{}^{l-1}}=\delta _{}^{l}*\frac{\partial z_{}^{l}}{\partial a_{}^{l-1}}*\sigma’(z_{}^{l-1}) \]

同时

\[\Delta a_{}^{l-1}=\frac{\partial C}{\partial a_{}^{l-1}}=\frac{\partial C}{\partial z_{}^{l}}*\frac{\partial z_{}^{l}}{\partial a_{}^{l-1}}=\delta _{}^{l}*\frac{\partial z_{}^{l}}{\partial a_{}^{l-1}} \]

所以

\[\delta _{}^{l-1}=\Delta a_{}^{l-1}*\sigma’ (z_{}^{l-1}) \]

且

\[\delta a_{11}^{l-1}=\delta _{11}^{l}*w_{11}^{l} \]

\[\delta a_{12}^{l-1}=\delta _{11}^{l}*w_{12}^{l} +\delta _{12}^{l}*w_{11}^{l} \]

\[\delta a_{13}^{l-1}=\delta _{12}^{l}*w_{12}^{l} \]

\[\delta a_{21}^{l-1}=\delta _{11}^{l}*w_{21}^{l} +\delta _{21}^{l}*w_{11}^{l} \]

\[\delta a_{22}^{l-1}=\delta _{11}^{l}*w_{22}^{l} +\delta _{12}^{l}*w_{21}^{l}+\delta _{21}^{l}*w_{12}^{l} +\delta _{22}^{l}*w_{11}^{l} \]

\[\delta a_{23}^{l-1}=\delta _{12}^{l}*w_{22}^{l} +\delta _{22}^{l}*w_{12}^{l} \]

\[\delta a_{31}^{l-1}=\delta _{21}^{l}*w_{21}^{l} \]

\[\delta a_{31}^{l-1}=\delta _{21}^{l}*w_{22}^{l} +\delta _{21}^{l}*w_{21}^{l} \]

\[\delta a_{33}^{l-1}=\delta _{22}^{l}*w_{22}^{l} \]

总结得：

\[\begin{pmatrix} & & & \\0&0&0&0 & & & \\0&\delta _{11}^{l}&\delta _{12}^{l}&0 & & & \\0&\delta _{21}^{l}&\delta _{22}^{l}&0 & & & \\0&0&0&0 \end{pmatrix}* \begin{pmatrix} & \\w_{22}^{l}&w_{21}^{l} & \\w_{12}^{l}&w_{11}^{l} \end{pmatrix}\]

=

\[\begin{pmatrix} & & & \\0&0&0&0 & & & \\0&\delta _{11}^{l}&\delta _{12}^{l}&0 & & & \\0&\delta _{21}^{l}&\delta _{22}^{l}&0 & & & \\0&0&0&0 \end{pmatrix}*rot180\begin{pmatrix} & \\w_{11}^{l}&w_{12}^{l} & \\w_{21}^{l}&w_{22}^{l} \end{pmatrix}\]

=$$\begin{pmatrix}
& & \ \Delta a^{l-1}&\Delta a_{12}^{l-1}&\Delta a_{13}^{l-1}
& & \ \Delta a_{21}^{l-1}&\Delta a_{22}^{l-1}&\Delta a_{23}^{l-1}
& & \ \Delta a_{31}^{l-1}&\Delta a_{32}^{l-1}&\Delta a_{33}^{l-1}
\end{pmatrix}$$
所以得出最终结果：

\[\delta _{}^{l-1}=\Delta a_{}^{l-1}*\sigma‘(z_{}^{l-1})=\delta _{}^{l} *rot180(W_{}^{l})*\sigma‘_{}^{l-1} \]

再对w求偏导：

\[\frac{\partial C}{\partial w_{}^{l}}=\frac{\partial C}{\partial z_{}^{l}}*\frac{\partial z_{}^{l}}{\partial W_{}^{l}}=\delta _{}^{l}*\frac{\partial z_{}^{l}}{\partial W_{}^{l}} \]

\[\Delta w_{11}^{l} =\delta _{11}^{l}*a_{11}^{l-1}+\delta _{12}^{l}*a_{12}^{l-1}+\delta _{21}^{l}*a_{21}^{l-1}+\delta _{22}^{l}*a_{22}^{l-1} \]

\[\Delta w_{12}^{l} =\delta _{11}^{l}*a_{12}^{l-1}+\delta _{12}^{l}*a_{13}^{l-1}+\delta _{21}^{l}*a_{22}^{l-1}+\delta _{22}^{l}*a_{23}^{l-1} \]

\[\Delta w_{21}^{l} =\delta _{11}^{l}*a_{21}^{l-1}+\delta _{12}^{l}*a_{22}^{l-1}+\delta _{21}^{l}*a_{31}^{l-1}+\delta _{22}^{l}*a_{32}^{l-1} \]

\[\Delta w_{22}^{l} =\delta _{11}^{l}*a_{22}^{l-1}+\delta _{12}^{l}*a_{23}^{l-1}+\delta _{21}^{l}*a_{32}^{l-1}+\delta _{22}^{l}*a_{33}^{l-1} \]

整理得：

\[\begin{pmatrix} & & \\a_{11}^{l-1}&a_{12}^{l-1}&a_{13}^{l-1} & & \\a_{21}^{l-1}&a_{22}^{l-1}&a_{23}^{l-1} & & \\a_{31}^{l-1}&a_{32}^{l-1}&a_{33}^{l-1} \end{pmatrix}* \begin{pmatrix} & \\ \delta _{11}^{l}&\delta _{12}^{l}& & \\ \delta _{21}^{l}&\delta _{22}^{l}& \end{pmatrix} = \begin{pmatrix} & \\ \Delta w_{11}^{l}&\Delta w_{12}^{l} & \\ \Delta w_{21}^{l}&\Delta w_{22}^{l} \end{pmatrix}\]

总结得：

\[\frac{\partial C}{\partial W_{}^{l}}=\frac{\partial C}{\partial z_{}^{l}}*\frac{\partial z_{}^{l}}{\partial W_{}^{l}}=\delta _{}^{l}*\frac{\partial z_{}^{l}}{\partial W_{}^{l}}=\delta _{}^{l}*a_{}^{l-1} \]

而对于b, 通常的做法是将误差δ的各个子矩阵的项分别求和，得到一个误差向量，即为b的梯度：

\[\frac{\partial C}{\partial b_{}^{l}}=\frac{\partial C}{\partial a_{}^{l}}*\frac{\partial a_{}^{l}}{\partial z_{}^{l}}*\frac{\partial z_{}^{l}}{\partial b_{}^{l}}=\sum_{}^{}\delta _{}^{l} \]

举个例子：

 

优点 1.共享卷积核，对高维数据处理无压力 2. 无需手动选取特征，训练好权重，即得特征分类效果好 缺点 1.需要调参，需要大样本量，训练最好要GPU 2.物理含义不明确（也就说，我们并不知道没个卷积层到底提取到的是什么特征，而且神经网络本身就是一种难以解释的“黑箱模型”）

参考： [1]由卷积三种模式：full，same，valid到边缘信息处理的思考 https://blog.csdn.net/Mr_Pend/article/details/109439485 [2]卷积神经网络算法实例 https://blog.csdn.net/weixin_30588907/article/details/97870523 [3]卷积神经网络反向传播理论推导 https://blog.csdn.net/Hearthougan/article/details/72910223 [4]深入理解卷积层，全连接层的作用意义 https://blog.csdn.net/m0_37407756/article/details/80904580 [5]【深度学习】卷积神经网络+反向传播推导+爱因斯坦求和约定+numpy_python实现 https://blog.csdn.net/jin739738709/article/details/101829768