【二分查找】4. 寻找两个有序数组的中位数

题目：

 

 

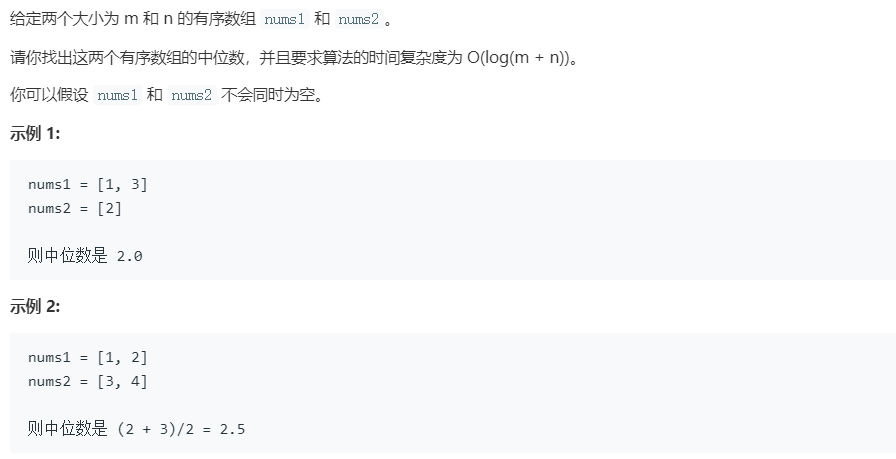
解答：

方法一：

简单粗暴，先将两个数组合并，两个有序数组的合并也是归并排序中的一部分。然后根据奇数，还是偶数，返回中位数。

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) 
    {
        int m = nums1.size();
        int n = nums2.size();
        vector<int> nums;

        int i = 0;
        int j = 0;
        while (i < m && j < n)
        {
            if (nums1[i] < nums2[j])
            {
                nums.push_back(nums1[i++]);
            }
            else if (nums1[i] >= nums2[j])
            {
                nums.push_back(nums2[j++]);
            }
        }

        while (i < m)
        {
            nums.push_back(nums1[i++]);
        }
        while (j < n)
        {
            nums.push_back(nums2[j++]);
        }
        
        if (nums.size() % 2 == 0)
        {
            // std::cout << nums[0] << "\t" << nums[1] << "\t" << nums[2] << "\t" << nums[3];
            return (nums[nums.size() /  2 - 1] + nums[nums.size()/2]) / 2.0;
        }
        else
        {
            // std::cout << nums[0] << "\t" << nums[1] << "\t" << nums[2] << std::endl;
            return nums[nums.size()/2];
        }
    }
};

 

方法二：

 

 

 

 

 

 https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/4-xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-shu/

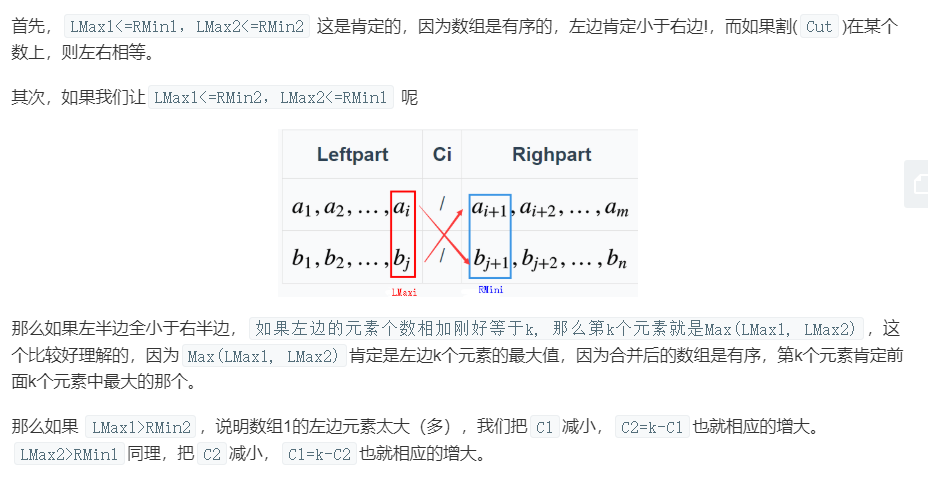
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) 
    {
        int n = nums1.size();
        int m = nums2.size();

        if (n > m)  
        {
            // 保证数组1一定最短
            return findMedianSortedArrays(nums2, nums1);
        }

        // Ci 为第i个数组的割,比如C1为2时表示第1个数组只有2个元素。
        // LMaxi为第i个数组割后的左元素。RMini为第i个数组割后的右元素。
        int LMax1, LMax2, RMin1, RMin2;
        int c1, c2, lo = 0, hi = 2 * n;  //我们目前是虚拟加了'#'所以数组1是2*n长度

        while (lo <= hi)   //二分
        {
            c1 = (lo + hi) / 2;  //c1是二分的结果
            c2 = m + n - c1;

            LMax1 = (c1 == 0) ? INT_MIN : nums1[(c1 - 1) / 2];
            RMin1 = (c1 == 2 * n) ? INT_MAX : nums1[c1 / 2];
            LMax2 = (c2 == 0) ? INT_MIN : nums2[(c2 - 1) / 2];
            RMin2 = (c2 == 2 * m) ? INT_MAX : nums2[c2 / 2];

            if (LMax1 > RMin2)
                hi = c1 - 1;
            else if (LMax2 > RMin1)
                lo = c1 + 1;
            else
                break;
        }
        return (max(LMax1, LMax2) + min(RMin1, RMin2)) / 2.0;        
    }
};