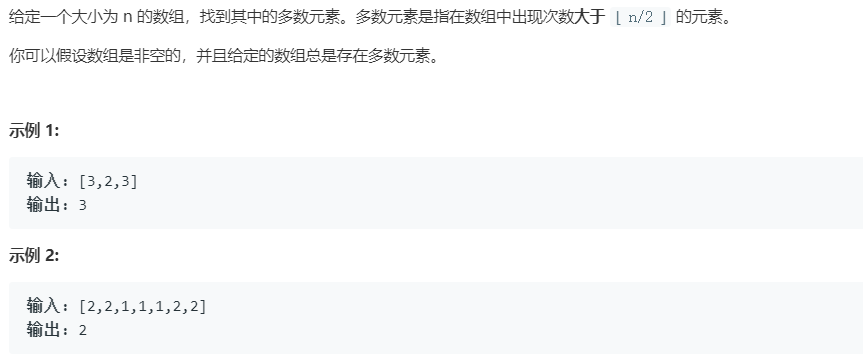
【数组】169. 多数元素-数组中出现次数大于[n/2]的元素

题目：

 

 

解答：

思路：

如果我们把众数记为+1，把其他数记为-1，将它们全部加起来，显然和大于0，从结果本身我们可以看出众数比其他数多。

算法：

Boyer-Moore算法的详细步骤如下：

1）维护一个候选众数candidate和它出现的次数count。初始时，candidate可以为任意值，count为0；

2）遍历数组nums中的所有元素，对于每个元素x，在判断x之前，如果count的值为0，我们先将x的值赋值给candidate，随后我们判断x：

　　A. 如果x与candidate相等，那么计数器count的值增加1；

　　B. 如果x与candidate不等，那么计数器count的值减少1；

3）在遍历完成后，candidate即为整个数组的众数。

 

class Solution {
public:
    int majorityElement(vector<int>& nums) 
    {
        int curNum = nums[0];
        int len = nums.size();

        int count = 1;
        for (int i = 1; i < len; ++i)
        {
            if (count == 0)
            {
                curNum = nums[i]; 
                count = 1;
            }
            else
            {
                if (nums[i] != curNum) 
                {
                    count--;
                }
                else 
                {
                    count++;
                }
            }
        }

        return curNum;
    }
};