【数组】53. 最大和的连续子序列

题目：

 

 

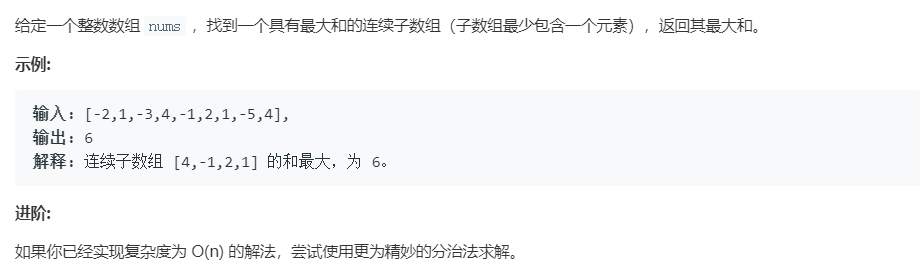
解答：

当我们加上一个正数的时候，和会增加；当我们加上一个负数的时候，和会减少。如果当前得到的和是个负数，那么这个和接下来的累加中应该抛弃并重新清零，不然的话，这个负数将会减少接下来的和。

class Solution {
public:
    int maxSubArray(vector<int>& nums) 
    {
        // int sum = 0;//leetcode通不过
        
        // 其实要处理全是负数的情况，很简单，如稍后下面第三点所见
        // 直接把这句改成："int sum = A[0]"即可
        // 也可以不改，当全是负数的时候，直接返回0，也不见得不行
        int sum = nums[0];
         
        int b = 0;
        for(int i = 0; i < nums.size(); i++)
        {
            if(b < 0)
            {
                b = nums[i];
            }
            else
            {
                b += nums[i];
            }
            if(sum < b)
            {
                sum = b;
            }
        }
        return sum; 
    }
};

 

方法二：动态规划

思路和算法：

假设nums数组的长度是n，下标从0到n-1。

我们用a_i代表nums[i]，用f(i)代表以第i个数结尾的[连续子数组的最大和]，那么很显然我们要求的答案就是：max{f(i)}，其中0<= i <= n -1。

因此，我们只需要求出每个位置的f(i)，然后返回f数组中的最大值即可。那么我们如何求f(i)呢？可以考虑a_i单独成为一段还是加入f(i-1)对应的那一段，这取决于a_i和f(i-1) + a_i的大小，我们希望获得一个比较大的，于是可以写出这样的动态规划转移方程：f(i) = max{f(i-1) + a_i, a_i}

不难给出一个时间复杂度O(n)、空间复杂度O(n)的实现，即用一个f数组来保存f(i)的值，用一个循环求出所有的f(i)。考虑到f(i)只与f(i-1)相关，于是我们可以只用一个变量pre来维护对于当前f(i)的f(i-1)的值是多少，从而让空间复杂度降低到O(1)，这有点类似[滚动数组]的思想。

class Solution {
public:
    int maxSubArray(vector<int>& nums) 
    {
        int pre = 0;
        int maxAns = nums[0];

        for (int i = 0; i < nums.size(); i++) 
        {
            pre = max(pre + nums[i], nums[i]);
            maxAns = max(maxAns, pre);
        }
        return maxAns;        
    }
};