2025寒假集训
1.斜率优化dp
设\(f[i]\)为以\(i\)结尾最大的修正战斗力
易得状态转移方程\(f[i]=max(f[j]+a*(s[i]-s[j])^2+b*(s[i]-s[j])+c)\)
其中\(1 \le j \le i-1\)
把方程化简得:\(f[i]=f[j]+a*s[i]^2-2*a*s[i]*s[j]+a*s[j]^2+b*s[i]-b*s[j]+c\)
将含有\(i\)的项放在一起,含\(j\)的项放在一起
\(f[i]-a*s[i]^2-b*s[i]=-2*a*s[i]*s[j]+a*s[j]^2-b*s[j]+c\)
含\(i\)的项作为一次函数\(y=kx+b\)即\(b=y-kx\)的\(b\)
既含\(i\)又含\(j\)的项作为k,\(k=-2*a*s[i],x=s[j]\)只含\(j\)的项作为\(y=a*s[j]^2-b*s[j]+c\)
那么我们要求\(f[i]\)的最大值,所以要让\(b\)这个整体最大,既需要维护的是上凸包,原因如下:
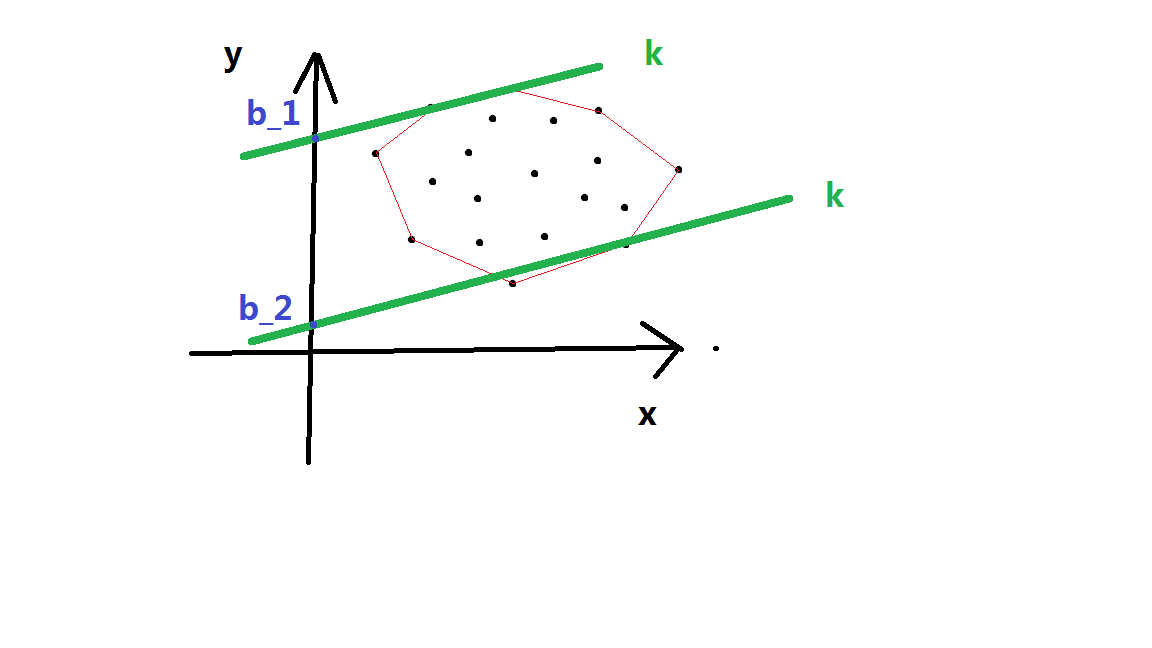
如图显然上凸包上的点的\(b\)值要大于下凸包上的\(b\)值
代码
2.单调队列优化dp
呵呵,以后再补,某人都是用的线段树维护的。。
用线段树维护矩形的长,也就是整个数轴上覆盖次数大于 0 的点。需求列举如下:
(1).一段区间权值加 1、减 1。
(2).统计整个数轴上,区间权值大于 0 的「区间长度和」。
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
const int N=1e5+10;
int n,X[N*2],ans;
struct Line{
int x1,x2,y,mark;
}L[N*2];
struct Tree{
int l,r;
int sum;
int len;
}t[N*16];
bool cmp(Line a,Line b){
return a.y<b.y;
}
void build(int p,int l,int r){
t[p].l=l;t[p].r=r;
t[p].sum=t[p].len=0;
if(l==r){
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
}
void pushup(int p){
if(t[p].sum){
t[p].len=X[t[p].r+1]-X[t[p].l];
}else{
t[p].len=t[p*2].len+t[p*2+1].len;
}
return;
}
void work(int p,int l,int r,int k){
//if(l>t[p].r || r<t[p].l)return;
if(l<=t[p].l && t[p].r<=r){
t[p].sum+=k;
pushup(p);
return;
}
//pushup(p);
int mid=(t[p].l+t[p].r)/2;
if(l<=mid)work(p*2,l,r,k);
if(r>mid)work(p*2+1,l,r,k);
pushup(p);
return;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
L[i]={x1,x2,y1,1};
L[i+n]={x1,x2,y2,-1};
X[i]=x1;
X[i+n]=x2;
}
n*=2;
sort(L+1,L+n+1,cmp);
sort(X+1,X+n+1);
int tot=unique(X+1,X+n+1)-X-1;
build(1,1,tot-1);
for(int i=1;i<n;i++){
int l=lower_bound(X+1,X+tot+1,L[i].x1)-X;
int r=lower_bound(X+1,X+tot+1,L[i].x2)-X;
work(1,l,r-1,L[i].mark);
ans+=(int)(t[1].len*(L[i+1].y-L[i].y));
}
cout<<ans;
return 0;
}
呵呵也是调试了一下午,发现写成lower_bound(X+1,X+n+1,L[i].x1)-X;
4.2-SAT
视频
2-SAT,简单的说就是给出 \(n\) 个集合,每个集合有两个元素,已知若干个 \(\langle a,b \rangle\),表示 \(a\) 与 $b $矛盾(其中 \(a\) 与$ b$ 属于不同的集合)。然后从每个集合选择一个元素,判断能否一共选 \(n\) 个两两不矛盾的元素。显然可能有多种选择方案,一般题中只需要求出一种即可。
解决方法就只会一个tarjan缩点
2-SAT貌似最难的还是建图啊
主要还是判断状态选还是不选
拿例题来说
在模板题中,题目给的要求必须要满足其一,那很好了,直接判断下来,因为是“或”,所以情况比较多,总之就是一个不满足时必须满足另一个,是必须。
在riddle这道题中,虽然正解是拆点建图,但是我们说一下暴力建图的方式,首先要满足1.每一条边连接的两个点必须选择一个2.题目给出的点集内只能有一个被选择:关于1我们很容易得到:不选一个,那么另一个必须选,那么2呢:给出的点一个被选择,其他的必须不选。那为啥不是一个点不选择,然后和其他点选的情况连边?因为不满足必须,一个点不选,其他的点必须都选吗,显然不是;并且有多种情况,不满足“必须”。当然这些是自己抽象出来的一些"策略"吧。
呵呵下面就是优化建图了:当然我也是不会的。
5.网络流
这个也是建图很难,在这个时间节点学会了链式前向星,话说找教程的时候还发现了链式邻接表?附链接
但是自己还是没太弄明白,而且只有在处理反边的时候会用到这个嘞
20240207
模拟赛挂分80,附题目
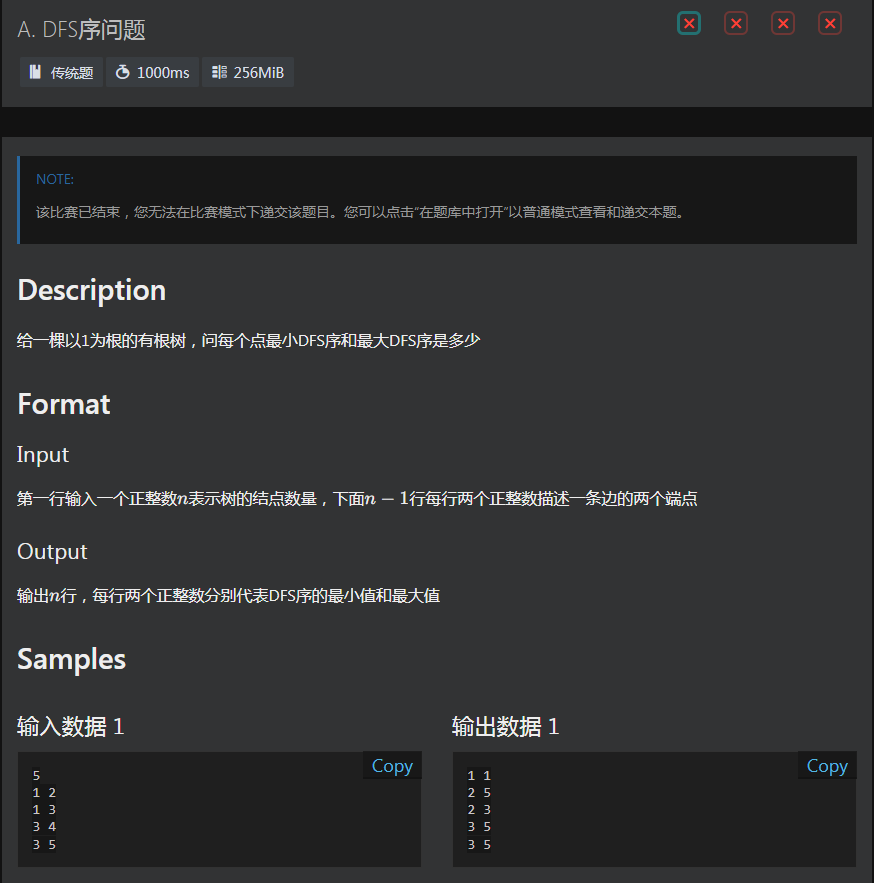
记得建双向边:建单向边1->2 2->1以1为根可能遍历不到2
1.带权并查集
例题1
2.笛卡尔树
这里要给自己代码打上注释 luogu没办法存下来
#include<iostream>
#define int long long
using namespace std;
const int maxn=1e7+1;
int n,ls[maxn],rs[maxn],p[maxn],sta[maxn];
void build()
{
int top=0,cur=0;
for(int i=1;i<=n;i++){
cur=top;
while(cur&&p[sta[cur]]>p[i])//找到第一个比p[i]小的数
cur--;
if(cur)//找到了
rs[sta[cur]]=i;//小根堆,并且(右儿子编号大于根节点编号)
if(cur<top)
ls[i]=sta[cur+1];//把sta[cur+1]作为i的左儿子(要满足左儿子编号小于i的编号)
sta[++cur]=i;
top=cur;
}
return;
}
main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>p[i];
}
build();
int ans1=0,ans2=0;
for(int i=1;i<=n;i++){
ans1^=i*(ls[i]+1);
ans2^=i*(rs[i]+1);
}
cout<<ans1<<' '<<ans2;
return 0;
}
20250208
1.cdq分治(代码待补)
2.贪心
例题
设排序后第 \(i\) 个大臣左右手上的数分别为 \(a_i, b_i\)。考虑通过邻项交换法推导贪心策略。
用 \(s\) 表示第 \(i\) 个大臣前面所有人的 \(a_i\) 的乘积,那么第 \(i\) 个大臣得到的奖赏就是 \(\dfrac{s} {b_i}\),第 \(i + 1\) 个大臣得到的奖赏就是
\(\dfrac{s \cdot a_i} {b_{i+1}}。\)
如果我们交换第$ i$ 个大臣与第 \(i + 1\) 个大臣,那么此时的第 \(i\) 个大臣得到的奖赏就是
\(\dfrac{s} {b_{i+1}}\),第 \(i + 1\) 个大臣得到的奖赏就是
\(\dfrac{s \cdot a_{i+1}} {b_i}\)。
如果交换前更优当且仅当
\(\max \left(\dfrac{s} {b_i}, \dfrac{s \cdot a_i} {b_{i+1}}\right) < \max \left(\dfrac{s} {b_{i+1}}, \dfrac{s \cdot a_{i+1}} {b_i}\right)\)
提取出相同的 s 并约分得到
\(\max \left(\dfrac{1} {b_i}, \dfrac{a_i} {b_{i+1}}\right) < \max \left(\dfrac{1} {b_{i+1}}, \dfrac{a_{i+1}} {b_i}\right)\)
然后分式化成整式得到
\(\max (b_{i+1}, a_i\cdot b_i) < \max (b_i, a_{i+1}\cdot b_{i+1})\)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号