数学

20240806 课件

---

marp: true
math: mathjax

数论入门

整除、同余、数论函数、素数…………………………

by RenaMoe

---

不讲证明的地方是因为用处不大而且俺也不会，请自行了解。

想要严谨而系统的学习 OI 相关的数学知识的话，建议读《具体数学》。

---

基础概念

oi wiki

---

整除

对于正整数 \(n,m\)，如果存在整数 \(q\)，使得 \(n=qm\)，则称 \(m\) 整除 \(n\)，记为 \(m|n\)。

称 \(m\) 是 \(n\) 的约数，\(n\) 是 \(m\) 的倍数。

---

带余除法/取模

对于整数 \(a\) 和正整数 \(b\)，存在整数 \(q,r\) 使得 \(a=qb+r\)，且 \(0\le r< b\)。

\(a\) 对 \(b\) 取模记作 \(a\bmod b=r\) 或者 \(a\equiv r\pmod b\)。

---

最大公约数 gcd

最大的正整数 \(d\) 使得 \(d|a\) 并且 \(d|b\)，则称 \(d\) 是 \(a,b\) 的最大公约数，记作 \(\gcd(a,b)\)（若无歧义有时简记为 \((a,b)\)）。

\(k|a\) 且 \(k|b\) 等价于 \(k|\gcd(a,b)\)。

最小公倍数 \(\mathrm{lcm}(a,b)=\dfrac{ab}{\gcd(a,b)}\)。

拓展到 \(n\) 个数的 \(\gcd,\mathrm{lcm}\)，可以两两合并。

---

求 gcd

辗转相除法，\(\gcd(a,b)=\gcd(b,a\bmod b)\)。

int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

或者 std::__gcd(a, b)。

---

互质

正整数 \(a,b\) 满足 \(\gcd(a,b)=1\)，则称 \(a,b\) 互质，也记作 \(a\perp b\)。

---

取整函数

\(\lfloor x\rfloor\) 表示不大于实数 \(x\) 的最大整数，即 \(\lfloor x\rfloor\le x<\lfloor x\rfloor+1\)。

\(\lceil x\rceil\) 表示不小于实数 \(x\) 的最小整数，即 \(\lceil x\rceil-1<x\le \lceil x\rceil\)。

\(\lfloor\frac{a}{b}\rfloor\)：a / b；

\(\lceil\frac{a}{b}\rceil\)：(a + b - 1) / b。

---

对于整数 \(n\) 和正整数 \(a,b\) 有：

\[\left\lfloor\left\lfloor\frac{n}{a}\right\rfloor/ b\right\rfloor=\left\lfloor\frac{n}{ab}\right\rfloor \]

证：

\(n=qa+r,r\in[0,a-1]\)

\(q=kb+t,t\in[0,b-1]\)

\(n=kab+at+r,at+r\in[0,ab-1]\)

---

整除分块

对于正整数 \(n\)，当 \(1\le d\le n\) 时，\(\left\lfloor\dfrac{n}{d}\right\rfloor\) 的取值个数不超过 \(2\sqrt n\)。

对于 \(\left\lfloor\dfrac{n}{d}\right\rfloor\) 的每一个取值，对应的 \(d\) 是一个区间。

---

整除分块例题

求

\[\sum_{i=1}^n\left\lfloor\dfrac{n}{i}\right\rfloor \]

其中 \(1\le n\le 10^{14}\)。

---

for (long long l = 1, r; l <= n; l = r + 1) {
    r = n / (n / l);
    ans += (r - l + 1) * (n / l);
}

将 \(\left\lfloor\dfrac{n}{i}\right\rfloor\) 相同的一段一块处理，复杂度 \(\mathcal O(\sqrt n)\)。

---

调和数

调和数 \(\displaystyle H_n=\sum_{i=1}^n\frac{1}{i}\)。

\[H_n=\ln n+C+\varepsilon_n \]

\[\sum_{i=1}^n\left\lfloor\frac{n}{i}\right\rfloor=\Theta(n\log n) \]

Luogu P7960 [NOIP2021] 报数

---

素数（质数）

若整数 \(p(p>1)\) 的约数只有 \(1,p\)，则 \(p\) 为质数。

• 简单判断素数算法 \(\mathcal O(\sqrt p)\)，自行了解更快的 Miller Rabin 算法。
• \(1\dots n\) 的质数个数可以估计为 \(\pi(n)\sim\dfrac{n}{\ln n}\)。

---

算数基本定理（唯一分解定理）

任意正整数都可以唯一表示成质数的乘积形式：

\[n=p_1^{c_1}p_2^{c_2}\dots p_k^{c_k} \]

\(p_1,p_2,\dots p_k\) 表示不同的质数。

---

重识 gcd / lcm

唯一分解后，每个正整数都可以看作高维向量 \((c_1,c_2,\dots c_k)\)。

\(\gcd\) 是每一维取 \(\min\)，\(\mathrm{lcm}\) 是每一维取 \(\max\)。

---

分解质因数

正整数 \(n\) 至多有一个 \(> \sqrt n\) 的质因子，暴力做就是 \(\mathcal O(\sqrt n)\)。

vector<int> result;
for (int i = 2; i * i <= N; i++) {
    if (N % i == 0) {
        while (N % i == 0) N /= i;
        result.push_back(i);
    }
}
if (N != 1) {
    result.push_back(N);
}

自行了解更厉害的 Pollard Rho 算法。

---

数论函数 / 积性函数

数论函数指定义域为正整数的函数。

若数论函数 \(f\) 满足当 \(\gcd(a,b)=1\) 时 \(f(ab)=f(a)f(b)\)，则 \(f\) 为积性函数。

若数论函数 \(f\) 满足任何正整数 \(a,b\) 有 \(f(ab)=f(a)f(b)\)，则 \(f\) 为完全积性函数。

---

一些积性函数

• 单位函数 \(\epsilon(n)=[n=1]\)（完全积性）
• 常函数 \(1(n)=1\)（完全积性）
• 恒等函数 \(\mathrm{id}(n)=n\)，\(\mathrm{id}_k(n)=n^k\)（完全积性）
• 除数函数 \(\sigma(n)=\sum_{d|n}d\)，\(\sigma_k(n)=\sum_{d|n}d^k\)
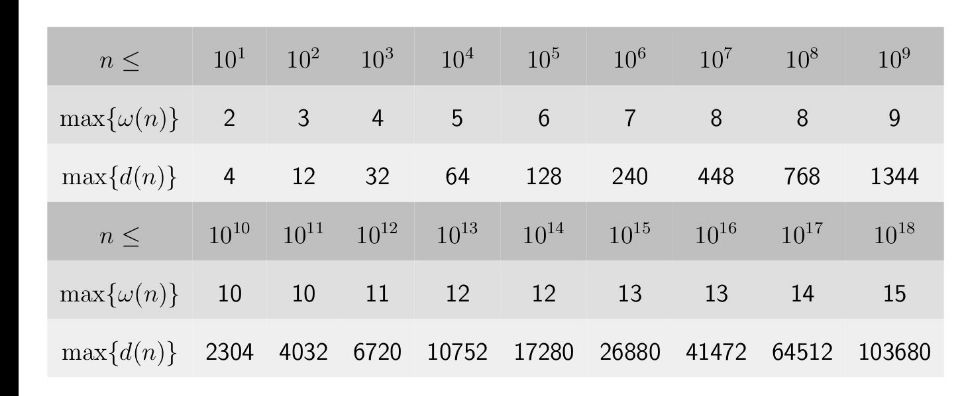
  • \(d(n)=\sigma_0(n)=\sum_{d|n}1\)

---

莫比乌斯函数

\[\mu(n)=\begin{cases}1& n=1\\0& n \text{含有平方因子}\\(-1)^{\omega(n)}&\mathrm{otherwise} \end{cases} \]

\(\omega(n)\) 表示 \(n\) 的本质不同的质因子个数。

---

欧拉函数

欧拉函数 \(\varphi(n)\) 表示小于等于 \(n\) 且与 \(n\) 互质的数的个数。

将 \(n\) 唯一分解 \(n=p_1^{c_1}p_2^{c_2}\dots p_k^{c_k}\)，有

\[\varphi(n)=n\prod_{i=1}^k\left(1-\frac{1}{p_i}\right) \]

---

性质：

• 与 \(n\) 互质的数成对出现，因为 \(\gcd(n,x)=\gcd(n,n-x)=1\)；
• \(n>2\) 时，\(\varphi(n)\) 为偶数；
• \(n>1\) 时，与 \(n\) 互质的数的和为 \(\varphi(n)\cdot\frac{n}{2}\)；
• \(\varphi(p^k)=p^k-p^{k-1}\)（\(p\) 为质数）；
• \(\displaystyle \sum_{d|n}\varphi(d)=n\)；

---

约数个数前缀和

求

\[\sum_{i=1}^n\sigma_0(i) \]

\(n\le 10^{12}\)。

---

考虑每个数的贡献，

\[\begin{aligned} \sum_{i=1}^n\sigma_0(i)&=\sum_{i=1}^n\sum_{d|i}1\\ &=\sum_{d=1}^n\left\lfloor\frac{n}{d}\right\rfloor \end{aligned} \]

整除分块即可，\(\mathcal O(\sqrt n)\)。

更一般地，

\[\sum_{i=1}^n\sigma_k(i)=\sum_{i=1}^ni^k\left\lfloor\frac{n}{i}\right\rfloor \]

---

积性函数的性质

若 \(f(x)\) 和 \(g(x)\) 均为积性函数，则以下函数也为积性函数：

\[\begin{aligned} h(x)&=f(x^p)\\ h(x)&=f^p(x)\\ h(x)&=f(x)g(x)\\ h(x)&=\sum_{d\mid x}f(d)g\left(\dfrac{x}{d}\right) \end{aligned} \]

---

若 \(f\) 是积性函数，\(n=p_1^{c_1}p_2^{c_2}\dots p_k^{c_k}\)，那么

\[f(n)=f(p_1^{c_1})f(p_2^{c_2})\dots f(p_k^{c_k}) \]

研究积性函数 \(f\) 转化为研究 \(f\) 在质数和质数的幂处的取值 \(f(p^k)\)。

---

欧拉筛

线性处理质数或积性函数。

---

朴素想法是从小到大遍历，把每个质数的倍数标记为合数，未被标记的就是下一个质数。

可以了解一下 \(\mathcal O(n\log\log n)\) 的埃氏筛。

欧拉筛要求每个数只在其最小质因子处被筛掉，因此 \(\mathcal O(n)\)。

---

vector<int> pri;
bool not_prime[N];

void pre(int n) {
    for (int i = 2; i <= n; ++i) {
        if (!not_prime[i]) {
            pri.push_back(i);
        }
        for (int pri_j : pri) {
            if (i * pri_j > n) break;
            // pri_j 是 i * pri_j 的最小质因子
            not_prime[i * pri_j] = true;
            if (i % pri_j == 0) {
                break;
            }
        }
    }
}

---

线性筛欧拉函数

讨论质因子 pri_j 是否是第一次出现。

vector<int> pri;
bool not_prime[N];
int phi[N];

void pre(int n) {
  phi[1] = 1;
  for (int i = 2; i <= n; i++) {
    if (!not_prime[i]) {
      pri.push_back(i);
      phi[i] = i - 1;
    }
    for (int pri_j : pri) {
      if (i * pri_j > n) break;
      not_prime[i * pri_j] = true;
      if (i % pri_j == 0) {
        phi[i * pri_j] = phi[i] * pri_j;
        break;
      }
      phi[i * pri_j] = phi[i] * phi[pri_j];
    }
  }
}

---

线性筛 \(\mu,\sigma\) 等积性函数同理，见 oi wiki 的实现

欧拉筛时每次枚举 pri_j 是在加入一个最小质因子，或者使当前最小质因子次数 \(+1\)。

此时可以根据积性函数质因子之间相对独立的性质递推函数值。

对于一般的积性函数，讨论：

• \(f(p)\) 是什么（\(p\) 是质因子）；
• 由 \(f(p^k)\) 推导 \(f(p^{k+1})\)。

---

Dirichlet 卷积

设 \(f,g\) 是数论函数，若数论函数 \(h\) 满足

\[h(n)=\sum_{d|n}f(d)g(\frac{n}{d}) \]

称 \(h\) 是 \(f,g\) 的 Dirichlet 卷积，记作 \(h=f*g\)。

单位函数 \(\epsilon\) 是 Dirichlet 卷积的单位元，\(\epsilon*f=f*\epsilon=f\)。

Dirichlet 卷积满足交换律和结合律。

---

计算 Dirichlet 卷积时从 \(1\) 到 \(n\) 枚举每个数的倍数，\(\mathcal O(n\log n)\)。

for (int i = 1; i <= n; ++i) {
    for (int j = 1; i * j <= n; ++j) {
        h[i * j] += f[i] * g[j];
    }
}

---

Luogu P2303 [SDOI2012] Longge 的问题

link

求

\[\sum_{i=1}^n\gcd(i,n) \]

\(1\le n\le 2^{32}\)。

---

\[\begin{aligned} \sum_{i=1}^n\gcd(i,n)&=\sum_{d|n}d\sum_{i=1}^n{[\gcd(i,n)=d]}\\ &=\sum_{d|n}d\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}{[\gcd(di,n)=d]}\\ &=\sum_{d|n}d\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}{[\gcd\left(i,\frac{n}{d}\right)=1]}\\ &=\sum_{d|n}d\varphi\left(\frac{n}{d}\right)\\ \end{aligned} \]

暴力做。

---

---

Dirichlet 前缀和

设 \(a=\prod_ip_i^{\alpha_i},b=\prod_ip_i^{\beta_i}\)，那么 \(a\) 贡献到 \(b\) 当前仅当 \(\bigwedge_i[\alpha_i\le \beta_i]\)。

也就是高维前缀和。复杂度与埃氏筛一样 \(\mathcal O(n\log\log n)\)。

for (int p : pri)
    for (int i = 1; i * p <= n; ++i)
        f[i * p] += f[i];

P5495 【模板】Dirichlet 前缀和

---

一些积性函数卷积关系

• \(\mu*1=\epsilon\)
• \(\varphi *1=\mathrm{id}\)
• \(1*1=d\)
• \(\mathrm{id}*1=\sigma\)
• \(\mathrm{id}^k*1=\sigma_k\)

利用 Dirichlet 卷积替换求和式中的一部分，然后交换求和顺序，降低求和的时间复杂度。

---

Mobius 函数的性质

\[\sum_{d|n}\mu(d)=\epsilon(n) \]

即

\[\mu * 1=\epsilon \]

---

*证明：

\(n=1\) 时 \(\mu(1)=1\)。

\(n>1\) 时设 \(n\) 唯一分解后有 \(k\) 个质因子。

当约数含有平方因子时函数值为 \(0\)，因此质因子的次数只有 \(0\) 或 \(1\)。枚举含有 \(i\) 个质因子，

\[\sum_{i=0}^k\binom{k}{i}(-1)^i=(1-1)^k=0 \]

---

欧拉函数的性质

\[\sum_{d|n}\varphi(d)=n \]

即

\[\varphi * 1=\mathrm{Id} \]

---

*证明：

对于 \(i,1\le i\le n\)，设 \(g=\gcd(i,n)\)，那么 \(\gcd(\frac{i}{g},\frac{n}{g})=1\)。

枚举这个最大公约数 \(g\)，\(1\dots \frac{n}{g}\) 中与 \(\frac{n}{g}\) 互质的数有 \(\varphi(\frac{n}{g})\) 个，即对应的 \(i\) 有 \(\varphi(\frac{n}{g})\) 个。

\[n=\sum_{d|n}\varphi\left(\frac{n}{d}\right)=\sum_{d|n}\varphi(d) \]

---

莫比乌斯变换

若数论函数 \(f,g\) 满足

\[g(n)=\sum_{d|n}f(d) \]

即

\[g=f*1 \]

两边同时卷积 \(\mu\) 得到

\[g*\mu=f*\epsilon=f \]

即

\[f(n)=\sum_{d|n}g(d)\mu(\frac{n}{d}) \]

---

典题

求

\[\sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)=1] \]

\(1\le n,m\le 10^7\)。

---

利用 \(\mu *1=\epsilon\)，

\[\begin{aligned} \sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)=1]&=\sum_{i=1}^n\sum_{j=1}^m\sum_{k|\gcd(i,j)}\mu(k)\\ &=\sum_{i=1}^n\sum_{j=1}^m\sum_{k|i,k|j}\mu(k)\\ &=\sum_{k=1}^{\min(n,m)}\mu(k)\left\lfloor\frac{n}{k}\right\rfloor\left\lfloor\frac{m}{k}\right\rfloor \end{aligned} \]

线性筛 \(\mu\) 即可。

---

Luogu P1447 [NOI2010] 能量采集

link

转化后题意：求

\[\sum_{i=1}^n\sum_{j=1}^m2(\gcd(i,j)-1)+1 \]

\(1\le n,m\le 10^5\)。

---

利用 \(\varphi *1=\mathrm{Id}\)，

\[\begin{aligned} &\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)\\ &=\sum_{i=1}^n\sum_{j=1}^m\sum_{d|\gcd(i,j)}\varphi(d)\\ &=\sum_{d=1}^{\min(n,m)}\varphi(d)\left\lfloor\frac{n}{d}\right\rfloor\left\lfloor\frac{m}{d}\right\rfloor\\ \end{aligned} \]

---

LOJ#2000. 「SDOI2017」数字表格

link

设 \(f_i\) 表示斐波那契数列第 \(i\) 项，\(q\) 次查询 \(n,m\) 求

\[\prod_{i=1}^n\prod_{j=1}^mf_{\gcd(i,j)} \]

\(1\le n,m\le 10^6\)，\(1\le q\le 1000\)。

---

利用 \(\mu *1=\epsilon\)，不妨设 \(n,m\)，

\[\begin{aligned} &\prod_{i=1}^n\prod_{j=1}^mf_{\gcd(i,j)}\\ &=\prod_{d=1}^nf_d^{\sum_{i=1}^{\lfloor n/d\rfloor}\sum_{j=1}^{\lfloor m/d\rfloor}[\gcd(i,j)=1]}\\ &=\prod_{d=1}^nf_d^{\sum_{k=1}^{\lfloor n/d\rfloor}\mu(k)\left\lfloor\frac{n}{dk}\right\rfloor\left\lfloor\frac{m}{dk}\right\rfloor}\\ &=\prod_{T=1}^n\left(\prod_{d|T} f_d^{\mu(\frac{T}{d})}\right)^{\left\lfloor\frac{n}{T}\right\rfloor\left\lfloor\frac{m}{T}\right\rfloor}\\ \end{aligned} \]

整除分块，\(\mathcal O(T\sqrt n\log\cdot)\)。submission

---

模运算性质

• \(a\equiv b\pmod p,b\equiv c\pmod p\Longrightarrow a\equiv c\pmod p\)
• 若 \(a\equiv n\pmod p,b\equiv m\pmod p\)，则：
  • \(a+b\equiv n+m\pmod p\)
  • \(a-b\equiv n-m\pmod p\)
  • \(a\times b\equiv n\times m\pmod p\)

---

剩余系

“剩余系”就是指对于某一个特定的正整数 \(p\)，一个整数集中的数模 \(p\) 所得的余数域。

如果一个剩余系中包含了这个正整数所有可能的余数（一般地，对于任意正整数 \(p\)，有 \(p\) 个余数：\(0,1,2,...,p-1\)），那么就被称为是模 \(p\) 的一个完全剩余系。

将对整数的所有运算限制在剩余系中进行(每次运算完后取模)，各种性质都将得以保持。

---

若 \(a,p\) 互质，那么 \(ak\)（\(0\le k< p\)）会遍历整个 \(\bmod p\) 的剩余系。

若 \(\gcd(a,p)=d\)，那么 \(ak\) 只能遍历 \(\bmod p\) 的剩余系中 \(d\) 的倍数。

---

裴蜀定理

设 \(a,b\) 是不全为零的整数，对任意整数 \(x,y\) ，满足 \(\gcd(a,b)\mid ax+by\)；

且存在整数 \(x,y\) , 使得 \(ax+by=\gcd(a,b)\)。

---

扩展欧几里得算法

用于求解 \(ax+by=\gcd(a,b)\) 的一组可行解。

\[ax_1+by_1=\gcd(a,b) \]

\[bx_2+(a\bmod b)y_2=\gcd(b,a\bmod b) \]

又 \(\gcd(a,b)=\gcd(b,a\bmod b)\)，

\[\begin{aligned} ax_1+by_1&=bx_2+(a\bmod b)y_2\\ &=bx_2+(a-\lfloor\tfrac{a}{b}\rfloor b)y_2\\ &=ay_2+b(x_2-\lfloor\tfrac{a}{b}\rfloor y_2)\\ \end{aligned} \]

---

\[ax_1+by_1=ay_2+b(x_2-\lfloor\tfrac{a}{b}\rfloor y_2) \]

int exgcd(int a, int b, int &x, int &y) {
    if (!b) {
        x = 1;
        y = 0;
        return a;
    }
    int g = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return g;
}

---

线性同余方程

模板题

求解

\[ax\equiv c\pmod b \]

等价于二元一次不定方程 \(ax+by=c\) 。

---

方程有解的充要条件是 \(\gcd(a,b)\mid c\) 。

通过 exgcd 可以求出 \(ax+by=\gcd(a,b)\) 的一组解 \(x_0,y_0\)，

\[ax_0+by_0=\gcd(a,b) \]

\[a\frac{cx_0}{\gcd(a,b)}+b\frac{cy_0}{\gcd(a,b)}=c \]

---

此时得到 \(ax+by=c\) 的一组解 \(x_0,y_0\)，构造

\[a\left(x_0+t\frac{b}{\gcd(a,b)}\right)+b\left(y_0-t\frac{a}{\gcd(a,b)}\right)=c \]

其中 \(t\) 为任意整数。得到方程任意解的表示。

---

费马小定理

若 \(p\) 为质数，则

\[a^{p-1}\equiv 1\pmod p \]

---

欧拉定理

若 \(\gcd(a,m)=1\)，则

\[a^{\varphi(m)}\equiv 1\pmod m \]

---

扩展欧拉定理

当 \(\gcd(a,m)= 1\) 时，

\[a^b\equiv a^{b \bmod \varphi(m)}\pmod m \]

当 \(\gcd(a,m)\ne 1\) 时，

\[a^b \equiv \begin{cases} a^b, &b < \varphi(m), \\ a^{(b \bmod \varphi(m)) + \varphi(m)}, &b \ge \varphi(m). \end{cases} \pmod m \]

这是因为模 \(m\) 意义下 \(a^b\) 是一个 \(\rho\) 形环，环长为 \(\varphi(m)\)。

---

乘法逆元

若 \(ab\equiv 1\pmod m\)，称 \(b\) 是 \(\bmod m\) 意义下 \(a\) 的乘法逆元，记作 \(a^{-1}\)。

• 若 \(m\) 为质数，根据费马小定理，快速幂计算 \(a^{m-2}\pmod m\)；
• 若 \(\gcd(a,m)=1\)，根据欧拉定理，转化为 \(ax+my=1\) 用 exgcd 求解 \(x\)。

---

*线性求逆元

将 \(i^{-1}\) 从 \((p\bmod i)^{-1}\) 转移过来。

令 \(k=\lfloor\frac{p}{i}\rfloor,j=p\bmod i\)，有 \(p=ki+j\)，

\[\begin{aligned} ki+j&\equiv 0\pmod p\\ kj^{-1}+i^{-1}&\equiv 0\pmod p\\ i^{-1}&\equiv -kj^{-1}\pmod p\\ i^{-1}&\equiv -\left\lfloor\frac{p}{i}\right\rfloor(p\bmod i)^{-1}\pmod p\\ \end{aligned} \]

inv[1] = 1;
for (int i = 2; i <= n; ++i) {
    inv[i] = 1ll * (p - p / i) * inv[p % i] % p;
}

---

中国剩余定理

模板题

如下形式的一元线性同余方程组（其中 \(n_1, n_2, \cdots, n_k\) 两两互质）：

\[\begin{cases} x &\equiv a_1 \pmod {n_1} \\ x &\equiv a_2 \pmod {n_2} \\ &\vdots \\ x &\equiv a_k \pmod {n_k} \\ \end{cases} \]

求 \(x\) 最小非负整数解。

---

\[M=\prod_{i=1}^nm_i \]

\[M_i=\frac{M}{m_i} \]

\[t_i\equiv M_i^{-1}\pmod{m_i} \]

\[x\equiv \sum_{i=1}^n{a_it_iM_i}\pmod M \]

为使得 \(x\) 最小，exgcd 求解 \(M_i^{-1}\) 时使 \(t_i\) 尽量小。

---

扩展中国剩余定理

如下形式的一元线性同余方程组（其中 \(b_1, b_2, \cdots, b_k\) 不一定互质）：

\[\begin{cases} x &\equiv a_1 \pmod {b_1} \\ x &\equiv a_2 \pmod {b_2} \\ &\vdots \\ x &\equiv a_k \pmod {b_k} \\ \end{cases} \]

求 \(x\) 最小非负整数解。

---

将方程两两合并，

\[\begin{cases} x &\equiv a_1 \pmod {b_1} \\ x &\equiv a_2 \pmod {b_2} \\ \end{cases} \]

\[\begin{cases} x &= a_1+b_1y_1\\ x &= a_2+b_2y_2\\ \end{cases} \]

\[a_1+b_1y_1=a_2+b_2y_2 \]

\[b_1y_1-b_2y_2=a_2-a_1 \]

当 \(\gcd(b_1,b_2)\nmid (a_2-a_1)\) 时无解。

当 \(\gcd(b_1,b_2)\mid (a_2-a_1)\) 时转化为线性同余方程问题。

---

exgcd 可以解得 \(b_1y_1+b_2(-y_2)=a_2-a_1\) 中 \(y_1\) 一个解记为 \(Y_0=y_0\dfrac{a_2-a_1}{\gcd(b_1,b_2)}\)。

通解

\[y_1=Y_0+t\frac{b_2}{\gcd(b_1,b_2)} \]

\(x=a_1+b_1y_1\)，令 \(y_1\) 最小使得 \(x\) 最小。

合并后方程

\[x\equiv b_1y_1+a_1\pmod {\mathrm{lcm}(b_1,b_2)} \]

---

Lucas 定理内容

对于质数 \(p\)，有

\[\binom{n}{m}\bmod p = \binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}\cdot\binom{n\bmod p}{m\bmod p}\bmod p \]

只需预处理 \(\mathcal O(p)\) 的组合数，递归做。

---

*二次剩余

---

阶

\(a\) 在模 \(p\) 意义下的阶为，最小的整数 \(k\)，满足 \(a^k\equiv 1\pmod p\)。

记为 \(\delta_p(a)\)。

由欧拉定理可知 \(\delta_p(a)\mid \varphi(p)\)。

---

原根

满足 \(g\) 在模 \(p\) 意义下的阶等于 \(\varphi(p)\)，即 \(\delta_p(g)=\varphi(p)\) 的 \(g\)。

注：\(2,4,p^c,2p^c\)（\(p\) 为奇质数）才有原根。

当 \(p\) 是质数时，\(g^0,g^1\dots g^{\varphi(p)-1}\) 遍历除 \(0\) 以外整个 \(\bmod p\) 剩余系。

---

*求原根

先求最小原根。已被证明的结论：\(p\) 最小原根的范围不超过 \(p^{0.25}\)。

大力枚举 \(g\)，然后判定：对于 \(1\le j<\varphi(p)\)，\(g^j\not\equiv 1\pmod p\)。

阶的性质：如果 \(\gcd(a,p)=1\)，且 \(a^k\equiv 1\pmod p\)，那么 \(k|\varphi(p)\)。

只需要枚举 \(\varphi(p)\) 的所有质因子 \(c_i\)，判定 \(\displaystyle g^{\frac{\varphi(p)}{c_i}}\not\equiv 1\pmod p\)，能够覆盖所有 \(\varphi(p)\) 真因子的倍数。

所有原根可以通过最小原根 \(g\) 构造出来，即所有的 \(g^k\)，其中 \(k\in[1,\varphi(p)]\) 且 \(\gcd(k,\varphi(p))=1\)。

code

---

离散对数

求解

\[a^x\equiv b\pmod m \]

其中 \(a,m\) 互质。

---

大步小步算法（BSGS）

设 \(t=\lceil\sqrt m\rceil\)，把 \(x\) 拆成 \(i\cdot t-j\) 的形式。

\[\begin{aligned} a^{i\cdot t-j}&\equiv b\pmod m\\ a^{i\cdot t}&\equiv b\cdot a^{j}\pmod m \end{aligned} \]

枚举 \(j\) 将 \(b\cdot a^{j}\) 插入哈希表，再枚举 \(i\) 查询 \(a^{i\cdot t}\)。

复杂度 \(\mathcal O(\sqrt p)\)。

---

i64 BSGS(int a, int b, int p) {
    map<i64, i64> m;
    b %= p;
    if (a % p == 0) {// 特判
        if (b == 0) return 1;
        else return -1;
    }
    i64 t = ceil(sqrt(p));
    for (i64 i = 0, bn = b; i <= t; ++i) {
        m[bn] = i;
        bn = bn * a % p;
    }
    a = power(a, t);
    for (i64 i = 0, an = 1, j; i <= t; ++i) {
        if (m.count(an)) {
            j = m[an];
            if (i * t - j >= 0) return i * t - j;
        }
        an = an * a % p;
    }
    return -1;
}

---

扩展 BSGS

若 \(a,p\) 不互质，设 \(d=\gcd(a,p)\)，

\[\begin{aligned} a^{x-1}\times a&\equiv b &\pmod p\\ a^{x-1}\times \frac{a}{d}&\equiv \frac{b}{d} &\pmod{\frac{p}{d}}\\ a^{x-1}&\equiv \frac{\frac{b}{d}}{\frac{a}{d}}&\pmod{\frac{p}{d}} \end{aligned} \]

递归处理直到 \(a,p\) 互质，此时可以进行 BSGS 算法。

---

模板题

i64 exBSGS(i64 a, i64 b, i64 p) {
    a %= p, b %= p;
    if (b == 1 || p == 1) return 0; // 特判
    i64 d, cnt = 0, ad = 1; // 分别是gcd(a,p)，循环次数，a/d
    while ((d = gcd(a, p)) > 1) {
        if (b % d) return -1;
        cnt++, b /= d, p /= d, ad = ad * a / d % p;
        if (ad == b) return cnt;
    }
    i64 ans = BSGS(a, b, p, ad);
    return ans == -1 ? -1 : ans + cnt;
}

---

\[\prod_{i=1}^na_i\equiv \prod_{i=1}^ng^{c_i}\equiv g^{\sum_{i=1}^nc_i}\pmod p \]

离散对数可以将 \(\bmod p\) 的乘法转化为 \(\bmod \varphi(p)\) 的加法。

---

离散对数变形

求解

\[x^a\equiv b\pmod p \]

其中 \(p\) 为质数。

---

找到 \(p\) 的原根，\(x\) 就一定可以表示为 \(x\equiv g^c\pmod p\)。

\[\left(g^c\right)^a\equiv b\pmod p \]

\[g^{ac}\equiv b\pmod p \]

转化为求解 \(ac\)。

---

谢谢大家。