AtCoder Beginner Contest 375
A - Seats
思路
枚举即可
AC代码
#include<bits/stdc++.h>
#define endl '\n'
#define int int long long
#define pb push_back
#define bs bitset
using namespace std;
typedef pair<char,int> PCI;
typedef pair<int,int> PII;
typedef priority_queue<int> PQ;
const int N = 2e5+10, MAX = 1e9, INF = -1e9;
int n;
string s;
int ans=0;
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n;
cin>>s;
s=" "+s;
for(int i=1;i<=n-2;i++){
if(s[i]=='#'&&s[i+1]=='.'&&s[i+2]=='#')ans++;
}
cout<<ans<<endl;
return 0;
}
B - Traveling Takahashi Problem
思路
按照题意模拟即可,注意从开始从原点出发,最后还要回到原点
AC代码
#include<bits/stdc++.h>
#define endl '\n'
#define int int long long
#define pb push_back
#define bs bitset
using namespace std;
typedef pair<char,int> PCI;
typedef pair<int,int> PII;
typedef priority_queue<int> PQ;
const int N = 2e5+10, MAX = 1e9, INF = -1e9;
int n;
double x[N];
double y[N];
double ans=0;
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n;
x[0]=0.0;y[0]=0.0;y[n+1]=0.0;x[n+1]=0.0;
for(int i=1;i<=n;i++){
cin>>x[i]>>y[i];
}
for(int i=0;i<=n;i++){
ans+=sqrt((x[i]-x[i+1])*(x[i]-x[i+1])+(y[i]-y[i+1])*(y[i]-y[i+1]));
}
printf("%.12lf",ans);
return 0;
}
C - Spiral Rotation
思路
读题费了我很长时间,最后10min啃样例才顿悟开始做题,debug最后超赛时8minAC了,遗憾至极,其实C的题目就是提示,(我没有做题看题目的习惯,以后还是要看看), 我们来看看这个过程,整个过程可以看成两个步骤:首先将 \((x, y)\) 变换成 \((N+1-x, y)\) ,这一步就是把原先的点按照 \(x\) 的中轴对称过去,然后第二步将 \((N+1-x, y)\) 变换成 \((y, N + 1 - x)\) ,就是交换 \(x\) 和 \(y\) ,在数学上就是按照从左上到右下的对角线对称过去(参考中学反函数图像的形成);
如下图,\(A\) 点先按照水平绿线对称到 \(A'\) 点,再按照斜的对称线对称到 \(A''\) 点,整体就是按照中心 \(O\) 顺时针旋转了90度:
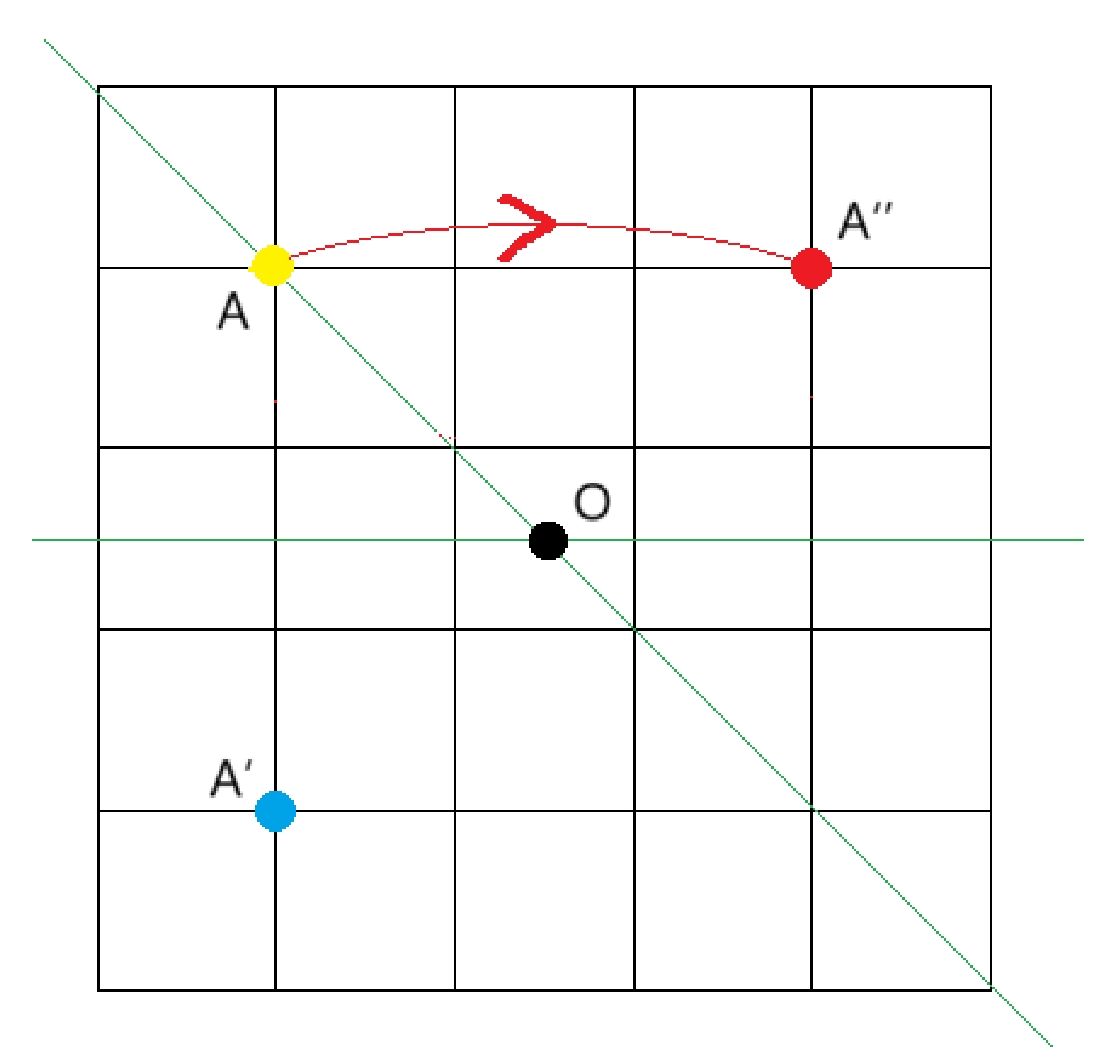
再读题意结合样例不难发现,最外层只参与一次旋转,向内第二次层会转两次,以此类推,所以设由外向内层数为 \(key\) ,则第 \(key\) 层最终就旋转了 \(key\) \(mod4\) 次,考虑类似于冒泡排序的交换方式,编写旋转函数即可;
AC代码
#include<bits/stdc++.h>
#define endl '\n'
#define int int long long
#define pb push_back
#define bs bitset
using namespace std;
typedef pair<char,int> PCI;
typedef pair<int,int> PII;
typedef priority_queue<int> PQ;
const int N = 3005, MAX = 1e9, INF = -1e9;
int n;
char g[N][N];
void f(int key,int m){
int a=m;int b=n+1-m;
while(key--){
for(int i=a;i<b;i++){
char c=g[a][i];
swap(c,g[i][b]);
swap(c,g[b][a+b-i]);
swap(c,g[a+b-i][a]);
swap(c,g[a][i]);
}
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>g[i][j];
}
}
for(int i=1;i<=n/2;i++){
f(i%4,i);
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<g[i][j];
}
cout<<endl;
}
return 0;
}
D - ABA
思路
要达成长度为3的回文串,就需要左右两边相同的字符夹中间任意字符,用map储存每种字符的索引数组,结合样例不难发现对于每个索引,答案就是其后的索引与其作差减一再求和,即:$$\sum_{i=1}^{l-1 }\sum_{j=i+1}^la[j]-a[i]-1$$,时间复杂度为 \(O(n^2)\) ( \(l\) 是每个字符索引数组长度) ,简化公式,用前缀和简化得:$$\sum_{i=0}^l s[l-1]-s[i]-(l-1-i)(a[i]+1)$$,至此我们就在线性时间解决这个问题了;
AC代码
#include<bits/stdc++.h>
#define endl '\n'
#define int int long long
#define pb push_back
#define bs bitset
using namespace std;
typedef pair<char,int> PCI;
typedef pair<int,int> PII;
typedef priority_queue<int> PQ;
const int N = 2e5+10, MAX = 1e9, INF = -1e9;
string s;
map<char ,vector<int>> mp;
int ans=0;
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin>>s;s=" "+s;
int n=s.size();
for(int i=1;i<=n;i++){
mp[s[i]].pb(i);
}
for(auto i:mp){
int l=i.second.size();
int res=0;
int s[l];
for(int j=0;j<l;j++){
res+=i.second[j];
s[j]=res;
}
for(int j=0;j<l;j++){
ans+=(s[l-1]-s[j]-(l-1-j)*(i.second[j]+1));
}
}
cout<<ans<<endl;
}
E - 3 Team Division
思路
\(N\)数量级较小,时间限制有4秒,应该想出一个多项式级别时间复杂度的算法,考虑动态规划:设 \(dp[i][j][k]\) 储存的是前 \(i\) 个成员安排好后,第一组强度为 \(j\) ,第二组强度为 \(k\) 的最小操作数,由于 \(j\) , \(k\)
已知,故第三组的强度也已知,为方便,用pre数组预处理出前 \(i\) 个的强度和,转移方程如下:
\(bool\) 为转移操作是否实行,时间复杂度为三次方,足够解决这个问题了;(注意特判,如果强度和不是3的倍数,那就一定不可能;还可以用滚动数组压缩空间);
AC代码
#include<bits/stdc++.h>
#define endl '\n'
#define int int long long
#define pb push_back
#define bs bitset
using namespace std;
typedef pair<char,int> PCI;
typedef pair<int,int> PII;
typedef priority_queue<int> PQ;
const int N = 1e2 + 5, M = 5e2 + 5;
const int inf = 0x3f3f3f3f3f3f3f3f;
int n;
int a[N], b[N], dp[N][M][M];
void solve()
{
cin >> n;
int sum = 0;
for (int i = 1; i <= n; i++)
{
cin >> a[i] >> b[i];
sum += b[i];
}
if (sum % 3 != 0)
{
cout << -1 << endl;
return;
}
memset(dp, inf, sizeof dp);
dp[0][0][0] = 0, sum /= 3;
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= sum; j++)
{
for (int k = 0; k <= sum; k++)
{
if (dp[i][j][k] == inf)
continue;
if (j + b[i + 1] <= sum)
dp[i + 1][j + b[i + 1]][k] = min(dp[i + 1][j + b[i + 1]][k], dp[i][j][k] + (a[i + 1] != 1));
if (k + b[i + 1] <= sum)
dp[i + 1][j][k + b[i + 1]] = min(dp[i + 1][j][k + b[i + 1]], dp[i][j][k] + (a[i + 1] != 2));
dp[i + 1][j][k] = min(dp[i + 1][j][k], dp[i][j][k] + (a[i + 1] != 3));
}
}
}
if (dp[n][sum][sum] == inf)
{
cout << -1 << endl;
}
else
cout << dp[n][sum][sum] << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号