树形dp

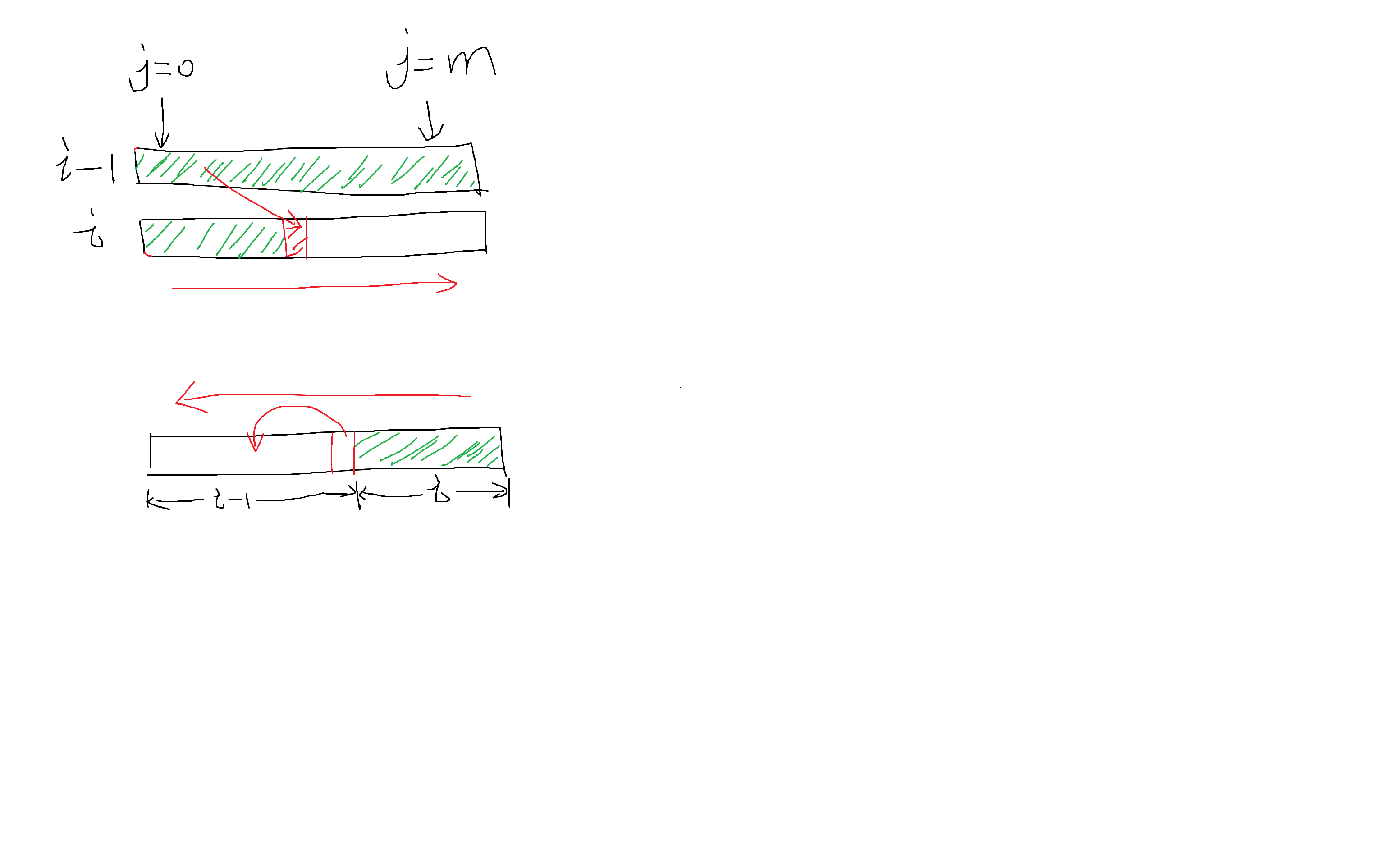
\(fa[u][i][j]\) 表示以 \(u\) 点为根的子树，已经遍历了根为\(u\)的子树的前\(i\)棵子树，选了\(j\)门课程（\(j\)个结点）的最大学分。伪代码如下

for u // 自下而上的遍历
  for i
    for j
      // 枚举当前的分组里面选哪一个物品
      for k from 0 to sz[v]
        // 这里令fa[v][i - 1][j - k] = fa[v][children[v]][j - k]
        fa[u][i][j] = max(fa[u][i-1][j], fa[v][children[v]][j - k])

点击查看代码

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <memory>
#include <numeric>
#include <queue>
#include <set>
#include <typeinfo>
#include <unordered_map>
#include <vector>
// #include "B.h"

using namespace std;

typedef long long ll;

int n;
int head[6004], cnt, par[6004][2];

struct E{
    int to, next;
};

E e[6004];

void add(int u, int v) {
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt++;
}

void dfs(int c) {
  for (int i = head[c]; i != -1; i = e[i].next) {
    int v = e[i].to;
    dfs(v);
    par[c][1] += par[v][0];
    par[c][0] += max(par[v][0], par[v][1]);
  }
}

int happy[6004], vis[6004];

int main() {
  
  cin >> n;
  
  for (int i = 1; i <= n; ++i) {
    cin >> par[i][1];
  }


  std::fill(head, head + n + 1, -1);
  for (int i = 1; i <= n - 1; ++i) {
    int u, v;
    cin >> u >> v;
    add(v, u);
    vis[u] = 1;
  }

  int root = 1;
  for (int i = 1; i <= n; ++i) {
    if (!vis[i]) {
      root = i;
      break;
    }
  }
  dfs(root);
  cout << max(par[root][0], par[root][1]) << endl;
}

最大子树和
有点像最大连续子段和，对于一个当前结点的一个子结点，看以这个子节点为根的子树且包含这个子节点的最大连续字段和是不是大于0，大于0就把这个子树里面的最大值加入当前的最大值集合。

点击查看代码

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <memory>
#include <numeric>
#include <queue>
#include <set>
#include <typeinfo>
#include <unordered_map>
#include <vector>
// #include "B.h"

using namespace std;

typedef long long ll;

const int N = 16003;

ll n, q, score[N], vis[N];
ll head[N], cnt, fa[N], ans;

struct E{
    int to, next, w;
};

E e[N * 2];

void add(int u, int v, int w) {
    e[cnt].to = v;
    e[cnt].w = w;
    e[cnt].next = head[u];
    head[u] = cnt++;
}

void dfs(int c) {
  fa[c] = score[c];
  vis[c] = 1;
  for (int i = head[c]; i != -1; i = e[i].next) {
    int v = e[i].to;
    if (vis[v]) continue;
    dfs(v);
    fa[c] += max(fa[v], 0ll);
  }
  ans = max(ans, fa[c]);
}

int main() {
  cin >> n;

  for (int i = 1; i <= n; ++i)
    cin >> score[i];

  std::fill(head, head + n + 1, -1);
  for (int i = 1; i <= n - 1; ++i) {
    int u, v;
    cin >> u >> v;
    add(u, v, 1);
    add(v, u, 1);
  }
  ans = score[1];
  dfs(1);
  cout << ans << endl;
}

树形背包

Luogu 选课

点击查看代码

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <memory>
#include <numeric>
#include <queue>
#include <set>
#include <typeinfo>
#include <unordered_map>
#include <vector>
// #include "B.h"

using namespace std;

typedef long long ll;

int n, m, score[304], vis[304];
int head[304], cnt, fa[304][304];

struct E{
    int to, next;
};

E e[6004];

void add(int u, int v) {
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt++;
}

int dfs(int c) {
  int p = 1;
  fa[c][1] = score[c];
  for (int i = head[c]; i != -1; i = e[i].next) {
    int v = e[i].to;
    int sz = dfs(v);
    for (int j = min(p, m + 1); j >= 1; j--) {  //由于是01背包，所以要倒序DP, 实际上就是使用了滚动数组
      for (int k = 1; k + j <= m + 1 && k <= sz; ++k) {
        fa[c][j + k] = max(fa[c][j + k], fa[c][j] + fa[v][k]);
      }
    }
    p += sz;
  }
  return p;
}

int main() {
  cin >> n >> m;

  std::fill(head, head + n + 1, -1);
  for (int i = 1; i <= n; ++i) {
    int s, k;
    cin >> k >> score[i];
    add(k, i);
  }
  dfs(0);
  cout << fa[0][m + 1] << endl;
}

Luogu 二叉苹果树

点击查看代码

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <memory>
#include <numeric>
#include <queue>
#include <set>
#include <typeinfo>
#include <unordered_map>
#include <vector>
// #include "B.h"

using namespace std;

typedef long long ll;

int n, q, score[304], vis[304];
int head[304], cnt, fa[304][304];

struct E{
    int to, next, w;
};

E e[6004];

void add(int u, int v, int w) {
    e[cnt].to = v;
    e[cnt].w = w;
    e[cnt].next = head[u];
    head[u] = cnt++;
}

void dfs(int cur) {
  vis[cur] = 1;
  for (int i = head[cur]; i != -1; i = e[i].next) {
    int v = e[i].to, w = e[i].w;
    if (vis[v]) continue;
    
    dfs(v);

    // j 的上界应该是前面遍历过的子树的和
    for (int j = q; j > 0; j--) {
      // k 的上界应该是当前子树的上界
      for (int k = 0; k < j; ++k)
        fa[cur][j] = max(fa[cur][j], fa[cur][j - k - 1] + fa[v][k] + w); 
    }
  }
}

int main() {
  cin >> n >> q;

  std::fill(head, head + n + 1, -1);
  for (int i = 1; i <= n - 1; ++i) {
    int u, v, w;
    cin >> u >> v >> w;
    add(u, v, w);
    add(v, u, w);
  }
  dfs(1);
  cout << fa[1][q] << endl;
}

reference

posted @ 2023-04-26 16:10 o0yo 阅读(34) 评论(0) 收藏举报

刷新页面返回顶部

o0yo

树形dp

树形dp

树形背包

reference

公告