反悔贪心学习笔记

本文仅用于笔者关于反悔贪心的学习笔记，反悔贪心是笔者在一场　$div３$　中遇到的问题，故来学习一番

本篇文章概念部分来源于【学习笔记】反悔贪心 - Koshkaaa (cnblogs.com)
但是对于题目讲解以及贪心策略思路讲解均由笔者著，另加了部分例题作为参考

什么是反悔贪心？

贪心本身是没有反悔操作的，贪心求的就是当前的最优解。但当前的最优解有可能是局部最优解，而不是全局最优解，这时候就要进行反悔操作。

另外的来自蒟蒻dalao的解释：

 

众所周知，正常的贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。也就是说我们的每一步都是站在当前产生的局面上所作出的最好的选择，是没有反悔操作的。

不加反悔的一直朝着当前局面的最优解走很可能导致我们被困在局部的最优解而无法到达全局的最优解，就好像我们爬山就只爬到了一座山的山顶却没有到整片山的最高处：

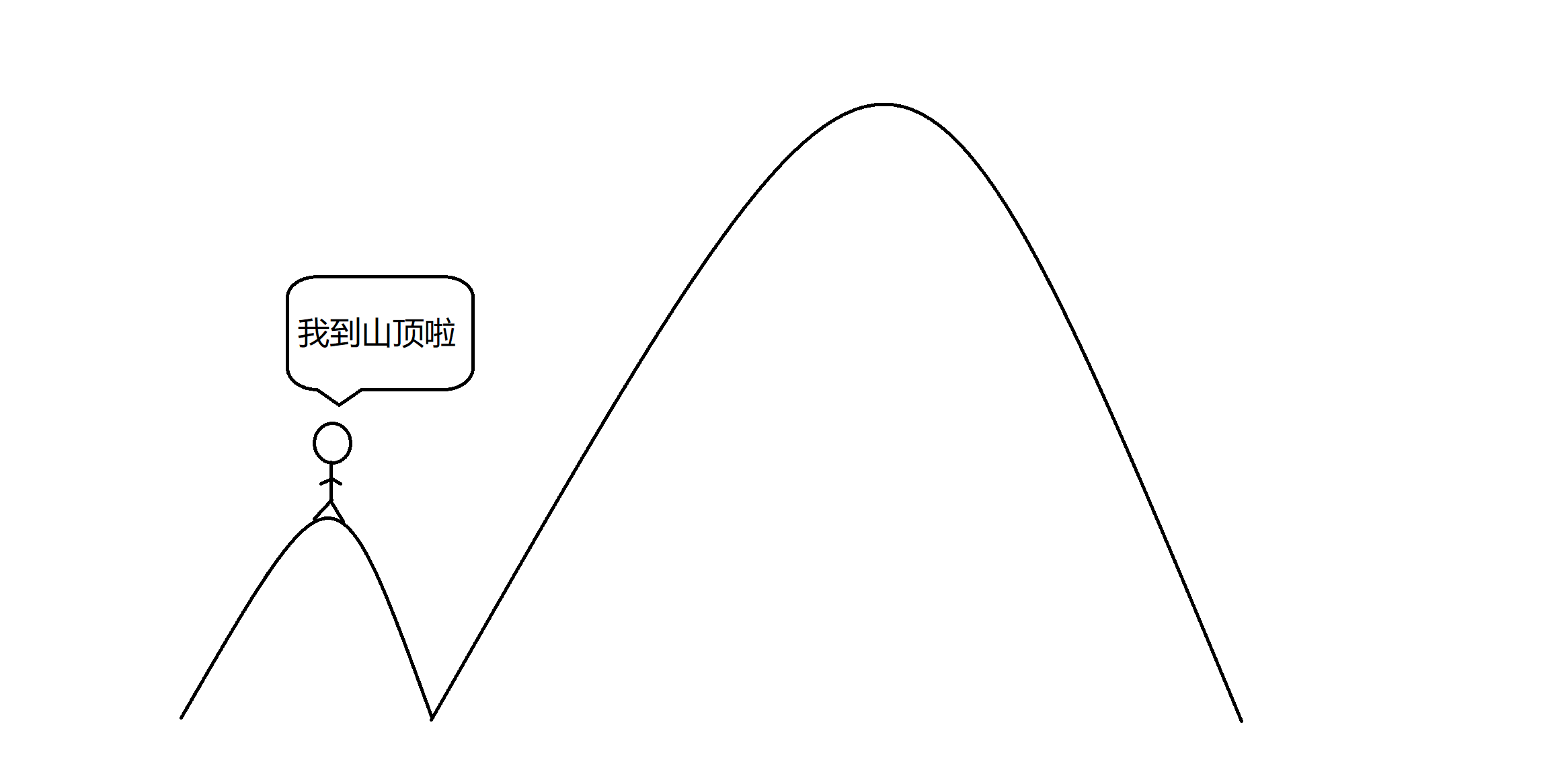
 但是反悔贪心允许我们在发现现在不是全局最优解的情况下回退一步或若干步采取另外的策略去取得全局最优解。就好像我们站在的一座山的山峰上，看到了还有比我们现在所在位置还高的山峰，那我们现在就肯定不是在最高的地方了，这时我们就反悔——也就是下山再爬上那座更高的山：

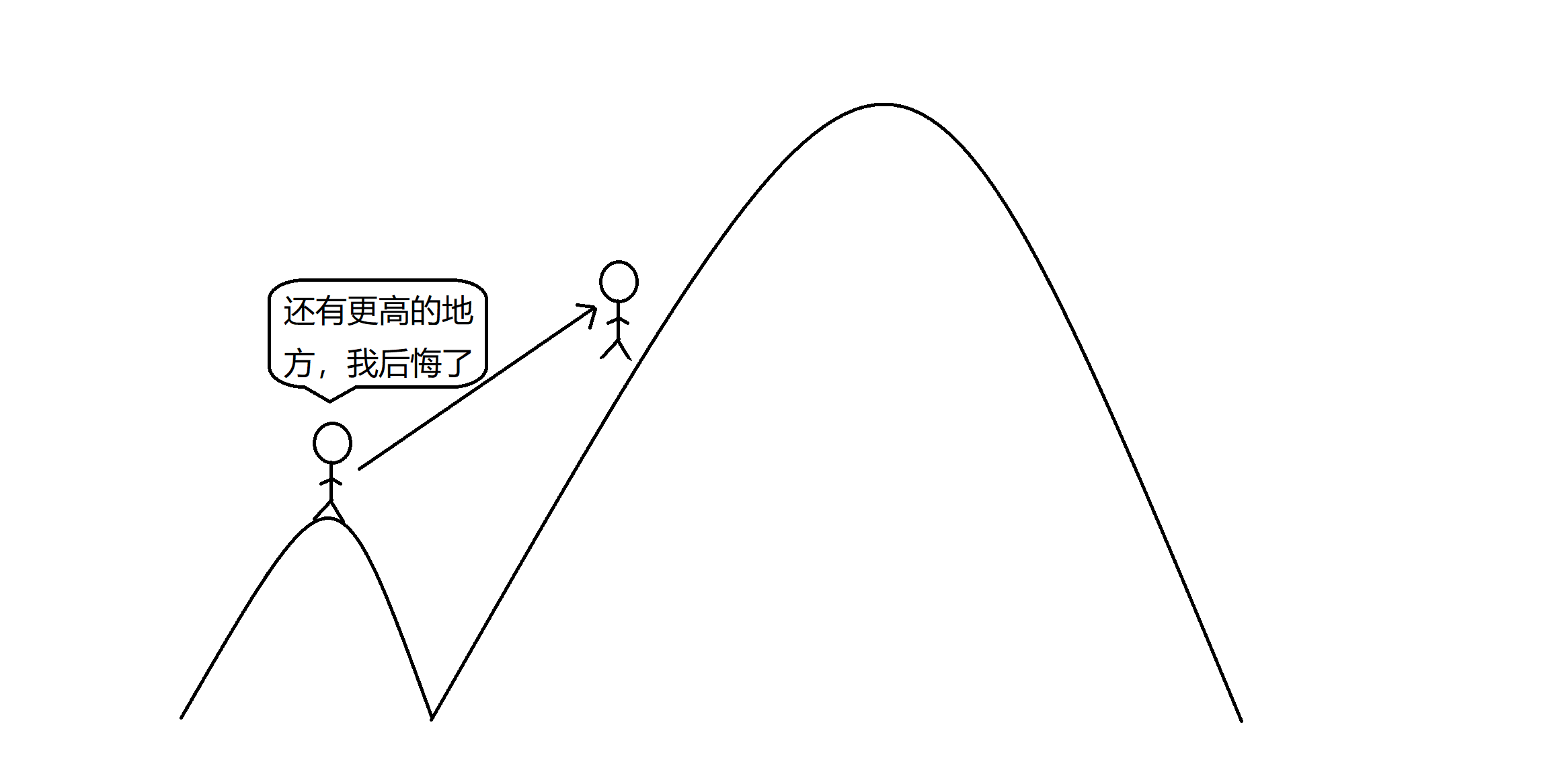
 这就是反悔贪心的大致思路。根据反悔记录操作的不同，反悔贪心又分为反悔堆和反悔自动机。

 

总的来说：反悔操作指的是这一步的贪心不是全局最优解，我们就退回去一步（人工或自动判断），换一种贪心策略。按照判断方式的不同可以分为反悔自动机和反悔堆两种方法。

1. 反悔自动机：

   即设计一种反悔策略，使得随便一种贪心策略都可以得到正解。

   基本的设计思路是：每次选择直观上最接近全局最优解的贪心策略，若发现最优解不对，就想办法自动支持反悔策略。（这就是自动机的意思）

   具体题目具体分析。一般需要反悔自动机的题都是通过差值巧妙达到反悔的目的。

2. 反悔堆：

   即通过堆（大根堆、小根堆）来维护当前贪心策略的最优解，若发现最优解不对，就退回上一步，更新最优解。

   由于堆的性质，使得堆的首数据一定是最优的，这就可以实现快速更新最优解。

例题以及代码

反悔堆

用时一定模型

USACO09OPEN 工作调度Work Scheduling

Description:

有 \(n\) 项工作，每 ii 项工作有一个截止时间 \(D_i\) ，完成每项工作可以得到利润 \(P_i\) ，求最大可以得到多少利润。

Method:

尽管这道题直接理解会感觉简单，实则不然

反悔贪心：

首先根据截止时间排个序，这样方便处理

记录当前的时间，这里设为 $now$ ，那么显然工作一个任务自增即可，在遍历的过程中无非这两种情况：

１：当前时间小于截止时间，那么直接完成任务自增即可，并且把这个工作的价值计入小根堆中

２：当前时间已经大于等于截止时间，那么由于前面的乱做任务可能导致答案小于最佳答案，此时考虑这样一种情况：显然的，小根堆中的任务均是在当前时间之前完成的，且每个任务要求的完成时间都是一个单位时间，那么此时可以放弃前面的一个任务，然后去做这个任务，这样任务数不会变，并且当前时间也不会变，因为两个任务互相抵消，由于已经排过序了，所以小根堆中的任务一定在当前时间之前且符合当前时间小于截止时间，故这样贪心是正确的

 

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10,mod=1e9+7;
signed main()
{
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n; cin>>n;
    priority_queue<int,vector<int>,greater<int>>que;
    vector<pair<int,int>>v;
    for(int i=1;i<=n;i++){
        int d,p; cin>>d>>p;
        v.push_back({d,p});
    }
    sort(v.begin(),v.end());
    int now=0,res=0;
    for(auto [x,y]:v){         
        if(x>now) res+=y,now++,que.push(y);
        else if(!que.empty()&&y>que.top())
            res+=(y-que.top()),que.pop(),que.push(y);
    }
    cout<<res;
    return 0;
}

 

价值一定模型

模型总结来自蒟蒻dalao，万分感谢！

Description:

我们再来考虑这样一个问题，我们有 \(n\) 个任务( \(n≤1e5\) )，并且每个任务都有两个属性——截止日期和完成耗时。在截止日期前完成任务就可以得到这个任务产生的价值。在同一时间我们只能去做一个任务。所有任务的价值都是一样的，问我们最后最多能完成多少个任务。

算法讲解

有了刚刚那题的基础，我们也很容易可以考虑到反悔贪心的反悔堆模型上。由于我们需要反悔操作，而反悔操作是建立我们能够反悔——不做之前决定做的任务而去做当今决定做的任务，所以首先我们肯定还是要按照截止日期从小到大进行排序。

在我们上面讲到的用时一定的模型中，我们用堆维护“性价比”最低的任务也就是我们价值最低的任务用于反悔操作。在这个问题中，我们同样用堆去维护“性价比”最低的任务。由于每个任务的价值是一定的，所以我们性价比最低的任务就是耗时最长的任务，如果我们不做耗时比较长的任务去做耗时比较短的任务，我们就能留下更多的时间给后面的任务，又由于每个任务的价值是一样的，所以这样做的正确性也是显然的。

所以具体来说我们就开一个大根堆维护已选任务的时间，堆顶就是耗时最长的任务。我们顺次考虑排序后的每个任务，当前决定要做的任务的总耗时加上现在这个任务的耗时小于等于现在这个任务的截止时间，那我们就直接做，把现在这个任务丢进堆里，总耗时加上现在这个任务的耗时就可以了。但如果当前决定要做的任务的总耗时加上现在这个任务的耗时大于现在这个任务的截止时间呢，我们就考虑是否进行反悔操作替换决定做的任务。我们看一看堆顶任务的耗时和现在这个任务的耗时，如果堆顶任务的小那就不替换；如果当前任务的耗时小，我们就用当前任务替换掉堆顶任务就好啦。

模板代码

这道题也是有模板题的，题目是[JSOI2007]建筑抢修，下面附上模板代码：

接下来讲下贪心思路：

本质上和上一题其实是一样的，首先还是根据时间进行排序，对于每个任务，还是能完成就完成，完成不了的，我们考虑如何反悔，由于修哪个都是价值加１，所以我们要选择修的时间短的，这样我们的任务时长才会短，任务时长短，那么任务时长＋抢修时间就短，就可能在更多建筑的截止时间内进行抢修，所以我们要在价值不变的情况下尽可能的减小我们的任务时间即可

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10, mod = 1e9 + 7;
signed main()
{
    std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    vector<pair<int, int>> v;
    for (int i = 1; i <= n; i++)
    {
        int t1, t2;
        cin >> t1 >> t2;
        v.push_back({t1, t2});
    }
    auto cmp = [&](pair<int, int> a, pair<int, int> b) -> bool
    {
        return a.second < b.second;
    };
    sort(v.begin(), v.end(), cmp);
    priority_queue<int> que;
    int res = 0, now = 0;
    for (auto [x, y] : v)
    {
        if (now + x < y)
            now += x, res++, que.push(x);
        else if (!que.empty() && x < que.top())
            now -= (que.top() - x), que.pop(), que.push(x);
    }
    cout << res << '\n';
    return 0;
}

Problem - G - Codeforces

很典的一道题，就在 $div3$ 的最后一题，哈哈，和上题的性质一样，价值一样，我们肯定要选择花钱少的，这样我们兜里的钱就更多，就有可能买更多的快乐值

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10, mod = 1e9 + 7;
void solve()
{
    int m, x;
    cin >> m >> x;
    priority_queue<int> que;
    int res = 0, have = 0;
    for (int i = 1; i <= m; i++)
    {
        int c; cin >> c;
        if (have >= c)
            que.push(c), res++, have -= c;
        else if (!que.empty() && c < que.top())
            have += (que.top() - c), que.pop(), que.push(c);
        have += x;
    }
    cout << res << '\n';
}
signed main()
{
    std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int t;
    cin >> t;
    while (t--)
        solve();
}

反悔自动机

相比于反悔堆，反悔自动机更加高级一点，它能够自动的维护我们反悔的操作，通常适用于带限制的决策问题上。

举例：假如我们有四个数ABCD，AB当中只能选一个，CD当中只能选一个，问我们最后能收获的最大价值是多少。

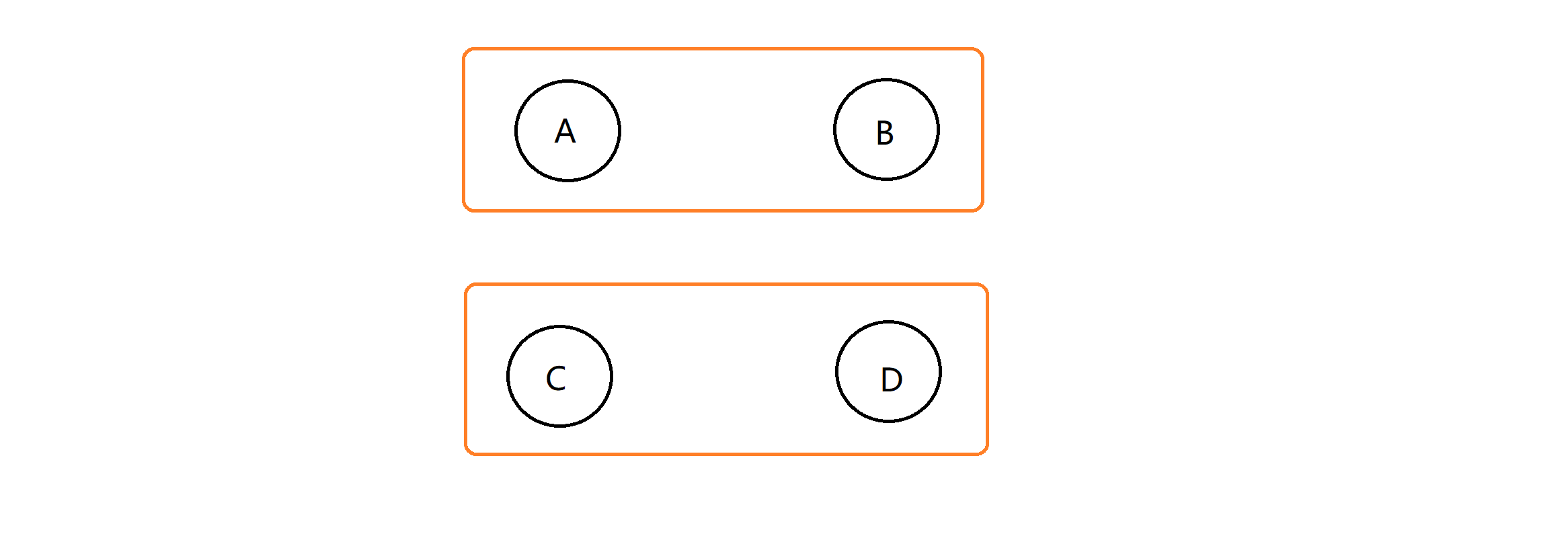
假如刚开始我们选的是AC，那我们就可以把AC先删掉，把的值B变成B-A，D的值变成D-C，接下来的选择不考虑任何束缚。这样如果我们接下来再去选B，那这时我们选的值其实是B-A，加上之前选的A，相当于我们选了B没有选A，这就完成了返回操作——通过修改关联点的值让我们做到不选之前决定选的点而去选现在这个点。

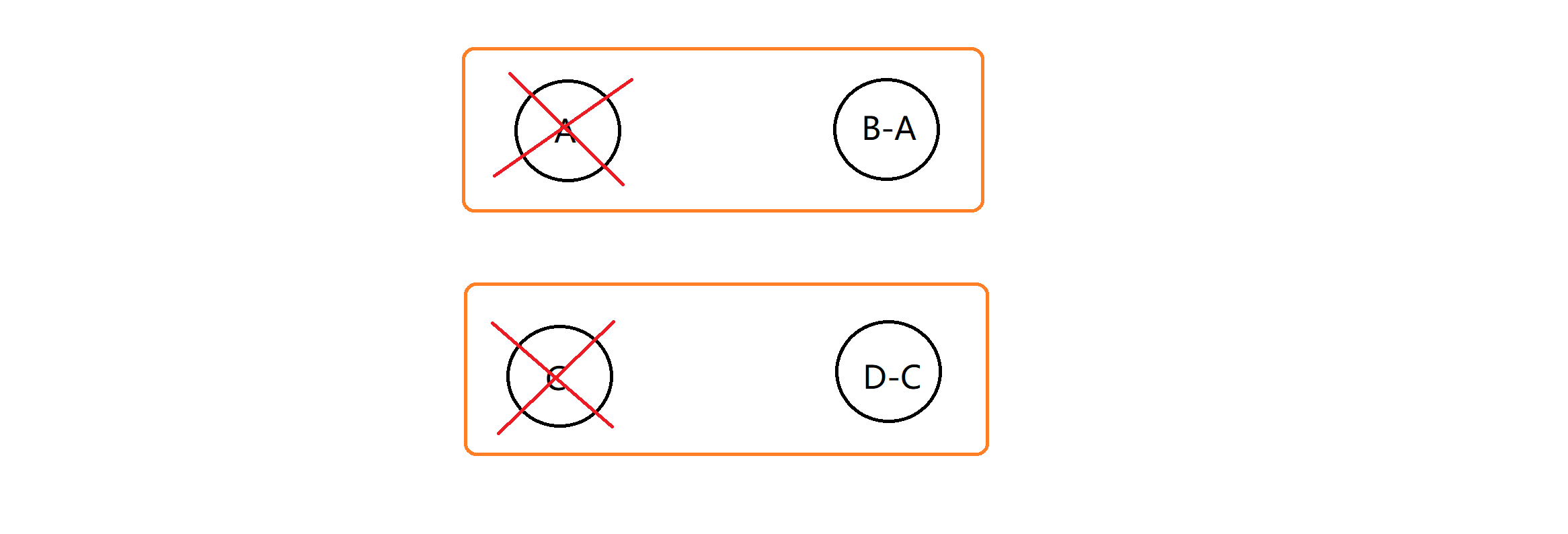
这就是反悔自动机的大致思路。具体的反悔自动机又分为堆反悔自动机和双向链表反悔自动机两种，这样讲可能有点抽象，我们下面通过几个例题来看看反悔自动机的具体运用。

堆反悔自动机

CF865D Buy Low Sell High（堆反悔自动机）

Description:

已知接下来 \(n\) 天的股票价格，每天可以买入当天的股票，卖出已有的股票，或者什么都不做，求 <span class="math inline">\(n\) 天之后最大的利润。

Method：

我们先从简单的贪心开始考虑。首先我们可以贪心地对于每一天 i，如果我们可以卖出，那么贪心的选择之前的价格最小的一天 j，然后若 \(P_j < P_i\) 就可以在 j 天买入一股，然后在第 i 天卖出，这时候就仅需要一个 <code>priority_queue</code> 就可以了。

但是还有一个问题，如何考虑下面这组数据呢？

1 2 5

可以发现，若贪心处理，则仅会在第 1 天买入一股，并在第 2 天卖出，赚到了 1 元。但是若将第 1 天的股票在第 3 天卖出，则可以获得高达 4 元的利润，比原答案不知道高到哪里去了。

---

所以我们尝试去考虑设计一种反悔策略，使所有的贪心情况都可以得到全局最优解。（即设计反悔自动机的反悔策略）

定义 \(C_{buy}\) 为全局最优解中买入当天的价格，<span class="math inline">\(C_{sell}\) 为全局最优解中卖出当天的价格，则：

 

\[C_{sell} - C_{buy} = (C_{sell} -C_i) + (C_i - C_{buy}) \]

 

\(C_i\) 为任意一天的股票价格

即我们买价格最小的股票去卖价格最大的股票，以期得到最大的利润。我们先把当前的价格放入小根堆一次（这次是以上文的贪心策略贪心），判断当前的价格是否比堆顶大，若是比其大，我们就将差值计入全局最优解，再将当前的价格放入小根堆（这次是反悔操作）。相当于我们把当前的股票价格若不是最优解，就没有用，最后可以得到全局最优解。

上面的等式即被称为反悔自动机的反悔策略，因为我们并没有反复更新全局最优解，而是通过差值消去中间项的方法快速得到的全局最优解。

Code:

struct node {
    int value;
    // 重载<号的定义，规定堆为关于价值的小根堆
    bool operator<(const node &b) const {
        if (value > b.value) return true;
        return false;
    }
} a[330000];
priority_queue<node> q;
int n;
ll cnt = 0;

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i].value;

    for (int i = 1; i <= n; ++i) {
        q.push(a[i]);  //用于贪心买价格最小的股票去买价格最大的股票
        //假如当前的股票价格不是最优解
        if (q.size() && q.top().value < a[i].value) {
            cnt += a[i].value - q.top().value;  //将差值计入全局最优解
            // 将已经统计的最小的股票价格丢出去，并执行反悔策略：将当前的股票价格再放入堆中，即记录中间变量（等式中间的Vi)
            q.pop(), q.push(a[i]);
        }
    }
    cout << cnt << "\n";
    return 0;
}

双向链表反悔自动机

BZOJ2151 种树（双向链表反悔自动机）

Description:

有 \(n\) 个位置，每个位置有一个价值。有 <span class="math inline">\(m\) 个树苗，将这些树苗种在这些位置上，相邻位置不能都种。求可以得到的最大值或无解信息。

Method：

先判断无解的情况，我们显然可以发现，若 \(m>\frac{n}2\) ，则是不能在合法的条件下种上 m 棵树的，故按题意输出<code>Error!</code>即可。

假如有解的话，我们可以很轻松的推出贪心策略：在合法的情况下选择最大的价值。

显然上面的策略是错误的，我们选择了最大价值的点，相邻的两个点就不能选，而选择相邻两个点得到的价值可能更大。

考虑如何设计反悔策略。

我们同样用差值来达到反悔的目的。假设有 \(A ，B ，C ，D\) 四个相邻的点（如图）。

\(A\) 点的价值为 <span class="math inline">\(a\) ，其他点同理。若

 

\[a + c > b + d \]

 

则：

 

\[a + c - b > d \]

 

假如我们先选了 \(B\) 点，我们就不能选 <span class="math inline">\(A\) 和 <span class="math inline">\(C\) 两点，这显然是不对的，但我们可以新建一个节点 <span class="math inline">\(P , P\) 点的价值为 $a+c−b $，再删去 <span class="math inline">\(B\) 点。（如图，红色的是删去的点，橙色的新建的点)

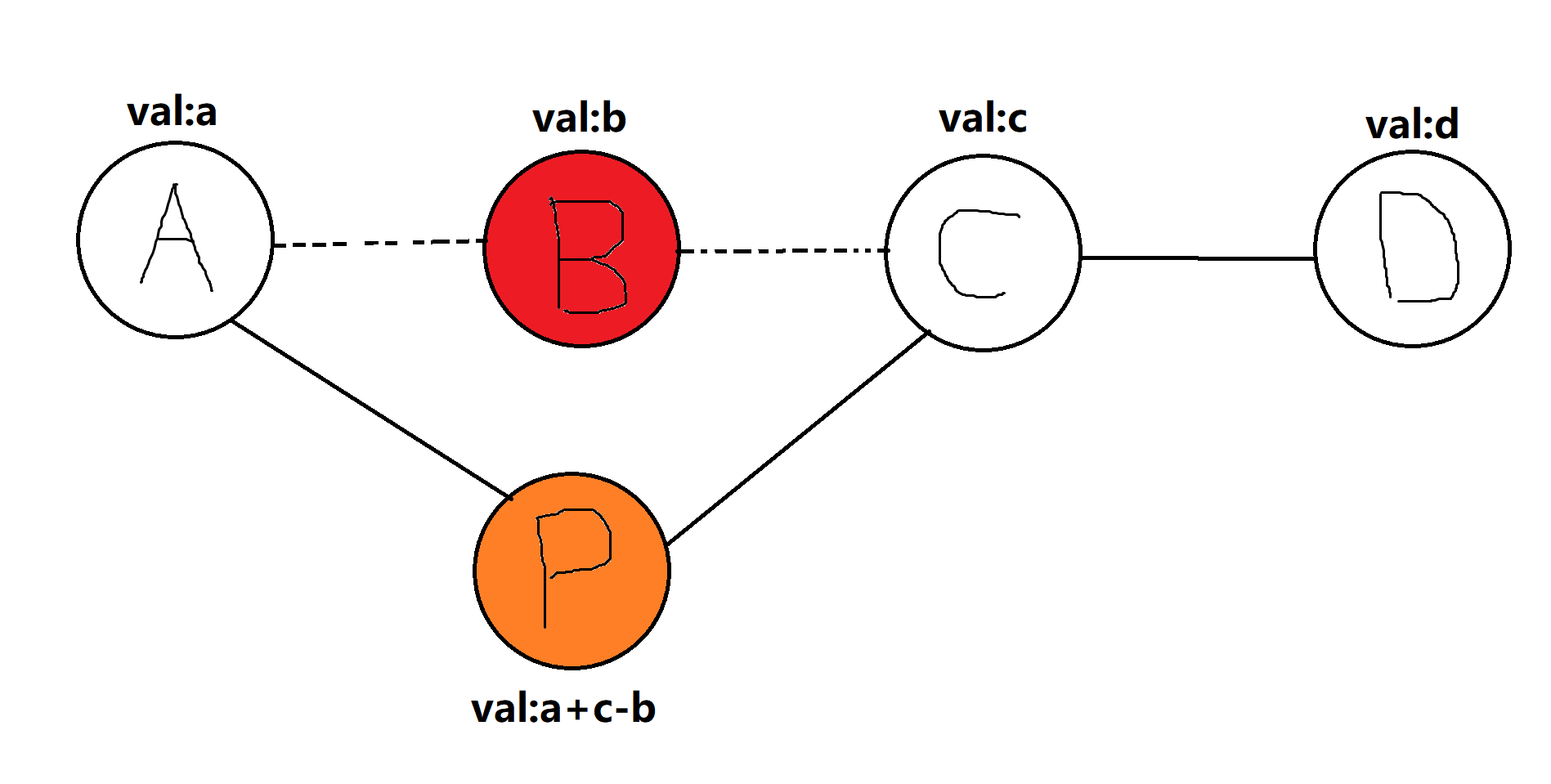
下一次选择的点是 P 的话，说明我们反悔了（即相当于 B 点没有选），可以保证最后的贪心最优解是全局最优解。

如何快速插入 P 点和找出是否选择 P 点呢？我们可以使用双向链表和小根堆，使得最终在 \(O(nlog⁡n)\) 的时间复杂度下快速求出全局最优解.

注意点：

• 一定要记录这个点选没有选过，假如已经选过了，就从堆中丢出去；
• 1 与 n 是相邻的，一定要特判一下；
• 双向链表一定不要写挂了；
• 一定要先将新建的点的价值存入一开始的价值数组，再丢进堆里；（不然会卡数据）

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e6 + 10;
struct node {
    int val, id;
    bool operator<(const node& x) const { return val < x.val; }
} now, x;
ll val[N];              // 价值
ll vis[N], l[N], r[N];  // vis记录是否删除,l、r为双向链表的左右点

int t, n, m;
ll ans = 0;
priority_queue<node> q;
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> val[i];
    while (q.size()) q.pop();

    // 初始化堆
    for (ll i = 1; i <= n; ++i) {
        now.id = i, now.val = val[i];
        vis[i] = 0;
        q.push(now);
    }

    // 处理双向链表
    for (int i = 2; i <= n; ++i) l[i] = i - 1;
    for (int i = 1; i <= n; ++i) r[i] = i + 1;

    l[1] = r[n] = 0;

    for (int i = 1; i <= m; ++i) {
        x = q.top(), q.pop();
        while (vis[x.id] == 1) {  //找到一个没有被删除的值最大的点
            x = q.top(), q.pop();
        }

        if (x.val < 0) break;
        ans += x.val;
        if (l[x.id] != 0) vis[l[x.id]] = 1;  //删除左边的点
        if (r[x.id] != 0) vis[r[x.id]] = 1;  //删除右边的点

        if (l[x.id] != 0 && r[x.id] != 0) {
            now.id = x.id;
            now.val = val[x.id] = val[l[x.id]] + val[r[x.id]] - val[x.id];

            r[l[l[x.id]]] = x.id;
            l[x.id] = l[l[x.id]];
            l[r[r[x.id]]] = x.id;
            r[x.id] = r[r[x.id]];
            q.push(now);
        } else if (l[x.id])
            r[l[l[x.id]]] = 0;
        else
            l[r[r[x.id]]] = 0;
    }
    cout << ans << "\n";
    return 0;
}