Kruskal重构树

Kruskal重构树,即与瓶颈树类似,kurskal重构树的特性是,任意两点之间的简单路径种的(最大或最小)边权值为其最近公共祖先

Kruskal算法
首先给出一张有向图，让我们求最小生成树（用总权值最小的一些边的集合，使得所有点都能互通，很明显n个点会有n-1条边）

 

 

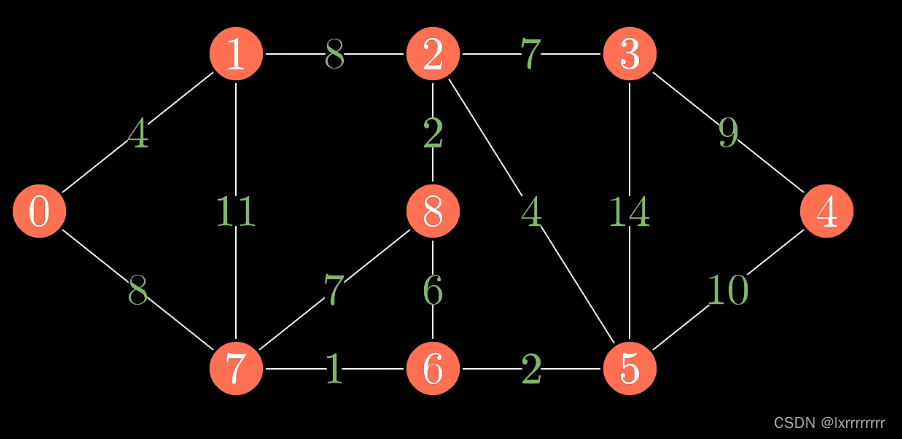
kruskal算法思想是先把所有的边按权值大小排序，得到这个样子

 

 

然后从小往大依次取边，如果加上这条边和之前的边构成了环，就舍弃这条边，不然就加上，直至取得n-1条边，构成一棵树

例如此图，我们按照权值加完前四条边

 

 

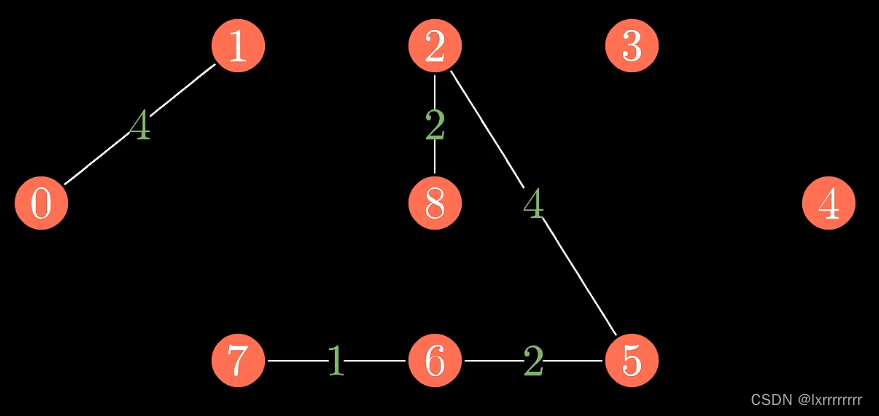
在加入第五条边时，我们发现原图出现了环，我们就舍弃这条边

 

 

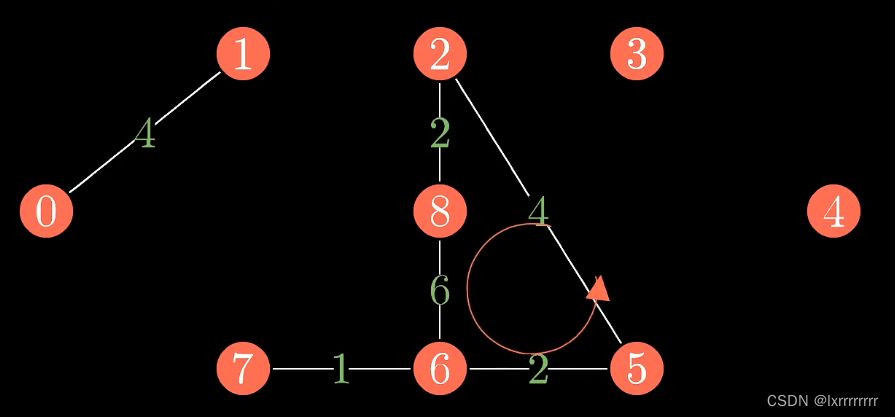
就这样一直加边，直至构成一棵完整的树

 

 

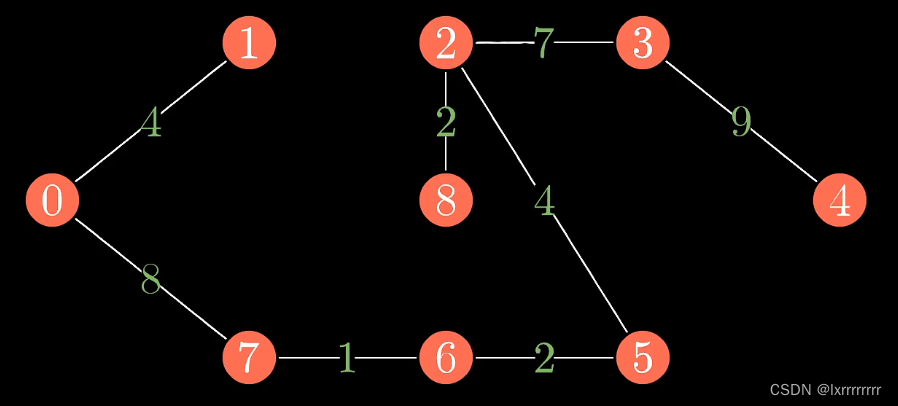
这就是kruskal算法的

Kruskal重构树
那么什么又是kruskal重构树呢？

kruskal重构树其实就是把这张图重建成一个二叉树，原图中所有的叶子节点都为原图中的点

其他点都有一个点权w，代表从左集合到右集合的路径，由于重构树是在kruskal的基础上完成的，所以我们必然可以得到一个自下而上点权不降的二叉树

比如我们还用上图距离，建一颗重构树

首先我们合并6，7两个集合，把他们两个连接到一个虚点上，该点权值为他们的边权

 

 

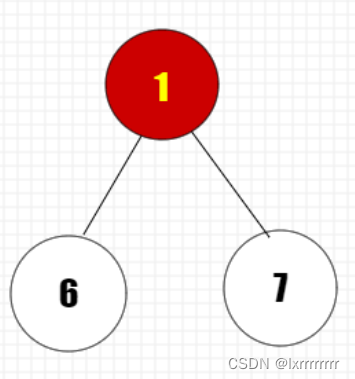
（红色代表虚点，白色代表原图的点）

然后我们依次2-8 ， 5-6

 

 

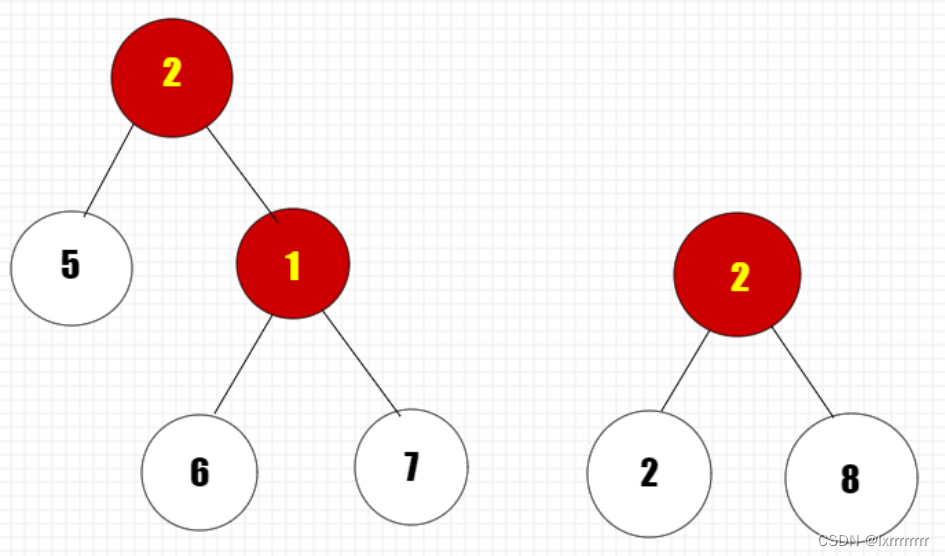
就这样把这颗二叉树建完

 

 

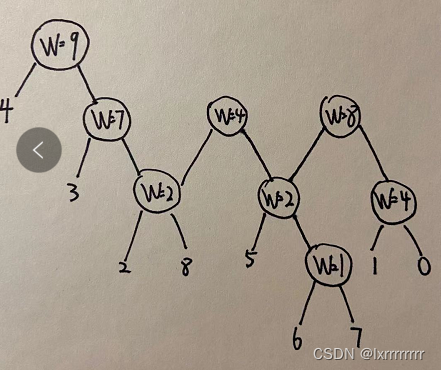
最后重构树大概长这样

这棵树有很多独特的性质

就比如我们想知道从节点2到7路径的最大边权是多少，其实就是他们公共祖先这个虚点的点权值

再比如我们想知道从某个点出发，给出一个值，在通过所有边的权值都小于等于这个值时，我们走过多少个点，其实就等于这个点一直往上面找，找到最后一个小于等于这个值的虚点，他的子树的点我们都是可以通过的（因为从上到下点权不上升）

以上这种问题我们都可以通过在重构树上倍增的方式，把时间复杂度压到logn 

转载: Kruskal重构树详解-CSDN博客

 

例题:

P9235 [蓝桥杯 2023 省 A] 网络稳定性 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

首先,我们需要重构一棵kruskal最大树,那么由于重构书的性质,我们先把最大的连接上,然后依次递减连接,这样我们走得就是最大生成树,对于任意两点之间的距离,其lca肯定是简单路径中边权最小得最大值,因为我们排过序了

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10,mod=1e9+7;
int son[N],fa[N],sz[N],top[N],dep[N],p[N],w[N];
vector<int>g[N];
struct node{
    int u,v,w;
    bool operator<(const node&W)const{
        return w>W.w;
    }
}edge[N];
int find(int x){
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}
void dfs1(int u){
    sz[u]=1,dep[u]=dep[fa[u]]+1;
    for(auto x:g[u]){
        if(x==fa[u]) continue;
        fa[x]=u;
        dfs1(x);
        sz[u]+=sz[x];
        if(sz[son[u]]<sz[x]) son[u]=x;
    }
}
void dfs2(int u,int h){
    top[u]=h;
    if(son[u]) dfs2(son[u],h);
    for(auto x:g[u]){
        if(x==fa[u]||x==son[u]) continue;
        dfs2(x,x);
    }
}
int lca(int a,int b){
    while(top[a]!=top[b]){
        if(dep[top[a]]>dep[top[b]]) a=fa[top[a]];
        else b=fa[top[b]];
    }
    return dep[a]>dep[b]?b:a;
}
signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n,m,q; cin>>n>>m>>q;
    for(int i=1;i<=2*n;i++) p[i]=i;
    for(int i=1;i<=m;i++){
        int a,b,c; cin>>a>>b>>c;
        edge[i]={a,b,c};
    }
    sort(edge+1,edge+1+m);
    int cnt=n;
    for(int i=1;i<=m;i++){
        int u=find(edge[i].u),v=find(edge[i].v),val=edge[i].w;
        if(u==v) continue;
        w[++cnt]=val,p[u]=p[v]=find(cnt);
        g[cnt].push_back(u),g[cnt].push_back(v);
    }
    for(int i=cnt;i>=cnt-1;i--)
        if(!son[i]||!top[i]) dfs1(i),dfs2(i,i);
    while(q--){
        int a,b; cin>>a>>b;
        if(find(a)!=find(b)) cout<<-1<<endl;
        else cout<<w[lca(a,b)]<<endl;
    }
}

P2245 星际导航 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

这个就是求最小生成树kurskal重构树了

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10,mod=1e9+7;
struct node{
    int u,v,w;
    bool operator<(const node&W)const{
        return w<W.w;
    }
}edge[N];
int w[N],son[N],sz[N],fa[N],top[N],dep[N],p[N];
vector<int>g[N];
int find(int x){
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}
void dfs1(int u){
    sz[u]=1,dep[u]=dep[fa[u]]+1;
    for(auto x:g[u]){
        if(x==fa[u]) continue;
        fa[x]=u;
        dfs1(x);
        sz[u]+=sz[x];
        if(sz[son[u]]<sz[x]) son[u]=x;
    }
}
void dfs2(int u,int h){
    top[u]=h;
    if(son[u]) dfs2(son[u],h);
    for(auto x:g[u]){
        if(x==fa[u]||x==son[u]) continue;
        dfs2(x,x);
    }
}
int lca(int a,int b){
    while(top[a]!=top[b]){
        if(dep[top[a]]>dep[top[b]]) a=fa[top[a]];
        else b=fa[top[b]];
    }
    return dep[a]>dep[b]?b:a;
}
signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n,m; cin>>n>>m;
    for(int i=1;i<=2*n;i++) p[i]=i;
    for(int i=1;i<=m;i++){
        int a,b,c; cin>>a>>b>>c;
        edge[i]={a,b,c};
    }
    sort(edge+1,edge+1+m);
    int cnt=n;
    for(int i=1;i<=m;i++){
        int u=find(edge[i].u),v=find(edge[i].v),val=edge[i].w;
        if(u==v) continue;
        w[++cnt]=val,p[u]=p[v]=find(cnt);
        g[cnt].push_back(u),g[cnt].push_back(v);
    }
    for(int i=cnt;i>=cnt-1;i--)
        if(!son[i]||!top[i]) dfs1(i),dfs2(i,i);
    int q; cin>>q;
    while(q--){
        int a,b; cin>>a>>b;
        if(find(a)!=find(b)) cout<<"impossible"<<endl;
        else cout<<w[lca(a,b)]<<endl;
    }
//    for(int i=n+1;i<=cnt;i++){
//        cout<<i<<endl;
//        for(auto x:g[i]) cout<<x<<' ';
//        cout<<endl;
//    }
}

 Problem - H - Codeforces

维护一下父节点的值,然后倍增的跳就行,不要问我为什么要倍增,因为会超时呜呜呜

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+10,mod=1e9+7;
struct node{
    int u,v,w;
    bool operator<(const node&W)const{
        return w<W.w;
    }
}edge[N];
int dp[N][21],a[2*N],p[N],w[N],val[N];
vector<int>g[N];
int find(int x){
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}
void dfs(int u,int fa){
    dp[u][0]=fa;
    for(int i=1;i<=20;i++) dp[u][i]=dp[dp[u][i-1]][i-1];
    for(auto x:g[u]){
        if(x==fa) continue;
        dfs(x,u);
        a[u]+=a[x];
    }
}
signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n,m,q; cin>>n>>m>>q;
    for(int i=1;i<=2*n;i++) p[i]=i;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=m;i++){
        int x,y,z; cin>>x>>y>>z;
        edge[i]={x,y,z};
    }
    sort(edge+1,edge+1+m);
    int cnt=n;
    for(int i=1;i<=m;i++){
        int u=find(edge[i].u),v=find(edge[i].v);
        if(u==v) continue;
        w[++cnt]=edge[i].w,p[u]=p[v]=cnt;
        g[cnt].push_back(u),g[cnt].push_back(v);
    }
    dfs(cnt,0),w[0]=1e18;
    while(q--){
        int c,k; cin>>c>>k;
        int res=k+a[c];
        while(c!=cnt){
            int x=c;
            for(int i=20;i>=0;i--)
                if(w[dp[c][i]]<=res) c=dp[c][i];
            if(x==c) break;
            res=a[c]+k;
        }
        cout<<res<<endl;
    }
}

 P1967 [NOIP2013 提高组] 货车运输 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10,mod=1e9+7;
int sz[N],dep[N],top[N],son[N],fa[N],w[N],p[N];
vector<int>g[N];
struct node{
    int u,v,w;
    bool operator<(const node&W)const{
        return w>W.w;
    }  
}edge[N];
int find(int x){
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}
void dfs1(int u){
    sz[u]=1,dep[u]=dep[fa[u]]+1;
    for(auto x:g[u]){
        if(x==fa[u]) continue;
        fa[x]=u;
        dfs1(x);
        sz[u]+=sz[x];
        if(sz[x]>sz[son[u]]) son[u]=x;
    }    
}
void dfs2(int u,int h){
    top[u]=h;
    if(son[u]) dfs2(son[u],h);
    for(auto x:g[u]){
        if(x==fa[u]||x==son[u]) continue;
        dfs2(x,x);
    }
}
int lca(int a,int b){
    while(top[a]!=top[b]){
        if(dep[top[a]]>dep[top[b]])
            a=fa[top[a]];
        else b=fa[top[b]];
    }
    return dep[a]>dep[b]?b:a;
}
signed main()
{
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n,m; cin>>n>>m;
    for(int i=1;i<=m;i++){
        int a,b,c; cin>>a>>b>>c;
        edge[i]={a,b,c};
    }
    sort(edge+1,edge+1+m);
    for(int i=1;i<=4*n;i++) p[i]=i;
    int cnt=n;
    for(int i=1;i<=m;i++){
        int u=find(edge[i].u),v=find(edge[i].v);
        if(u==v) continue;
        cnt++,p[u]=p[v]=find(cnt);
        w[cnt]=edge[i].w;
        g[cnt].push_back(u),g[cnt].push_back(v);
    }
    // dfs1(cnt),dfs2(cnt,cnt);
    // cout<<cnt<<'\n';
    for(int i=cnt;i>=n+1;i--)
        if(!son[i]||!top[i]) dfs1(i),dfs2(i,i);
    int q; cin>>q;
    while(q--){
        int a,b; cin>>a>>b;
        int res=w[lca(a,b)];
        cout<<(res?res:-1)<<'\n';
    }
    return 0;
}