Forever Winter

 Forever Winter

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A snowflake graph is generated from two integers x and y, both greater than 11, as follows:

• Start with one central vertex.
• Connect x new vertices to this central vertex.
• Connect y new vertices to each of these x vertices.

For example, below is a snowflake graph for x=5=5 and y=3=3.

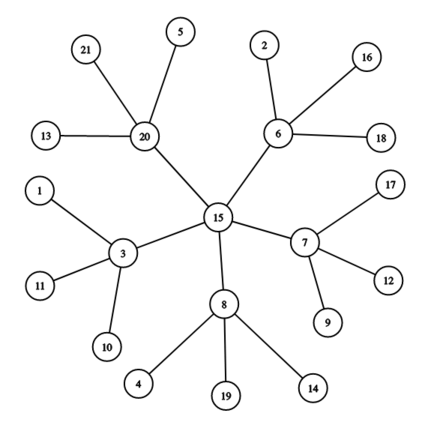
The snowflake graph above has a central vertex 1515, then x=5=5 vertices attached to it (33, 66, 77, 88, and 2020), and then y=3=3 vertices attached to each of those.

Given a snowflake graph, determine the values of x and y.

Input

The first line contains a single integer t (1≤t≤10001≤≤1000) — the number of test cases.

The first line of each test case contains two integers n and m (2≤n≤2002≤≤200; 1≤m≤min(1000,n(n−1)2)1≤≤min(1000,(−1)2)) — the number of vertices and edges in the graph, respectively.

The next m lines each contain two integers each u and v (1≤u,v≤n1≤,≤, u≠v≠) — the numbers of vertices connected by an edge. The graph does not contain multiple edges and self-loops.

It is guaranteed that this graph is a snowflake graph for some integers x and y both greater than 11.

Output

For each test case, on a separate line output the values of x and y, in that order, separated by a space.

Example

input

Copy

3

21 20

21 20

5 20

13 20

1 3

11 3

10 3

4 8

19 8

14 8

9 7

12 7

17 7

18 6

16 6

2 6

6 15

7 15

8 15

20 15

3 15

7 6

1 2

1 3

2 4

2 5

3 6

3 7

9 8

9 3

3 6

6 2

2 1

5 2

2 7

4 3

3 8

output

Copy

5 3
2 2
2 3

Note

The first test case is pictured in the statement. Note that the output 3 5 is incorrect, since x should be output before y.

#include <bits/stdc++.h>
//#define int long long
using namespace std;
const int N=1e5+10,mod=1e9+7;
string s;
int n,t,a[N],f[N],res,num,ans,m;
bool vis;
vector<int>g[500];
int main()
{
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>t;
    while(t--){
        cin>>n>>m;
        memset(f,0,sizeof f);
        for(int i=1;i<=n;i++) g[i].clear();
        res=ans=0;
        for(int i=0;i<m;i++){
            int u,v;
            cin>>u>>v;
            g[v].push_back(u),f[u]++;
            g[u].push_back(v),f[v]++;
        }
        for(int i=1;i<=n;i++){//只需要找到一个所有的子节点都不是1的点就可以
            if(f[i]==1) continue;
            vis=true;
            for(auto v:g[i])
                if(f[v]==1){
                    vis=false;
                    break;
                }
            if(vis){
                res=f[i],ans=f[g[i][0]]-1;
                break;
            }
        }
        cout<<res<<" "<<ans<<endl;;
    }
    return 0;
}