证明三角形中位线定理

证明内容：现有一三角形，定义其任意两条边的中点所连线段为其中位线，试证明其中位线平行于第三边且等于第三边的一半

证明：

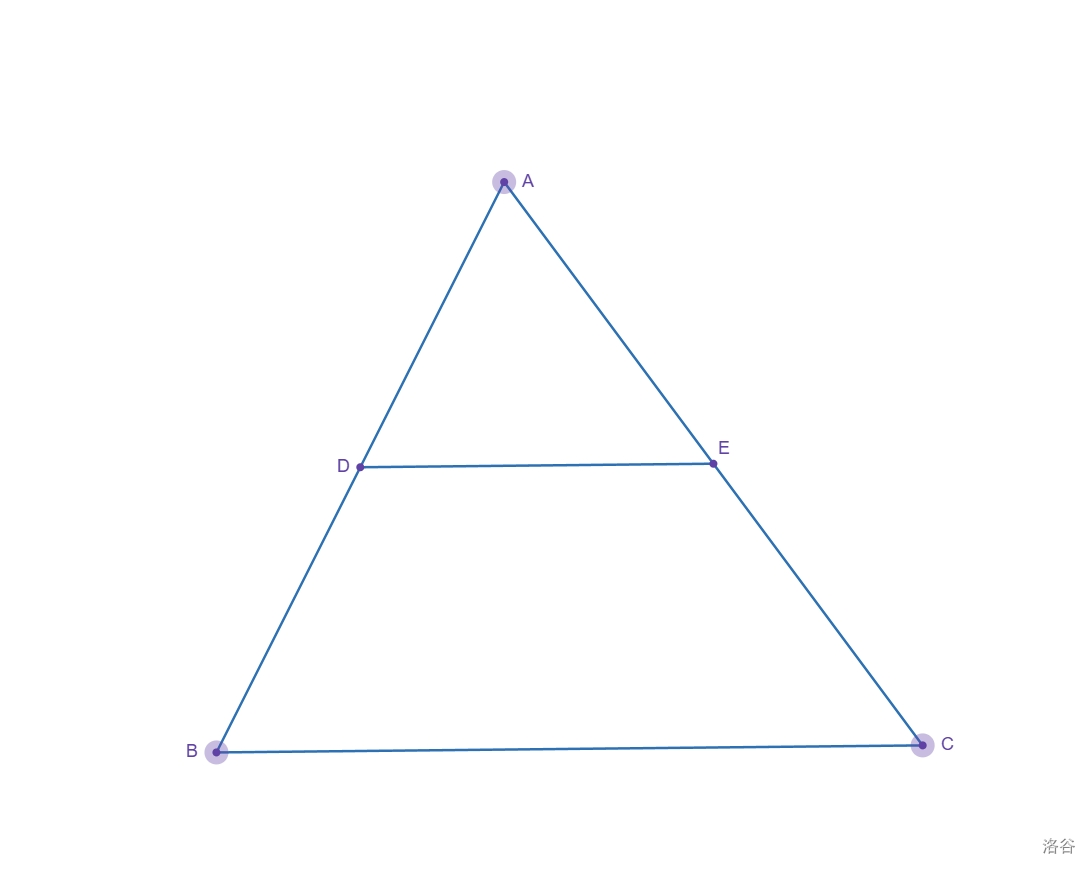
\[现有△ABC，A(x_1,y_1),B(x_2,y_2),C(x_3,y_3) \]

\[∴线段AB中点D(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}),线段BC中点E(\frac{x_1+x_3}{2},\frac{y_1+y_3}{2}) \]

\[\begin{aligned} DE &= \sqrt{(\frac{x_1+x_2}{2}-\frac{x_1+x_3}{2})^2+(\frac{y_1+y_2}{2}-\frac{y_1+y_3}{2})^2}\\ &=\sqrt{(\frac{x_1-x_3}{2})^2+(\frac{y_1-y_3}{2})^2}\\ &=\sqrt{\frac{(x_1-x_3)^2}{4}+\frac{(y_1-y_3)^2}{4}}\\ &=\sqrt{\frac{(x_1-x_3)^2+(y_1-y_3)^2}{4}}\\ &=\frac{\sqrt{(x_1-x_3)^2+(y_1-y_3)^2}}{2} \end{aligned}\]

\[∵B(x_2,y_2),C(x_3,y_3) \]

\[∴BC=\sqrt{(x_1-x_3)^2+(y_1-y_3)^2} \]

\[∴DE=\frac{1}{2}BC \]

\[令直线DE的解析式为y_1=k_1x+b_1,将D,E点坐标代入得: \]

\[\begin{cases} \frac{x_1+x_2}{2}k_1+b_1=\frac{y_1+y_2}{2}①\\ \frac{x_1+x_3}{2}k_1+b_1=\frac{y_1+y_3}{2}② \end{cases}\]

\[①式-②式,得: \]

\[\frac{x_2-x_3}{2}k_1=\frac{y_2-y_3}{2} \]

\[即(x_2-x_3)k_1=y_2-y_3 \]

\[令直线AB的解析式为y_2=k_2x+b_2,将A,B点坐标代入得: \]

\[\begin{cases} x_2k_2+b_2=y_2③\\ x_3k_2+b_2=y_3④ \end{cases}\]

\[③式-④式,得: \]

\[(x_2-x_3)k_2=y_2-y_3 \]

\[∵(x_2-x_3)k_1=y_2-y_3 \]

\[∴k_1=k_2 \]

\[∴DE\parallel AB \]

\[∴证毕 \]