决策树算法原理

转载于：http://www.cnblogs.com/pinard/p/6050306.html （楼主总结的很好，就拿来主义了，不顾以后还是多像楼主学习）

　　　决策树算法在机器学习中算是很经典的一个算法系列了。它既可以作为分类算法，也可以作为回归算法，同时也特别适合集成学习比如随机森林。本文就对决策树算法原理做一个总结，上篇对ID3， C4.5的算法思想做了总结，下篇重点对CART算法做一个详细的介绍。决策树根据一步步地属性分类可以将整个特征空间进行划分，从而区别出不同的分类样本

1. 决策树ID3算法的信息论基础

　　　　机器学习算法其实很古老，作为一个码农经常会不停的敲if, else if, else,其实就已经在用到决策树的思想了。只是你有没有想过，有这么多条件，用哪个条件特征先做if，哪个条件特征后做if比较优呢？怎么准确的定量选择这个标准就是决策树机器学习算法的关键了。1970年代，一个叫昆兰的大牛找到了用信息论中的熵来度量决策树的决策选择过程，方法一出，它的简洁和高效就引起了轰动，昆兰把这个算法叫做ID3。下面我们就看看ID3算法是怎么选择特征的。

　　　　首先，我们需要熟悉信息论中熵的概念。熵度量了事物的不确定性，越不确定的事物，它的熵就越大。具体的，随机变量X的熵的表达式如下：

H(X)=−∑i=1npilogpiH(X)=−∑i=1npilogpi

　　　　其中n代表X的n种不同的离散取值。而pipi代表了X取值为i的概率，log为以2或者e为底的对数。举个例子，比如X有2个可能的取值，而这两个取值各为1/2时X的熵最大，此时X具有最大的不确定性。值为H(X)=−(12log12+12log12)=log2H(X)=−(12log12+12log12)=log2。如果一个值概率大于1/2，另一个值概率小于1/2，则不确定性减少，对应的熵也会减少。比如一个概率1/3，一个概率2/3，则对应熵为H(X)=−(13log13+23log23)=log3−23log2<log2)H(X)=−(13log13+23log23)=log3−23log2<log2).

　　　　熟悉了一个变量X的熵，很容易推广到多个个变量的联合熵，这里给出两个变量X和Y的联合熵表达式：

H(X,Y)=−∑i=1np(xi,yi)logp(xi,yi)H(X,Y)=−∑i=1np(xi,yi)logp(xi,yi)

　　　　有了联合熵，又可以得到条件熵的表达式H(X|Y)，条件熵类似于条件概率,它度量了我们的X在知道Y以后剩下的不确定性。表达式如下： 

H(X|Y)=−∑i=1np(xi,yi)logp(xi|yi)=∑j=1np(yj)H(X|yj)H(X|Y)=−∑i=1np(xi,yi)logp(xi|yi)=∑j=1np(yj)H(X|yj) 

　　　　好吧，绕了一大圈，终于可以重新回到ID3算法了。我们刚才提到H(X)度量了X的不确定性，条件熵H(X|Y)度量了我们在知道Y以后X剩下的不确定性，那么H(X)-H(X|Y)呢？从上面的描述大家可以看出，它度量了X在知道Y以后不确定性减少程度，这个度量我们在信息论中称为互信息，，记为I(X,Y)。在决策树ID3算法中叫做信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大，则越适合用来分类。

　　　　上面一堆概念，大家估计比较晕，用下面这个图很容易明白他们的关系。左边的椭圆代表H(X),右边的椭圆代表H(Y),中间重合的部分就是我们的互信息或者信息增益I(X,Y), 左边的椭圆去掉重合部分就是H(X|Y),右边的椭圆去掉重合部分就是H(Y|X)。两个椭圆的并就是H(X,Y)。

信息熵(Entropy)、信息增益(Information Gain)概念解释

1、 信息熵：H(X) 描述X携带的信息量。 信息量越大（值变化越多），则越不确定，越不容易被预测。

       对于抛硬币问题，每次有2种情况，信息熵为1

       对于投骰子问题，每次有6中情况，信息熵为1.75

       下面为公式：

                 

　　其中log2(p)可以理解为p这个需要用几个bit位表示。如p(x1)=1/2, p(x2)=1/4, p(x3)=1/8, p(x4)=1/8, 

      可以用x1: 1, x2: 10, x3: 110, x4: 111表示，因为为了让平均的bit位最少，概率越大的bit为设的越短。而-log2(p)正好对应bit位数。

      那么H(X)可以理解为比特位的期望值。

 

　　信息熵特点：（以概率和为1为前提哈）

　　a) 不同类别的概率分布越均匀，信息熵越大；

　　b) 类别个数越多，信息熵越大；

　　c) 信息熵越大，越不容易被预测；（变化个数多，变化之间区分小，则越不容易被预测）（对于确定性问题，信息熵为0；p=1; E=p*logp=0）

 

2、 信息增益IG(Y|X): 衡量一个属性(x)区分样本(y)的能力。 当新增一个属性(x)时，信息熵H(Y)的变化大小即为信息增益。 IG(Y|X)越大表示x越重要。

     条件熵：H(Y|X)，当X条件下Y的信息熵     

           

     信息增益： IG(Y|X)=H(Y)-H(Y|X)

熵（entropy）：在信息论和概率统计中，熵是表示随机变量不确定性的度量

条件熵（conditional entropy）：表示在一直随机变量X的条件下随机变量Y的不确定性度量。

信息增益（information gain）：信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。

信息增益比（information gain ratio）：其信息增益g(D, A)与训练数据集D关于特征A的值的熵H_A(D)之比

基尼指数（gini index）：基尼指数Gini(D)表示集合D的不确定性，基尼指数越大，样本集合的不确定性也就越大，这一点与熵相似。

2. 决策树ID3算法的思路

　　　　上面提到ID3算法就是用信息增益大小来判断当前节点应该用什么特征来构建决策树，用计算出的信息增益最大的特征来建立决策树的当前节点。这里我们举一个信息增益计算的具体的例子。比如我们有15个样本D，输出为0或者1。其中有9个输出为0， 6个输出为1。 样本中有个特征A，取值为A1，A2和A3。在取值为A1的样本的输出中，有3个输出为1， 2个输出为0，取值为A2的样本输出中,2个输出为1,3个输出为0， 在取值为A3的样本中，4个输出为1，1个输出为0.

　　　　样本D的熵为： H(D)=−(915log2915+615log2615)=0.971H(D)=−(915log2915+615log2615)=0.971

　　　　样本D在特征下的条件熵为： H(D|A)=515H(D1)+515H(D2)+515H(D3)H(D|A)=515H(D1)+515H(D2)+515H(D3)

　　　　                                                  =−515(35log235+25log225)−515(25log225+35log235)−515(45log245+15log215)=0.888=−515(35log235+25log225)−515(25log225+35log235)−515(45log245+15log215)=0.888　　　　

　　　　对应的信息增益为 I(D,A)=H(D)−H(D|A)=0.083I(D,A)=H(D)−H(D|A)=0.083　　　　　　　　　　　　

　　　　下面我们看看具体算法过程大概是怎么样的。

　　　　输入的是m个样本，样本输出集合为D，每个样本有n个离散特征，特征集合即为A，输出为决策树T。

　　　　算法的过程为：

　　　　1)初始化信息增益的阈值ϵϵ

　　　　2）判断样本是否为同一类输出DiDi，如果是则返回单节点树T。标记类别为DiDi

　　　　3) 判断特征是否为空，如果是则返回单节点树T，标记类别为样本中输出类别D实例数最多的类别。

　　　　4）计算A中的各个特征（一共n个）对输出D的信息增益，选择信息增益最大的特征AgAg

　　　　5) 如果AgAg的信息增益小于阈值ϵϵ，则返回单节点树T，标记类别为样本中输出类别D实例数最多的类别。

　　　　6）否则，按特征AgAg的不同取值AgiAgi将对应的样本输出D分成不同的类别DiDi。每个类别产生一个子节点。对应特征值为AgiAgi。返回增加了节点的数T。

　　　　7）对于所有的子节点，令D=Di,A=A−{Ag}D=Di,A=A−{Ag}递归调用2-6步，得到子树TiTi并返回。

 

3. 决策树ID3算法的不足

ID3算法虽然提出了新思路，但是还是有很多值得改进的地方。　　

　　　　a)ID3没有考虑连续特征，比如长度，密度都是连续值，无法在ID3运用。这大大限制了ID3的用途。

　　　　b)ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值的比取2个值的信息增益大。如果校正这个问题呢？

　　　　c) ID3算法对于缺失值的情况没有做考虑

　　　　d) 没有考虑过拟合的问题

　　　　ID3 算法的作者昆兰基于上述不足，对ID3算法做了改进，这就是C4.5算法，也许你会问，为什么不叫ID4，ID5之类的名字呢?那是因为决策树太火爆，他的ID3一出来，别人二次创新，很快 就占了ID4， ID5，所以他另辟蹊径，取名C4.0算法，后来的进化版为C4.5算法。下面我们就来聊下C4.5算法

4. 决策树C4.5算法的改进

　　　　上一节我们讲到ID3算法有四个主要的不足，一是不能处理连续特征，第二个就是用信息增益作为标准容易偏向于取值较多的特征，最后两个是缺失值处理的问和过拟合问题。昆兰在C4.5算法中改进了上述4个问题。

　　　　对于第一个问题，不能处理连续特征， C4.5的思路是将连续的特征离散化。比如m个样本的连续特征A有m个，从小到大排列为a1,a2,...,ama1,a2,...,am,则C4.5取相邻两样本值的中位数，一共取得m-1个划分点，其中第i个划分点Ti表示Ti表示为：Ti=ai+ai+12Ti=ai+ai+12。对于这m-1个点，分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为atat,则小于atat的值为类别1，大于atat的值为类别2，这样我们就做到了连续特征的离散化。要注意的是，与离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。

　　　　对于第二个问题，信息增益作为标准容易偏向于取值较多的特征的问题。我们引入一个信息增益比的变量IR(X,Y)IR(X,Y)，它是信息增益和特征熵的比值。表达式如下：

 

IR(D,A)=I(A,D)HA(D)IR(D,A)=I(A,D)HA(D)

 

　　　　其中D为样本特征输出的集合，A为样本特征，对于特征熵HA(D)HA(D), 表达式如下：

 

HA(D)=−∑i=1n|Di||D|log2|Di||D|HA(D)=−∑i=1n|Di||D|log2|Di||D|

 

　　　　其中n为特征A的类别数， DiDi为特征A的第i个取值对应的样本个数。D为样本个数。

　　　　特征数越多的特征对应的特征熵越大，它作为分母，可以校正信息增益容易偏向于取值较多的特征的问题。

　　　　对于第三个缺失值处理的问题，主要需要解决的是两个问题，一是在样本某些特征缺失的情况下选择划分的属性，二是选定了划分属性，对于在该属性上缺失特征的样本的处理。

　　　　对于第一个子问题，对于某一个有缺失特征值的特征A。C4.5的思路是将数据分成两部分，对每个样本设置一个权重（初始可以都为1），然后划分数据，一部分是有特征值A的数据D1，另一部分是没有特征A的数据D2. 然后对于没有缺失特征A的数据集D1来和对应的A特征的各个特征值一起计算加权重后的信息增益比，最后乘上一个系数，这个系数是无特征A缺失的样本加权后所占加权总样本的比例。

　　　　对于第二个子问题，可以将缺失特征的样本同时划分入所有的子节点，不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1，特征A有3个特征值A1,A2,A3。 3个特征值对应的无缺失A特征的样本个数为2,3,4.则a同时划分入A1，A2，A3。对应权重调节为2/9,3/9, 4/9。

 

　　　　对于第4个问题，C4.5引入了正则化系数进行初步的剪枝。具体方法这里不讨论。下篇讲CART的时候会详细讨论剪枝的思路。

　　　　除了上面的4点，C4.5和ID的思路区别不大。

　　　　

5. 决策树C4.5算法的不足与思考

　　　　C4.5虽然改进或者改善了ID3算法的几个主要的问题，仍然有优化的空间。

　　　　1)由于决策树算法非常容易过拟合，因此对于生成的决策树必须要进行剪枝。剪枝的算法有非常多，C4.5的剪枝方法有优化的空间。思路主要是两种，一种是预剪枝，即在生成决策树的时候就决定是否剪枝。另一个是后剪枝，即先生成决策树，再通过交叉验证来剪枝。后面在下篇讲CART树的时候我们会专门讲决策树的剪枝思路，主要采用的是后剪枝加上交叉验证选择最合适的决策树。

　　　　2)C4.5生成的是多叉树，即一个父节点可以有多个节点。很多时候，在计算机中二叉树模型会比多叉树运算效率高。如果采用二叉树，可以提高效率。

　　　　3)C4.5只能用于分类，如果能将决策树用于回归的话可以扩大它的使用范围。

　　　　4)C4.5由于使用了熵模型，里面有大量的耗时的对数运算,如果是连续值还有大量的排序运算。如果能够加以模型简化可以减少运算强度但又不牺牲太多准确性的话，那就更好了。

 

　　　　这4个问题在CART树里面部分加以了改进。所以目前如果不考虑集成学习话，在普通的决策树算法里，CART算法算是比较优的算法了。scikit-learn的决策树使用的也是CART算法。

对于C4.5算法，我们也提到了它的不足，比如模型是用较为复杂的熵来度量，使用了相对较为复杂的多叉树，只能处理分类不能处理回归等。对于这些问题， CART算法大部分做了改进。CART算法也就是我们下面的重点了。由于CART算法可以做回归，也可以做分类，我们分别加以介绍，先从CART分类树算法开始，重点比较和C4.5算法的不同点。接着介绍CART回归树算法，重点介绍和CART分类树的不同点。然后我们讨论CART树的建树算法和剪枝算法，最后总结决策树算法的优缺点。

1. CART分类树算法的最优特征选择方法

　　　　我们知道，在ID3算法中我们使用了信息增益来选择特征，信息增益大的优先选择。在C4.5算法中，采用了信息增益比来选择特征，以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的，这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢？有！CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的。

　　　　具体的，在分类问题中，假设有K个类别，第k个类别的概率为pkpk, 则基尼系数的表达式为：

Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kp2kGini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2

　　　　如果是二类分类问题，计算就更加简单了，如果属于第一个样本输出的概率是p，则基尼系数的表达式为：

Gini(p)=2p(1−p)Gini(p)=2p(1−p)

　　　　对于个给定的样本D,假设有K个类别, 第k个类别的数量为CkCk,则样本D的基尼系数表达式为：

Gini(D)=1−∑k=1K(|Ck||D|)2Gini(D)=1−∑k=1K(|Ck||D|)2

　　　　特别的，对于样本D,如果根据特征A的某个值a,把D分成D1和D2两部分，则在特征A的条件下，D的基尼系数表达式为：

Gini(D,A)=|D1||D|Gini(D1)+|D2||D|Gini(D2)Gini(D,A)=|D1||D|Gini(D1)+|D2||D|Gini(D2)

　　　　大家可以比较下基尼系数表达式和熵模型的表达式，二次运算是不是比对数简单很多？尤其是二类分类的计算，更加简单。但是简单归简单，和熵模型的度量方式比，基尼系数对应的误差有多大呢？对于二类分类，基尼系数和熵之半的曲线如下：

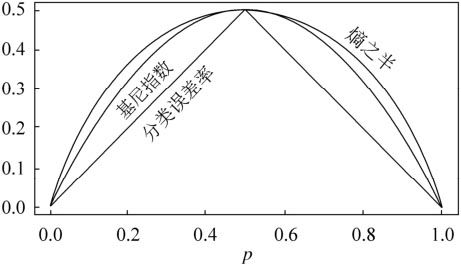
　　　　从上图可以看出，基尼系数和熵之半的曲线非常接近，仅仅在45度角附近误差稍大。因此，基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时，为了进一步简化，CART分类树算法每次仅仅对某个特征的值进行二分，而不是多分，这样CART分类树算法建立起来的是二叉树，而不是多叉树。这样一可以进一步简化基尼系数的计算，二可以建立一个更加优雅的二叉树模型。

2. CART分类树算法对于连续特征和离散特征处理的改进

　　　　对于CART分类树连续值的处理问题，其思想和C4.5是相同的，都是将连续的特征离散化。唯一的区别在于在选择划分点时的度量方式不同，C4.5使用的是信息增益，则CART分类树使用的是基尼系数。

　　　　具体的思路如下，比如m个样本的连续特征A有m个，从小到大排列为a1,a2,...,ama1,a2,...,am,则CART算法取相邻两样本值的中位数，一共取得m-1个划分点，其中第i个划分点Ti表示Ti表示为：Ti=ai+ai+12Ti=ai+ai+12。对于这m-1个点，分别计算以该点作为二元分类点时的基尼系数。选择基尼系数最小的点作为该连续特征的二元离散分类点。比如取到的基尼系数最小的点为atat,则小于atat的值为类别1，大于atat的值为类别2，这样我们就做到了连续特征的离散化。要注意的是，与离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。

　　　　对于CART分类树离散值的处理问题，采用的思路是不停的二分离散特征。

　　　　回忆下ID3或者C4.5，如果某个特征A被选取建立决策树节点，如果它有A1,A2,A3三种类别，我们会在决策树上一下建立一个三叉的节点。这样导致决策树是多叉树。但是CART分类树使用的方法不同，他采用的是不停的二分，还是这个例子，CART分类树会考虑把A分成{A1}和{A2,A3}{A1}和{A2,A3}, {A2}和{A1,A3}{A2}和{A1,A3}, {A3}和{A1,A2}{A3}和{A1,A2}三种情况，找到基尼系数最小的组合，比如{A2}和{A1,A3}{A2}和{A1,A3},然后建立二叉树节点，一个节点是A2对应的样本，另一个节点是{A1,A3}对应的节点。从描述可以看出，如果离散特征A有n个取值，则可能的组合有n(n-1)/2种。同时，由于这次没有把特征A的取值完全分开，后面我们还有机会在子节点继续选择到特征A来划分A1和A3。这和ID3或者C4.5不同，在ID3或者C4.5的一棵子树中，离散特征只会参与一次节点的建立。

3. CART分类树建立算法的具体流程

　　　　上面介绍了CART算法的一些和C4.5不同之处，下面我们看看CART分类树建立算法的具体流程，之所以加上了建立，是因为CART树算法还有独立的剪枝算法这一块，这块我们在第5节讲。

　　　　算法输入是训练集D，基尼系数的阈值，样本个数阈值。

　　　　输出是决策树T。

　　　　我们的算法从根节点开始，用训练集递归的建立CART树。

　　　　1) 对于当前节点的数据集为D，如果样本个数小于阈值或者没有特征，则返回决策子树，当前节点停止递归。

　　　　2) 计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

　　　　3) 计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和上篇的C4.5算法里描述的相同。

　　　　4) 在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2.

　　　　5) 对左右的子节点递归的调用1-4步，生成决策树。

　　　

　　　　对于生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。

4. CART回归树建立算法

　　　　CART回归树和CART分类树的建立算法大部分是类似的，所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方。

　　　　首先，我们要明白，什么是回归树，什么是分类树。两者的区别在于样本输出，如果样本输出是离散值，那么这是一颗分类树。如果果样本输出是连续值，那么那么这是一颗回归树。

　　　　除了概念的不同，CART回归树和CART分类树的建立和预测的区别主要有下面两点：

　　　　1)连续值的处理方法不同

　　　　2)决策树建立后做预测的方式不同。

　　　　对于连续值的处理，我们知道CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型，但是对于回归模型，我们使用了常见的均方差的度量方式，CART回归树的度量目标是，对于任意划分特征A，对应的任意划分点s两边划分成的数据集D1和D2，求出使D1和D2各自集合的均方差最小，同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为：

min⏟A,s[min⏟c1∑xi∈D1(A,s)(yi−c1)2+min⏟c2∑xi∈D2(A,s)(yi−c2)2]min⏟A,s[min⏟c1∑xi∈D1(A,s)(yi−c1)2+min⏟c2∑xi∈D2(A,s)(yi−c2)2]

　　　　其中，c1c1为D1数据集的样本输出均值，c2c2为D2数据集的样本输出均值。

　　　　对于决策树建立后做预测的方式，上面讲到了CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别，它采用的是用最终叶子的均值或者中位数来预测输出结果。

　　　　除了上面提到了以外，CART回归树和CART分类树的建立算法和预测没有什么区别。

5. CART树算法的剪枝

　　　　CART回归树和CART分类树的剪枝策略除了在度量损失的时候一个使用均方差，一个使用基尼系数，算法基本完全一样，这里我们一起来讲。

　　　　由于决策时算法很容易对训练集过拟合，而导致泛化能力差，为了解决这个问题，我们需要对CART树进行剪枝，即类似于线性回归的正则化，来增加决策树的返回能力。但是，有很多的剪枝方法，我们应该这么选择呢？

CART采用的办法是后剪枝法，即先生成决策树，然后产生所有可能的剪枝后的CART树，然后使用交叉验证来检验各种剪枝的效果，选择泛化能力最好的剪枝策略。

　　　　也就是说，CART树的剪枝算法可以概括为两步，第一步是从原始决策树生成各种剪枝效果的决策树，第二部是用交叉验证来检验剪枝后的预测能力，选择泛化预测能力最好的剪枝后的数作为最终的CART树。

　　　　首先我们看看剪枝的损失函数度量，在剪枝的过程中，对于任意的一刻子树T,其损失函数为：

Cα(Tt)=C(Tt)+α|Tt|Cα(Tt)=C(Tt)+α|Tt|

　　　　其中，αα为正则化参数，这和线性回归的正则化一样。C(Tt)C(Tt)为训练数据的预测误差，分类树是用基尼系数度量，回归树是均方差度量。|Tt||Tt|是子树T的叶子节点的数量。

　　　　当α=0α=0时，即没有正则化，原始的生成的CART树即为最优子树。当α=∞α=∞时，即正则化强度达到最大，此时由原始的生成的CART树的根节点组成的单节点树为最优子树。当然，这是两种极端情况。一般来说，αα越大，则剪枝剪的越厉害，生成的最优子树相比原生决策树就越偏小。对于固定的αα，一定存在使损失函数Cα(T)Cα(T)最小的唯一子树。

 

　　　　看过剪枝的损失函数度量后，我们再来看看剪枝的思路，对于位于节点t的任意一颗子树TtTt，如果没有剪枝，它的损失是

 

Cα(Tt)=C(Tt)+α|Tt|Cα(Tt)=C(Tt)+α|Tt|

 

　　　　如果将其剪掉，仅仅保留根节点，则损失是

 

Cα(T)=C(T)+αCα(T)=C(T)+α

　

 

　　　　当α=0α=0或者αα很小时，Cα(Tt)<Cα(T)Cα(Tt)<Cα(T) , 当αα增大到一定的程度时

Cα(T)=C(T)+αCα(T)=C(T)+α

。当αα继续增大时不等式反向，也就是说，如果满足下式：

 

 

α=C(T)−C(Tt)|Tt|−1α=C(T)−C(Tt)|Tt|−1

 

　　　　TtTt和TT有相同的损失函数，但是TT节点更少，因此可以对子树TtTt进行剪枝，也就是将它的子节点全部剪掉，变为一个叶子节点TT。

 

　　　　最后我们看看CART树的交叉验证策略。上面我们讲到，可以计算出每个子树是否剪枝的阈值αα，如果我们把所有的节点是否剪枝的值αα都计算出来，然后分别针对不同的αα所对应的剪枝后的最优子树做交叉验证。这样就可以选择一个最好的αα，有了这个αα，我们就可以用对应的最优子树作为最终结果。

 

　　　　好了，有了上面的思路，我们现在来看看CART树的剪枝算法。

　　　　输入是CART树建立算法得到的原始决策树TT。

　　　　输出是最优决策子树TαTα。

　　　　算法过程如下：

　　　　1）初始化αmin=∞αmin=∞， 最优子树集合ω={T}ω={T}。

　　　　2）从叶子节点开始自下而上计算各内部节点t的训练误差损失函数Cα(Tt)Cα(Tt)（回归树为均方差，分类树为基尼系数）, 叶子节点数|Tt||Tt|，以及正则化阈值α=min{C(T)−C(Tt)|Tt|−1,αmin}α=min{C(T)−C(Tt)|Tt|−1,αmin}, 更新αmin=ααmin=α

　　　　3) 得到所有节点的αα值的集合M。

　　　　4）从M中选择最大的值αkαk，自上而下的访问子树t的内部节点，如果C(T)−C(Tt)|Tt|−1≤αkC(T)−C(Tt)|Tt|−1≤αk时，进行剪枝。并决定叶节点t的值。如果是分类树，则是概率最高的类别，如果是回归树，则是所有样本输出的均值。这样得到αkαk对应的最优子树TkTk

　　　　5）最优子树集合ω=ω∪Tkω=ω∪Tk， M=M−{αk}M=M−{αk}。

　　　　6) 如果M不为空，则回到步骤4。否则就已经得到了所有的可选最优子树集合ωω.

　　　　7) 采用交叉验证在ωω选择最优子树TαTα

6. CART算法小结

　　　　上面我们对CART算法做了一个详细的介绍，CART算法相比C4.5算法的分类方法，采用了简化的二叉树模型，同时特征选择采用了近似的基尼系数来简化计算。当然CART树最大的好处是还可以做回归模型，这个C4.5没有。下表给出了ID3，C4.5和CART的一个比较总结。希望可以帮助大家理解。

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益比	支持	支持	支持
CART	分类，回归	二叉树	基尼系数，均方差	支持	支持	支持

　　　　看起来CART算法高大上，那么CART算法还有没有什么缺点呢？有！主要的缺点我认为如下：

　　　　1）应该大家有注意到，无论是ID3, C4.5还是CART,在做特征选择的时候都是选择最优的一个特征来做分类决策，但是大多数，分类决策不应该是由某一个特征决定的，而是应该由一组特征决定的。这样绝息到的决策树更加准确。这个决策树叫做多变量决策树(multi-variate decision tree)。在选择最优特征的时候，多变量决策树不是选择某一个最优特征，而是选择最优的一个特征线性组合来做决策。这个算法的代表是OC1，这里不多介绍。

　　　　2）如果样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习里面的随机森林之类的方法解决。　　　

7. 决策树算法小结

　　　　终于到了最后的总结阶段了，这里我们不再纠结于ID3, C4.5和 CART，我们来看看决策树算法作为一个大类别的分类回归算法的优缺点。这部分总结于scikit-learn的英文文档。

　　　　首先我们看看决策树算法的优点：

　　　　1）简单直观，生成的决策树很直观。

　　　　2）基本不需要预处理，不需要提前归一化，处理缺失值。

　　　　3）使用决策树预测的代价是O(log2m)O(log2m)。 m为样本数。

　　　　4）既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。

　　　　5）可以处理多维度输出的分类问题。

　　　　6）相比于神经网络之类的黑盒分类模型，决策树在逻辑上可以得到很好的解释

　　　　7）可以交叉验证的剪枝来选择模型，从而提高泛化能力。

　　　　8） 对于异常点的容错能力好，健壮性高。

　　　　我们再看看决策树算法的缺点:

　　　　1）决策树算法非常容易过拟合，导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。

　　　　2）决策树会因为样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。

　　　　3）寻找最优的决策树是一个NP难的问题，我们一般是通过启发式方法，容易陷入局部最优。可以通过集成学习之类的方法来改善。

　　　　4）有些比较复杂的关系，决策树很难学习，比如异或。这个就没有办法了，一般这种关系可以换神经网络分类方法来解决。

　　　　5）如果某些特征的样本比例过大，生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。 

　　　　性能良好的决策树的选择标准是什么？

　　　　性能良好的决策树的选择标准是一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力。言外之意就是说，好的决策树不仅对训练样本有着很好的分类效果，对于测试集也有着较低的误差率。

　　　　ID3、C4.5&CART

　　　　其实不同的决策树学习算法只是它们选择特征的依据不同，决策树的生成过程都是一样的（根据当前环境对特征进行贪婪的选择）。

　　　　ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征，每一次都选择使得信息增益最大的特征进行分裂，递归地构建决策树。

　　　　ID3算法以信息增益作为划分训练数据集的特征，有一个致命的缺点。选择取值比较多的特征往往会具有较大的信息增益，所以ID3偏向于选择取值较多的特征。

　　　　针对ID3算法的不足，C4.5算法根据信息增益比来选择特征，对这一问题进行了校正。

　　　　CART指的是分类回归树，它既可以用来分类，又可以被用来进行回归。CART用作回归树时用平方误差最小化作为选择特征的准则，用作分类树时采用基尼指数最小化原则，进行特征选择，递归地生成二叉树。

　　　　决策树的剪枝：我们知道，决策树在生成的过程中采用了贪婪的方法来选择特征，从而达到对训练数据进行更好地拟合（其实从极端角度来看，决策树对训练集的拟合可以达到零误差）。而决策树的剪枝是为了简化模型的复杂度，防止决策树的过拟合问题。具体的决策树剪枝策略可以参见李航的《统计学习方法》。

参考：http://www.cnblogs.com/maybe2030/p/4734645.html

　　   http://blog.csdn.net/ichuzhen/article/details/53981715