6.2 数据结构---树(路径)
一、路径
1.二叉树的所有路径 leetcode 257

思路:深度遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def __init__(self):
self.paths = []
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(root,path):
if not root.left and not root.right:#叶子节点
path += str(root.val)
self.paths.append(path)
return
path += str(root.val)+'->'
if root.left:
dfs(root.left,path)
if root.right:
dfs(root.right,path)
if root == None:
return []
elif not root.left and not root.right:
return [str(root.val)]
else:
dfs(root,'')
return self.paths
2.求根到叶子节点数字之和 leetcode 129


思路:深度遍历,递归保存每一条路径
这里用int(s)就可以将以0开头的字符串'00123...'转成数字,或者将很多0组成的‘000...’转成0
‘001’--> int('001')=1
'000'-->int('000')=0
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def __init__(self):
self.paths = []
def sumNumbers(self, root: TreeNode) -> int:
def dfs(root,path):
if not root.left and not root.right:#叶子
path += str(root.val)
self.paths.append(path)
return
path += str(root.val)
if root.left:
dfs(root.left,path)
if root.right:
dfs(root.right,path)
if not root:
return 0
if not root.left and not root.right:
return root.val
path = ''
dfs(root,path)
res = 0
# print(self.paths)
for i_path in self.paths:
if len(i_path) * '0' == i_path:#全0
continue
elif i_path.startswith('0'):#以0开头
while len(i_path) > 0:
if i_path.startswith('0'):
i_path = i_path[1:]
else:
print(i_path)
res += eval(i_path)
break
else:#正常
print(eval(i_path))
res += eval(i_path)
二、路径总和
1.路径总和 leetcode112
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
思路: 用栈将递归转成迭代的形式。深度优先搜索在除了最坏情况下都比广度优先搜索更快。 最坏情况是指满足目标和的 root->leaf 路径是最后被考虑的,这种情况下深度优先搜索和广度优先搜索代价是相通的。 利用深度优先策略访问每个节点,同时更新剩余的目标和。 所以我们从包含根节点的栈开始模拟,剩余目标和为 sum - root.val。 然后开始迭代:弹出当前元素,如果当前剩余目标和为 0 并且在叶子节点上返回 True; 如果剩余和不为零并且还处在非叶子节点上,将当前节点的所有孩子以及对应的剩余和压入栈中。
时间复杂度:和递归方法相同是O(N)。 空间复杂度:当树不平衡的最坏情况下是O(N) 。在最好情况(树是平衡的)下是 O(log N)。
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
if not root:
return False
de = [(root, sum - root.val), ]
while de:
node, curr_sum = de.pop()
if not node.left and not node.right and curr_sum == 0:
return True
if node.right:
de.append((node.right, curr_sum - node.right.val))
if node.left:
de.append((node.left, curr_sum - node.left.val))
return False
2.路径总和| leetcode113
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
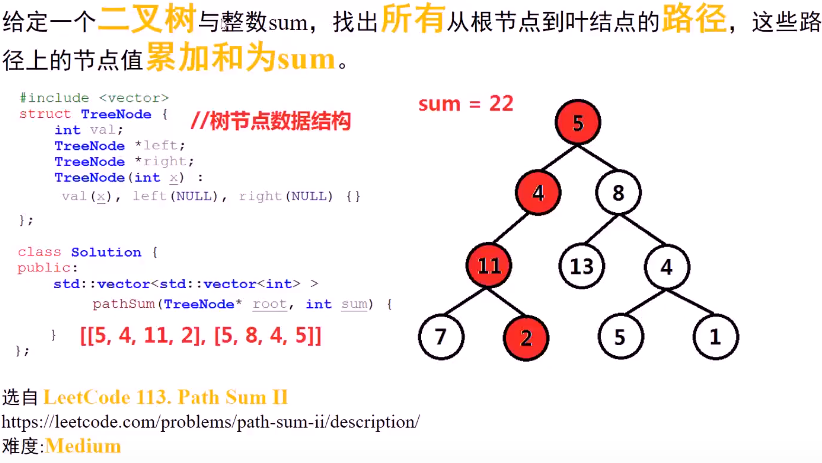
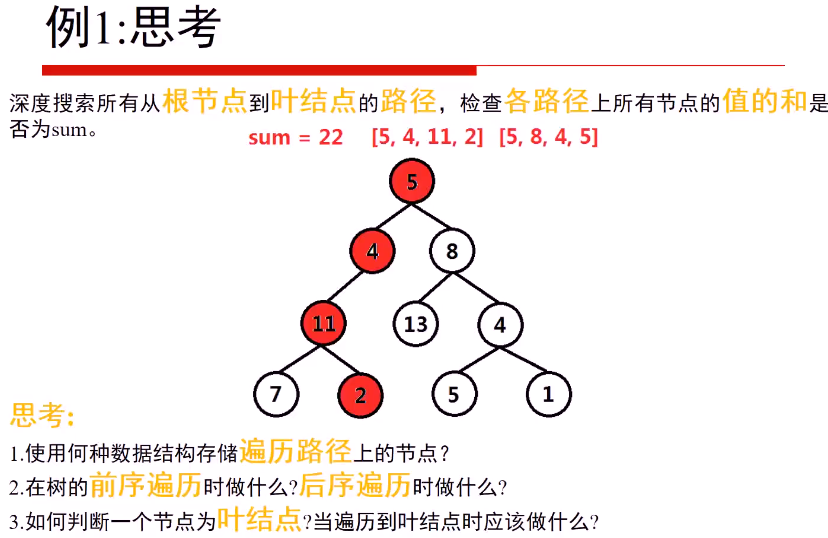
思路:
- 从根节点深度遍历二叉树,先序遍历时,将该节点值存储值path栈中,使用path_value累加节点值;
- 当遍历至叶节点时,检查path_value值是否为sum,若为sum,则将path push进入result中;
- 在后续遍历时,将该节点值从path栈中弹出,path_value减去节点值。
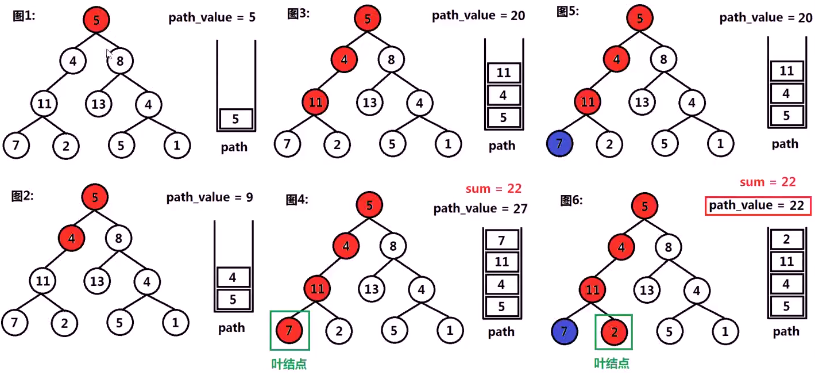


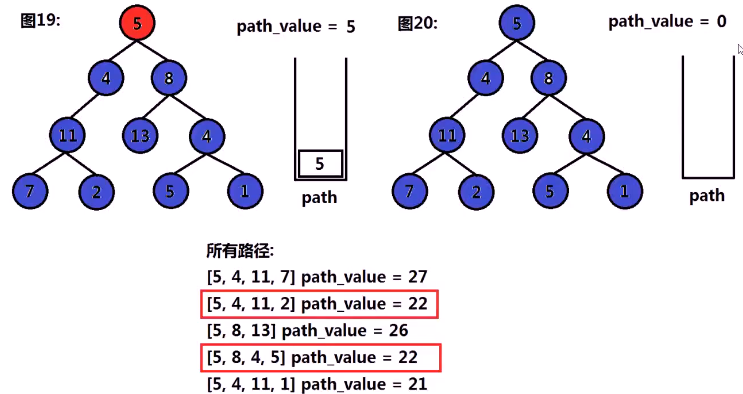
代码1:用栈
class Solution:
def pathSum2(self, root, target, ):
self.result = []
path = []
def helper(root, target, path):
if root == None:
return
path.append(root.val)
if (root.left == None) and (root.right == None) and (sum(path) == target):
tmp = path[:]
self.result.append(tmp)
helper(root.left, target, path)
helper(root.right, target, path)
path.pop()
helper(root, target, path)
return self.result
代码2:
class Solution (object):
def pathSum(self,root,sum):
"""
:type root: TreeNode
:type sum: int
:rtype: List[List[int]]
"""
res = []
if not root: return []
def helper(root, sum, tmp):
if not root:
return
if not root.left and not root.right and sum - root.val == 0:
tmp += [root.val]
res.append (tmp)
return
helper (root.left, sum - root.val, tmp + [root.val])
helper (root.right, sum - root.val, tmp + [root.val])
helper (root, sum, [])
return res
3.路径总和|| leetcode437
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
三、最大路径和
1.最大路径和 leetcode124

题目:给定一棵二叉树,求各个路径的最大和,路径可以以任意节点作为起点和终点。
思路:后序遍历,每次递归的时候只返回左子树/右子树+root.data,最大值是全局记录的,所以不需要返回
最大路径和:根据当前节点的角色,路径和可分为两种情况:
一:以当前节点为根节点
1.只有当前节点
2.当前节点+左子树🌲
3.当前节点+右子树🌲
4.当前节点+左右子树
这四种情况的最大值即为以当前节点为根的最大路径和
此最大值要和已经保存的最大值比较,得到整个树的最大路径值
二:当前节点作为父节点的一个子节点
和父节点连接的话则需取【单端的最大值】
1.只有当前节点
2.当前节点+左子树🌲
3.当前节点+右子树🌲
这三种情况的最大值
class TreeNode:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class IntRef:
def __init__(self):
self.val = None
class Solution:
def findMaxPathRecursive(self,root,maxs):
if root == None:
return 0
leftmax = self.findMaxPathRecursive(root.left,maxs)
rightmax = self.findMaxPathRecursive(root.right,maxs)
tmp = max(max(leftmax+root.data,rightmax+root.data),leftmax+rightmax+root.data)
if tmp > maxs.val:
maxs.val = tmp
print(maxs)
submax = leftmax if leftmax > rightmax else rightmax
return root.data + submax
def findMaxPath(self,root):
maxs = IntRef()
maxs.val = -2 **31
self.findMaxPathRecursive(root,maxs)
return maxs.val
if __name__ == '__main__':
root = TreeNode(2)
left = TreeNode(3)
right = TreeNode(5)
root.lef= left
root.right = right
S = Solution()
maxs = S.findMaxPath(root)
print(maxs)
四、最长同值路径
1.最长同值路径 leetcode687
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
示例1:
输入:
5
/ \
4 5
/ \ \
1 1 5
输出:2
示例 2:
输入:
1
/ \
4 5
/ \ \
4 4 5
输出:2
注意: 给定的二叉树不超过10000个结点.树的高度不超过1000。
思路:先解释一下题目,就是让我们找到一个路径,这个路径上面的值都相同,而且可以不经过根节点,例如,例2中的4-4-4这样的。 可以使用递归来做,首先,求出以每个节点为根节点的最长路径,然后从底向上,判断与父亲节点的值是否相同,如果相同,就把当前结点最长的一个分支路径加上1返回给父节点。其中,可以把最长路径保存到一个全局变量中。
class Solution (object):
def longestUnivaluePath(self, root):
"""
:type root: TreeNode
:rtype: int
"""
maxL = 0
def getMaxL(node,val):
nonlocal maxL #用来在函数或其他作用域中使用外层(非全局)变量。
if node == None:
return 0
leftMaxL = getMaxL(node.left,node.val)
rightMaxL = getMaxL(node.right,node.val)
maxL = max(maxL, leftMaxL + rightMaxL)
print('node=%s,maxL=%s'%(node.val,maxL))
if node.val == val:
return max(leftMaxL,rightMaxL) + 1
else:
return 0
if root != None:
getMaxL(root,root.val)
return maxL
def longestUnivaluePath1(self,root):
res = 0
def dns(node):
nonlocal res
if node == None:
return 0
lmax = dns(node.left)
rmax = dns(node.right)
if node.left and node.left.val == node.val:
lmax = lmax + 1
else:
lmax = 0
if node.right and node.right.val == node.val:
rmax = rmax + 1
else:
rmax = 0
res = max(res,lmax+rmax) #最大值是当前的最大值或者左右孩子路径的和。
return max(lmax,rmax) #返回值是左右路径中的最大值,因为它还需要和父节点继续构建路径。
dns(root)
return res
root = TreeNode(1)
Node1 = TreeNode(4)
Node2 = TreeNode(5)
Node3 = TreeNode(5)
Node4 = TreeNode(4)
Node5 = TreeNode(5)
Node6 = TreeNode(5)
root.left = Node1
root.right = Node2
Node1.left = Node3
Node1.right = Node4
Node2.right = Node5
Node3.left = Node5
Node5.left = Node6
S = Solution()
res = S.longestUnivaluePath1(root)
print(res)
五、公共祖先
1.找出排序二叉树上任意两个节点的公共父节点
思考:
- 两个节点的公共祖先一定在从根节点,至这两个节点的路径上;
- 由于求公共祖先中的最近公共祖先,那么即同时出现在这两条路径上的离根节点最远的节点(或离两个最近);
- 最终算法即:求p节点路径,q节点路径,两路径上最后一个相同的节点。
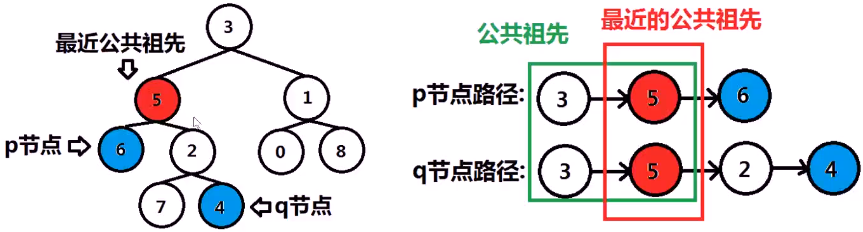
思路:先序遍历
- 从根节点遍历(搜索)至该节点,找到该节点后就结束搜索;
- 将遍历过程中遇到的节点按照顺序存储起来,这些节点即路径节点。
- 求出较短路径的长度n;
- 同时遍历p节点的路径和q节点的路径,遍历n个节点,最后一个发现的相同节点,即最近公共祖先。
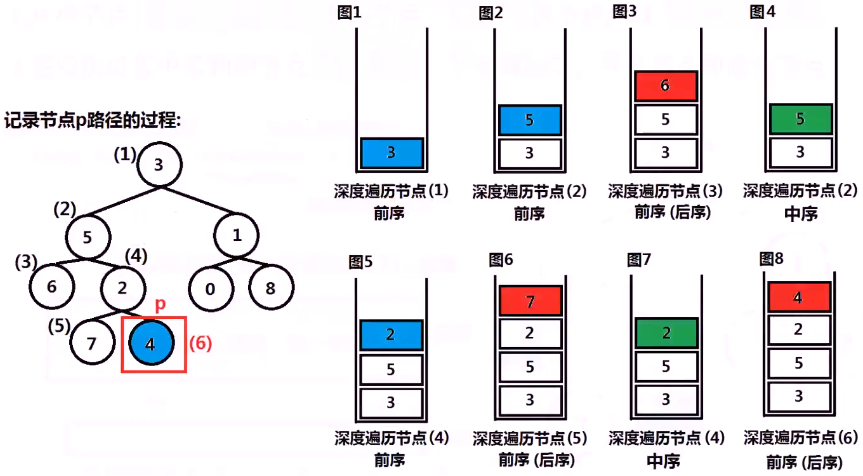
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
#获取二叉树从根节点root到node结点的路径
def getPathFromRoot(root,node,s):
'''
:param root:
:param node: 二叉树中的某个节点
:param s: 用来存储路径的栈
:return: node在root的子树上
'''
if root == None:
return False
if root == node:
s.append(root)
return root
if getPathFromRoot(root.left,node,s):
s.append(root)
return True
elif getPathFromRoot(root.right,node,s):
s.append(root)
return True
return False
#查找二叉树中两个节点最近的公共父节点
def FindParentNode(root,node1,node2):
s1 = []
path1 = getPathFromRoot(root,node1,s1)
s2 = []
path2 = getPathFromRoot(root,node2,s2)
for ss1 in s1:
print(ss1.val,end=',')
print()
for ss2 in s2:
print(ss2.val,end=',')
#找s1,s2第一个相等的节点,就是最近的公共父节点
for i in s1:
for j in s2:
if i == j:
return i.val
L1 = TreeNode(6)
L2 = TreeNode(3)
L3 = TreeNode(-7)
L4 = TreeNode(-1)
L5 = TreeNode(9)
L1.left = L2
L1.right = L3
L2.left = L4
L2.right = L5
res = FindParentNode(L1,L3,L4)
print('公共节点',res)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号