【记忆化搜索】——hdu1978—How many ways——拓扑序不明显
How many ways
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4765 Accepted Submission(s): 2818
Problem Description
这是一个简单的生存游戏,你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下:
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走,并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后,当他走到这条路径的终点时,他将只有终点所标记的能量。
![]()
如上图,机器人一开始在(1,1)点,并拥有4单位能量,蓝色方块表示他所能到达的点,如果他在这次路径选择中选择的终点是(2,4)
点,当他到达(2,4)点时将拥有1单位的能量,并开始下一次路径选择,直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数,输出的结果对10000取模。
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走,并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后,当他走到这条路径的终点时,他将只有终点所标记的能量。
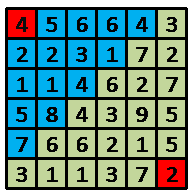
如上图,机器人一开始在(1,1)点,并拥有4单位能量,蓝色方块表示他所能到达的点,如果他在这次路径选择中选择的终点是(2,4)
点,当他到达(2,4)点时将拥有1单位的能量,并开始下一次路径选择,直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数,输出的结果对10000取模。
Input
第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。
Output
对于每一组数据输出方式总数对10000取模的结果.
Sample Input
1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2
Sample Output
3948
代码如下:
#include<iostream> #include<string.h> using namespace std; int dp[105][105];//DP[i][j]表示(i,j)到终点的方案数 int mp[105][105]; int r,c; bool inboard(int x,int y) { if(x>0&&x<=r&&y>0&&y<=c) return true; return false; } int dfs(int x,int y) { if(dp[x][y]>=0)return dp[x][y]; dp[x][y]=0; for(int i=0;i<=mp[x][y];i++) { for(int j=0;j<=mp[x][y]-i;j++) if(inboard(x+i,y+j)) { dp[x][y]=(dp[x][y]+dfs(x+i,y+j))%10000; } } return dp[x][y]; } int main() { int t; cin>>t; while(t--) { cin>>r>>c; for(int i=1;i<=r;i++) for(int j=1;j<=c;j++) cin>>mp[i][j]; //因为存在0能量点,所以0也是一种状态 //所以不能初始化为0 memset(dp,-1,sizeof(dp)); dp[r][c]=1; cout<<dfs(1,1)<<endl; } return 0; }
题后感:
白皮书上说——DP是记录中间结果再利用
那么如何寻找中间结果呢?
这道题如果用递推的思路会发现一个状态转移非常不好想,那么就利用递归——记忆化搜索
其实dfs的思路就是递归
只不过这里的递归的意义有所难理解
dfs:
终点——该点是终点 / 该点到终点的方法数已经找到
每一层递归都是由它的儿子节点决定的(有点像线段树的更新)
即:每一层既包含了该点的位置,也包含了该点的结果



 浙公网安备 33010602011771号
浙公网安备 33010602011771号