李超线段树

介绍

李超线段树是一个特别神奇的东西。TA可以把几何和线段树完美的融合起来。

题目中如果说给你一些一次函数(形如\(kx+b\))，也就是直线，或者给你一条线段(四个端点的坐标)就可以考虑用一下。

例题:洛谷P4254

题目概括:给你一些直线，同一个\(x\)坐标下\(y\)坐标的最大值。\(\color{FFFFFF}\tiny\text{众所周知，一条直线如果k>0,那TA就是单调递增的，如果k<0则是单调递减的。如果k=0,那TA平行于x轴}\)

考虑什么时候会改变最大值。

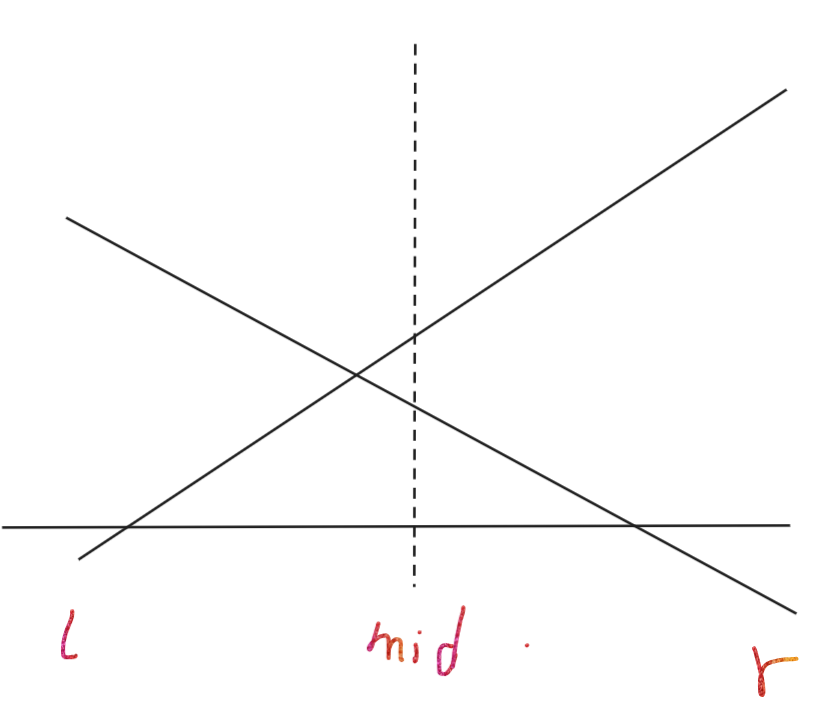
我们李超线段树存的是当前\(mid\)最大值。当\(l=r\)的时候就能查询到点了

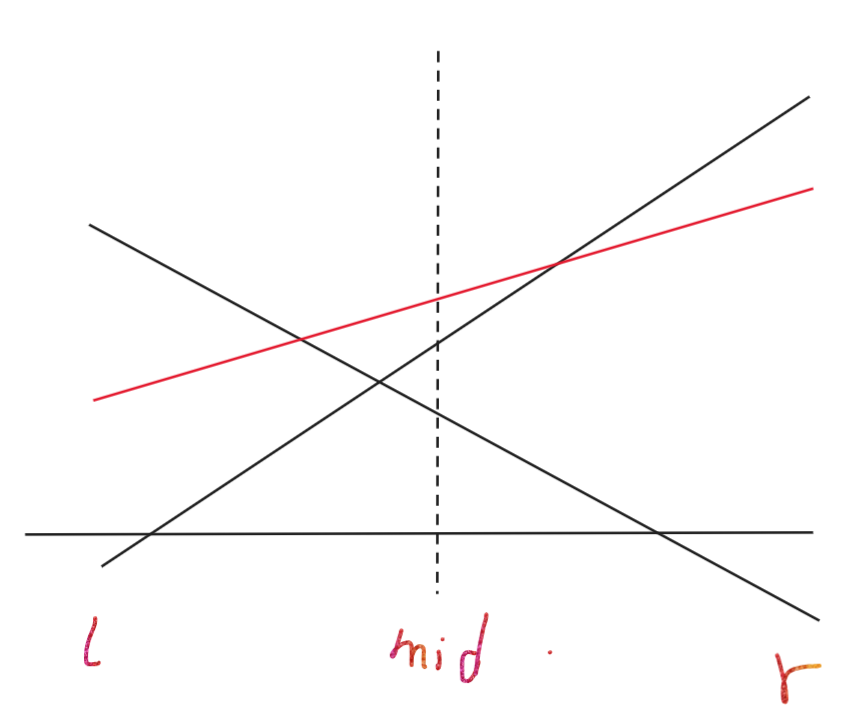
现在新插了一条直线。因为新插直线\(mid\)>以前所有\(mid\),所以肯定要把TA设为最优。但是\(l\)和\(r\)又不一定最优，所以有人就巧妙的想出来一个方法想你打不过逃课一样。

既然新线段比旧线段更好，那就让旧线段更新新线段。这就像你打瓦攻防转换一样。

为啥可以那么做，很显然。你的新线段已经是最优的了，那旧线段就不是最优的了。那肯定再更旧线段就没意义了。

所以你一个

交换一下就行了。

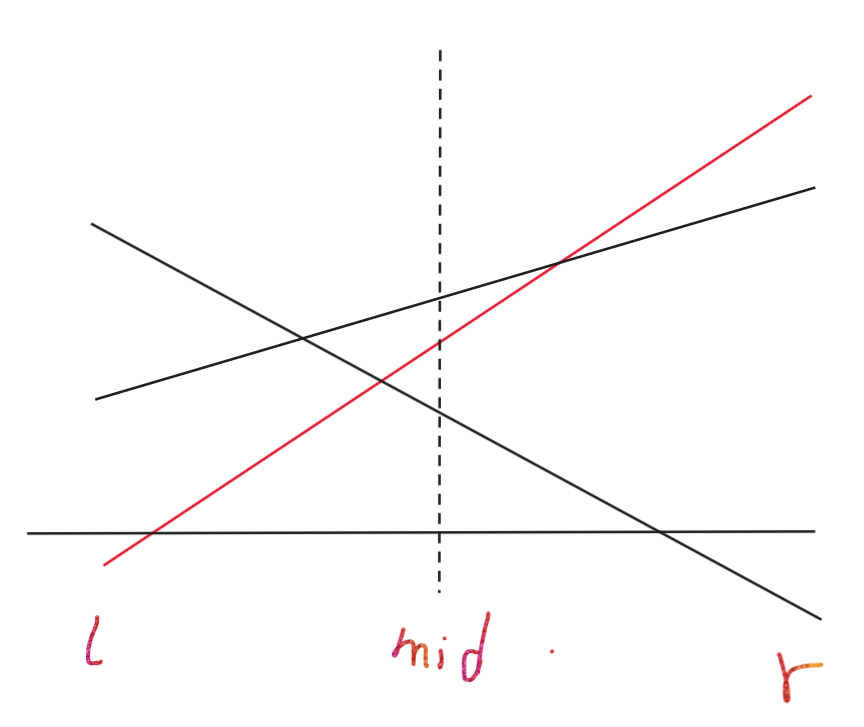
然后再比较\(l\)和\(r\)。因为你\(mid\)更优不代表你的\(l\)和\(r\)更优。

然后发现\(r\)比较大，然后就去更新左边

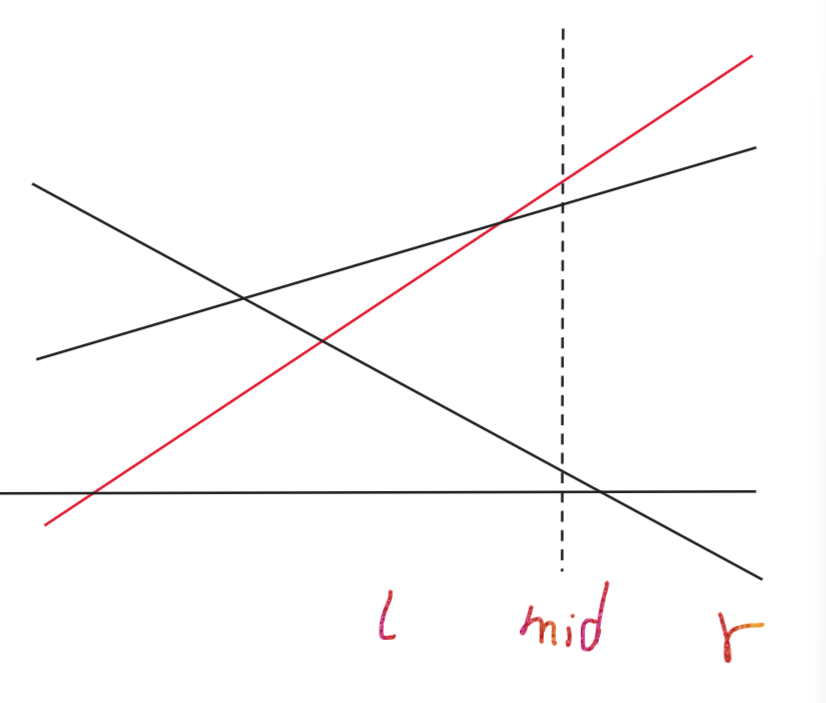
果然，现在新线段又比老线段好了。那再一个

换一下，然后一直比较就行。

时间复杂度证明

因为这两条线段时单调的，所以TA俩要么更新左边要么更新右边。那就是每次区间大小缩小\(\frac{1}{2}\),所以复杂度是\(O(n\log_2n)\)

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double lb;
const int N=5e4+10;
const int Q=1e5+10;
lb k[Q],b[Q];
ll tree[N<<2];
ll n=0;
ll ls(ll p){
	return p<<1;
}
ll rs(ll p){
	return p<<1|1;
}
lb ans(ll p,ll x)
{
	return k[p]*x+b[p];
}
void update(ll p,ll l,ll r,ll x)
{
	ll mid=l+r>>1;
	if(ans(x,mid)>ans(tree[p],mid))swap(tree[p],x);
	if(ans(x,l)>ans(tree[p],l))update(ls(p),l,mid,x);
	if(ans(x,r)>ans(tree[p],r))update(rs(p),mid+1,r,x);
}
lb query(ll p,ll l,ll r,ll x)
{
	lb res=ans(tree[p],x);
	if(l==r)return res;
	ll mid=l+r>>1;
	if(x<=mid)return max(res,query(ls(p),l,mid,x));
	else return max(res,query(rs(p),mid+1,r,x));
}
char s[8];
int main()
{
	ll q;
	scanf("%lld",&q);
	while(q--)
	{
		
		scanf("%s",&s);
		if(s[0]=='P')
		{
			n++;
			scanf("%Lf%Lf",&b[n],&k[n]);
			b[n]-=k[n]; 
			update(1,1,N,n);
		 } 
		else
		{
			ll x;
			scanf("%lld",&x);
			printf("%lld\n",max(0ll,(ll)(query(1,1,N,x))/100));
		//	printf("%Lf\n",(query(1,1,N,x)));
		}
		
	}
	return 0;
}