缩点笔记

例题

P3387 【模板】缩点
遇到这种题，你们是不是都很懵。每个点都只能经过一次，而且图里面面还有环。

法1

暴力做法都会吧。既然没规定开头，那就枚举起点，跑单源最长路。然后枚举过的打上标记。

因为\(n<m\)，所以我们用\(\mathrm{spfa}\)。算法复杂度\(O(n^2\log n)\)

法2

既然跑开头太慢了。那就每条边都走一遍。然后用上幷查集，遇到一条边就合并。但是出现了一个问题。我们无法确定来合并之后正确答案是否真对。举个例子。

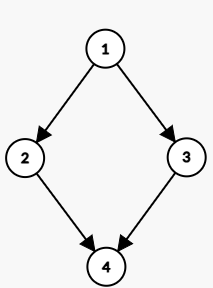
想这样的图合并之后最大值应该是四个点的权值和。但是事实上最大值是\(1\rightarrow2\rightarrow4~\mathrm{or}~1\rightarrow3\rightarrow4\)

所以这种方式是错误的。

法3

通过法2我们可以获得一些启示。并不是所有路径点权和都可以加在一起。因为中间一些点无法互相到达。如果所有点都可以互相到达，那就可一用类似于并查集的方法缩成一个点。

先来一张图

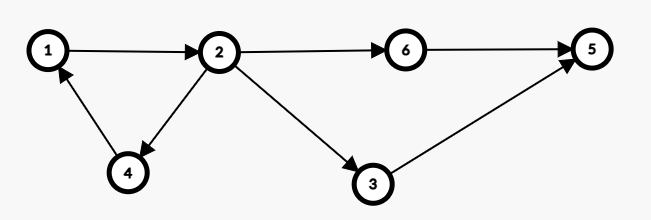
我们在里面找强联通分量。然后给强连通分量编号。

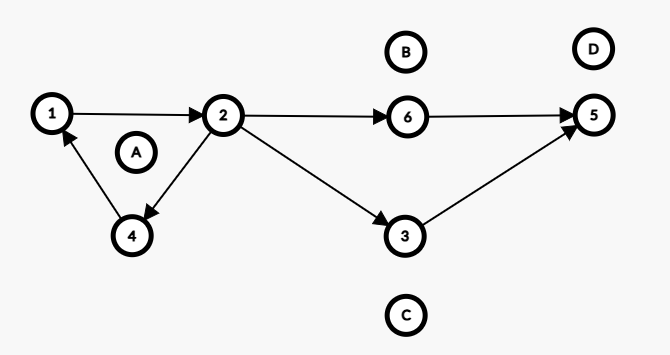
最后把原来的边移到新图上

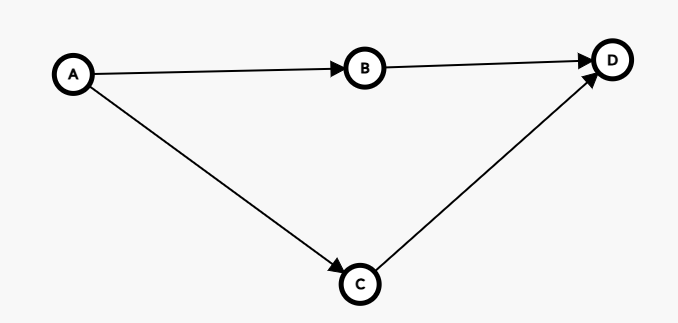
然后新图就建好了。新图的每个结点是原来的图的一个强联通分量。每条边是原来不在一个强联通分量里的点的连边。

新问题，该如何求和?其实也很简单。新点权很好求吧。就是强联通分量上的点圈之和。那我们不妨设起始的长度为当前点的点(简称\(sum_i\))。

那新边\(u\rightarrow v\)的边权就是\(sum_v\)。点有了，边也有了，那就直接跑\(\mathrm{spfa}\)就行了。

题目里没有说保证图联通，那我们需要再求强联通分量和求路径长度的时候注意一下。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
vector<int>g[N],g2[N];
int dfn[N],low[N];
int inscc[N];
bool instk[N];
int sum[N]; 
int stk[N];
int a[N];
int cnt=0,top=0,tot=0;
struct edge{
	int from,to;
}e[N];
void tarjan(int u)
{
	dfn[u]=low[u]=++cnt;
	instk[u]=1;
	stk[++top]=u;
	for(int i=0;i<g[u].size();i++)
	{
		int v=g[u][i];
		
		if(!dfn[v])
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);	
		}
		else if(instk[v])
		{
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(low[u]==dfn[u])
	{
		tot++;
		while(true)
		{

			int v=stk[top];
			instk[v]=0;
			top--;
			sum[tot]=sum[tot]+a[v];
			inscc[v]=tot;
			if(stk[top+1]==u)break;
		}
	}
}
queue<int>q;
int dis[N];
bool vis[N]; 
bool bj[N];
void spfa(int rt)
{
	q.push(rt);
	dis[rt]=sum[rt];
	while(!q.empty())
	{
		int u=q.front();
		vis[u]=0;
		q.pop();
		for(int i=0;i<g2[u].size();i++)
		{
			int v=g2[u][i];
			if(dis[v]<dis[u]+sum[v])
			{
				dis[v]=dis[u]+sum[v];
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
				}
			}
		}
	}
}
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}	
	for(int i=1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		e[i]={u,v};
		g[u].push_back(v);
	}

	for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
	for(int i=1;i<=m;i++)
	{
		int u=e[i].from,v=e[i].to;
		if(inscc[u]!=inscc[v])g2[inscc[u]].push_back(inscc[v]);
	}
	for(int i=1;i<=tot;i++)
	{
		if(!dis[i])spfa(i);
	}
	
	int mx=0;
	for(int i=1;i<=tot;i++)
	{
		mx=max(dis[i],mx);
	}
	cout<<mx;
} 

双倍经验

P3627 [APIO2009] 抢掠计划

这个题新加了两个限制:终点限制和起点限制。其实很好处理。每个新图中的点加一个变量，能不能成为终点。如果可以，那就可以作为终点取\(\max\)。

至于起点，我们知道他属于哪个强联通分量，就从哪开始。