c++凸包学习笔记

凸包简介

凸包就是把一些点的最外围那一圈的点围起来。

就像是桌上有一圈钉子，用一根橡皮筋套在最外围，然后收缩橡皮筋。形成的图形就是这一圈点的凸包。

常见的凸包算法有两种。\(\mathrm{Graham}\)算法和\(\mathrm{Andrew}\)算法。

Anderw

通过按照\(x\)坐标或\(y\)坐标从小到大排序，按照顺序来建边，加入栈中。建完看看能不能弹出上一条边。\(\mathrm{Andrew}\)算法一次能确定一个凸包的一半。

这里拿按\(x\)坐标排序，确定上凸壳

这是一张图，结点编号已按\(x\)坐标排序。

现在连接\(1,2\)结点

然后连接\(2,3\)结点。

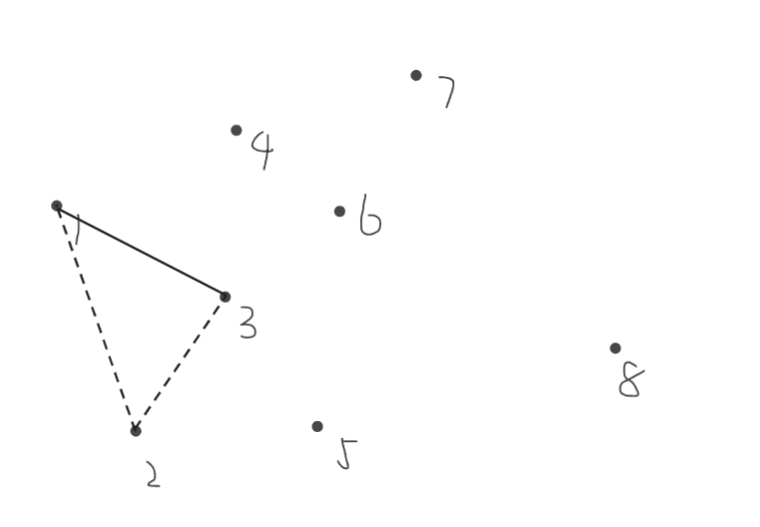
由于边\(1,3\)高于\(1,2,3\)的连边，所以可以断掉连接结点\(1,2\)的边，连接\(1,3\)。

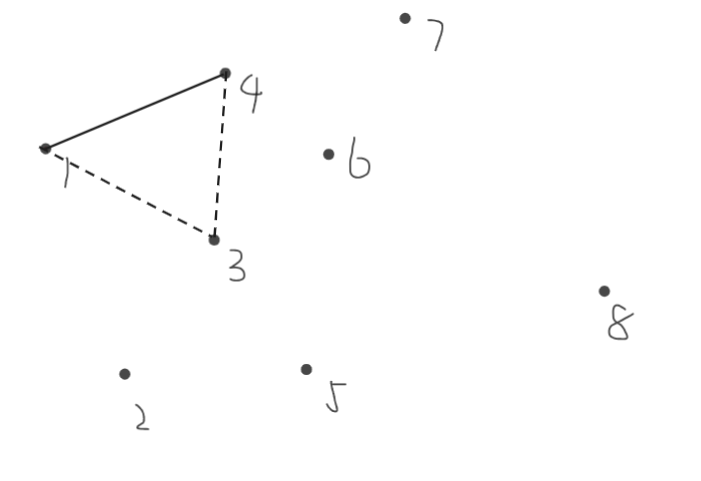
然后断掉边\(1,3\)，连接\(1,4\)。

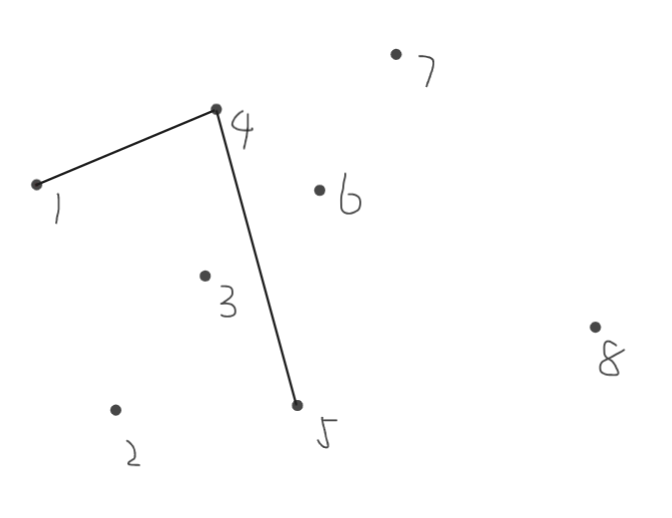
连接\(4,5\)

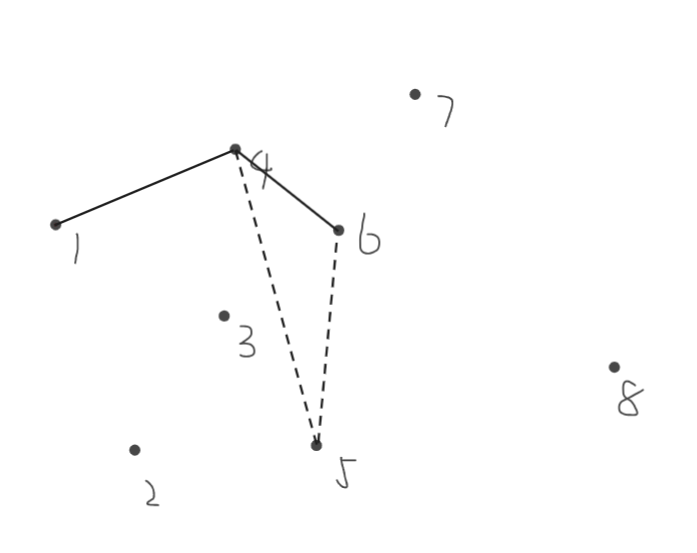
断掉边\(4,5\),连接\(4,6\)

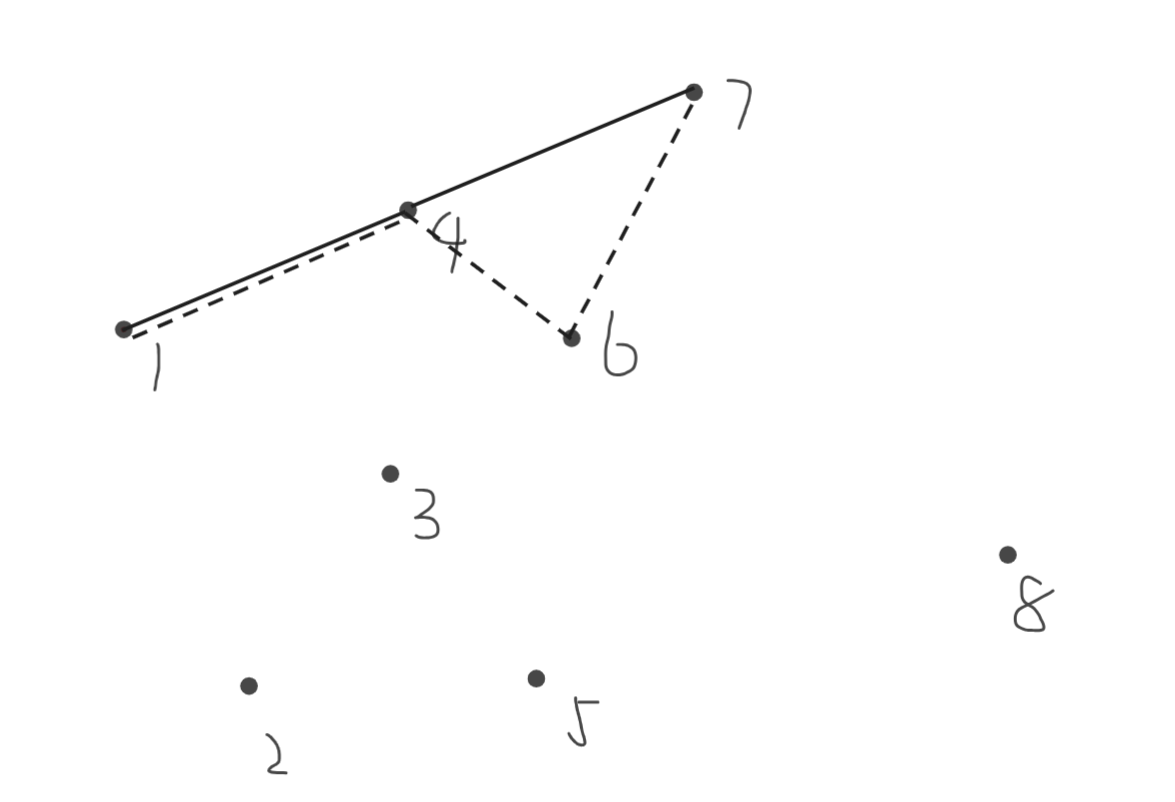
断掉边\(4,6\),连接\(4,7\)

这里发现边\(1,4\)和边\(4,7\)斜率相同，所以优先选择较远的点，这样可以让凸包中的结点变少。

所以断掉边\(1,4\),连接\(1,7\)

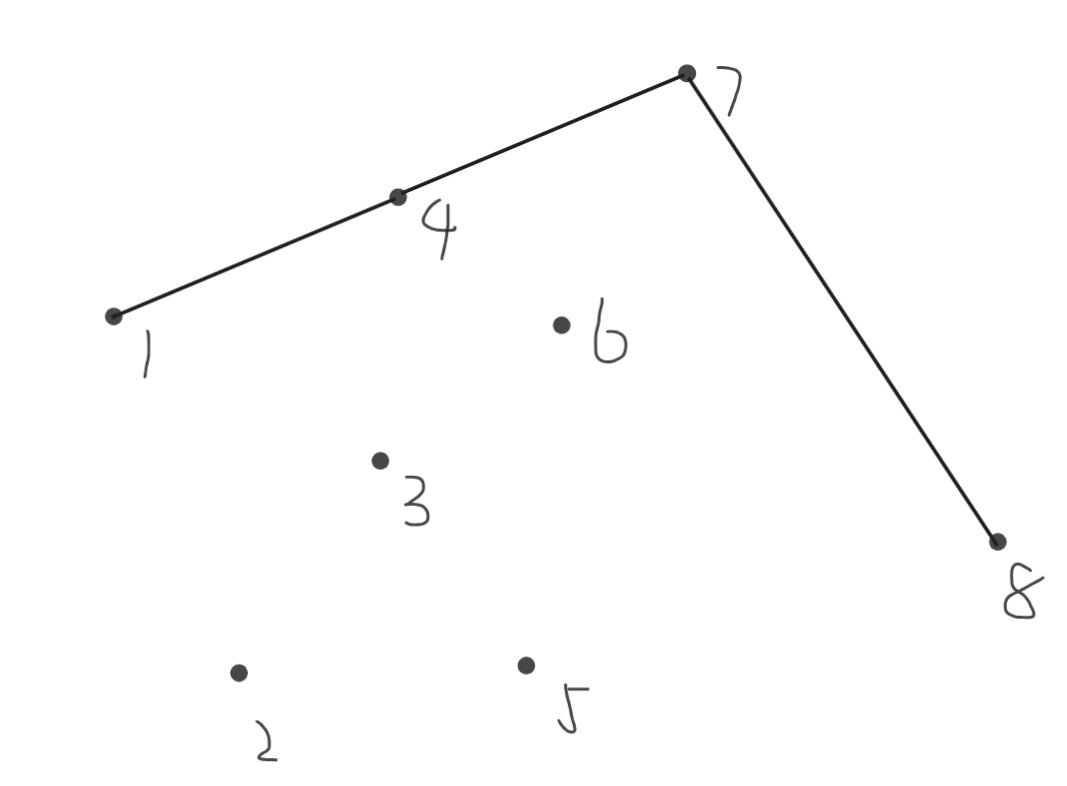
连接\(1,8\)

然后一个凸包的上凸壳也就求完了。用同样的方法可以求出下凸壳。

后两张图变大是因为我不小心把画图大小搞乱了。所以截图就那么大。

回归正题。从这里可以看出，弹点的时候可以弹多个。

要注意的是两次进行\(\mathrm{Andrew}\)的时候\(x\)坐标最小和最大的结点被记录了两次，所以只能取一次，要注意一下。

Graham

先找到一个基准点。(一般以\(x\)坐标和\(y\)坐标最小的点作为基准点。如果没有，\(x\)最小\(y\)最小都行)

然后做一条和\(x\)轴平行的直线。按照这条直线和与基准点连边形成的角度排序。再连边。

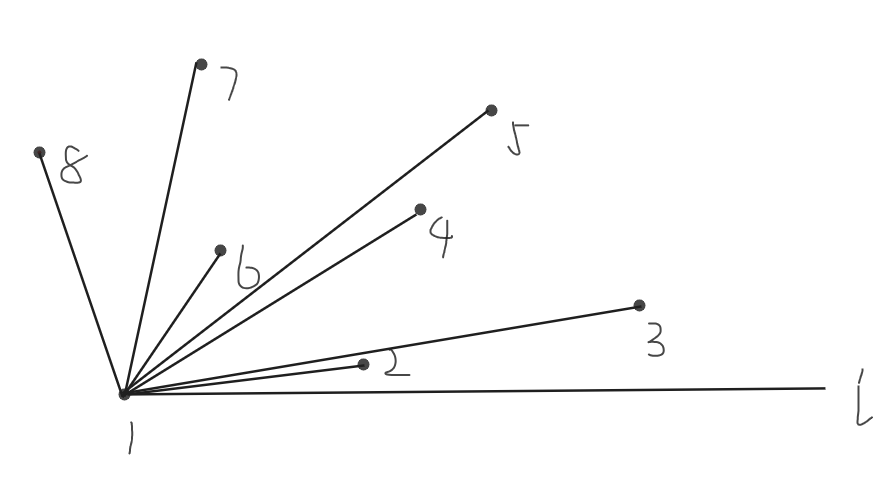
这是一张图

然后我们以\(y\)坐标最小的点为基准点，按角度排序

连接\(1,2\)

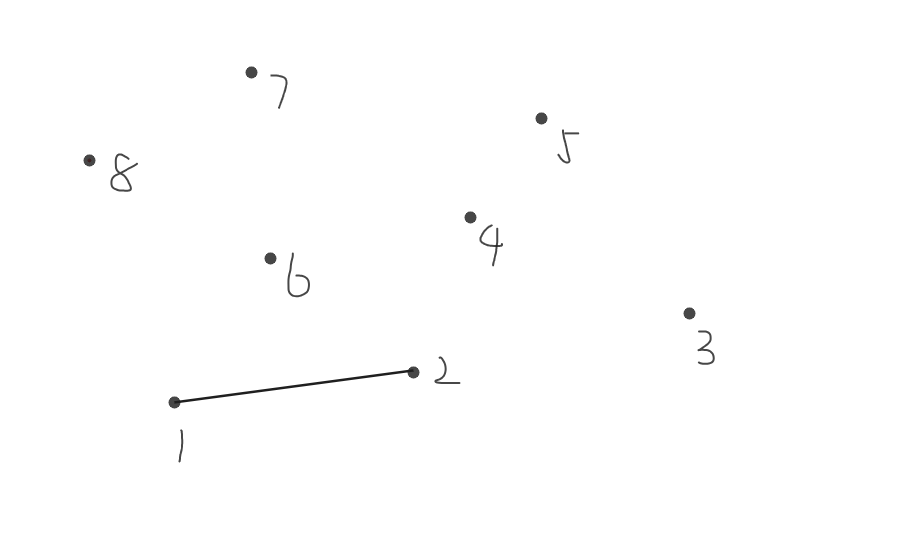
连接\(2,3\)

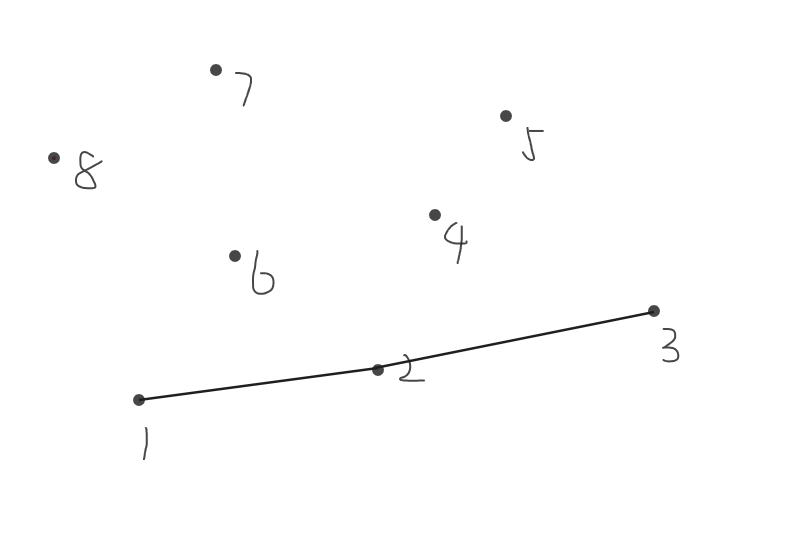
连接\(3,4\)

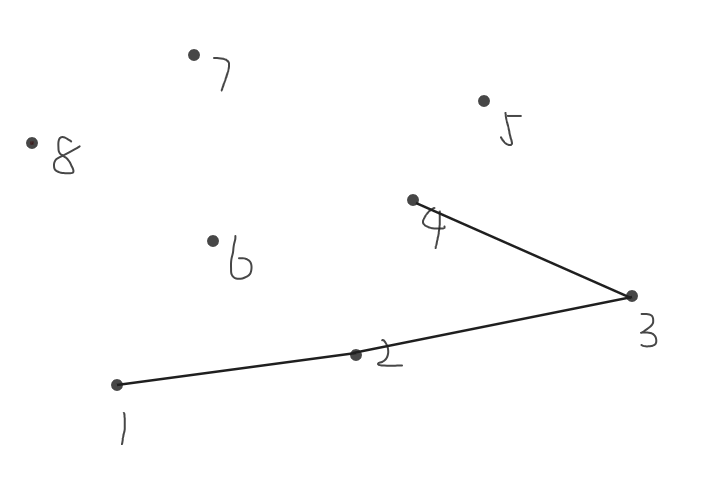
因为\(3,5\)叉积更小，所以断掉\(3,4\)，连接\(3,5\)

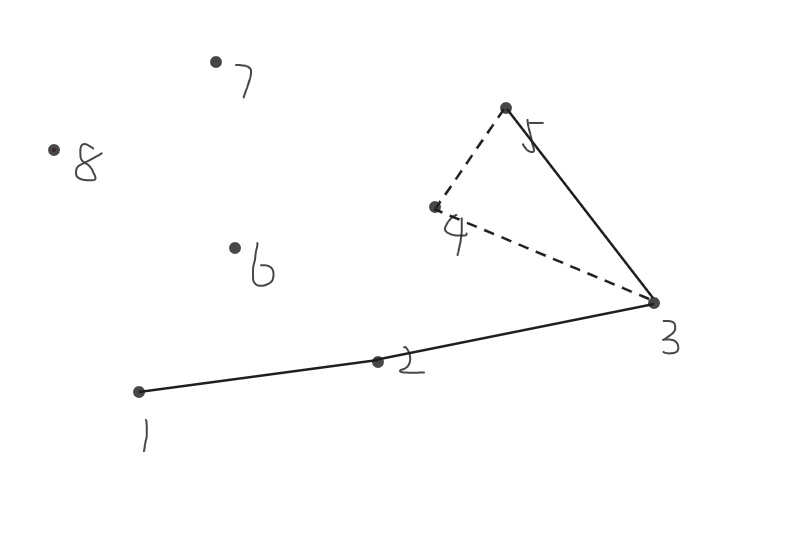
连接\(5,6\)

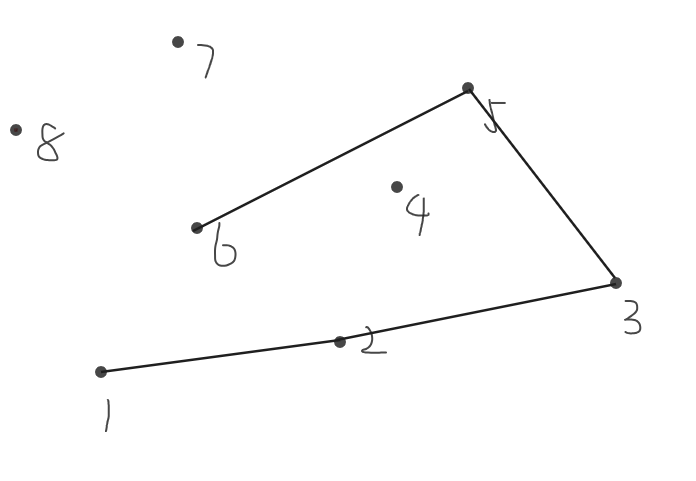
断掉\(5,6\)，连接\(5,7\)

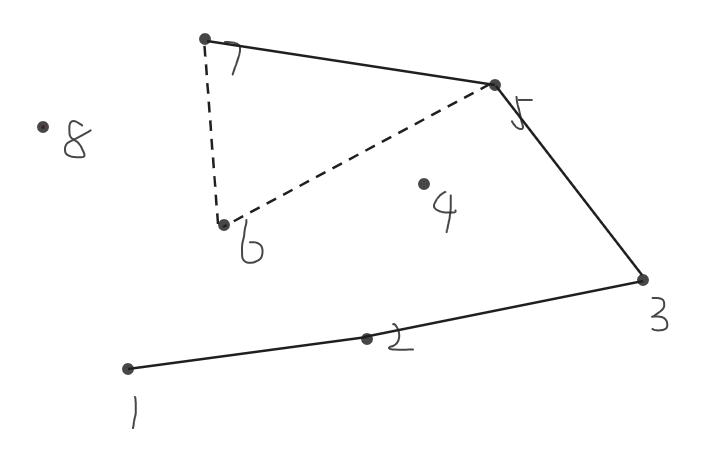
连接\(7,8\)

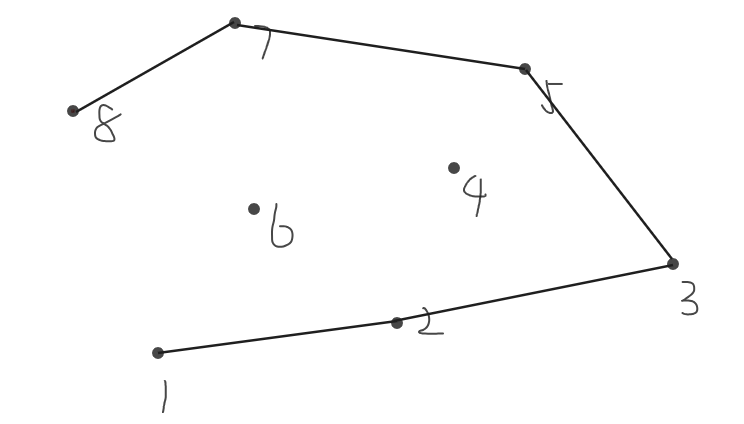
连接\(8,1\)

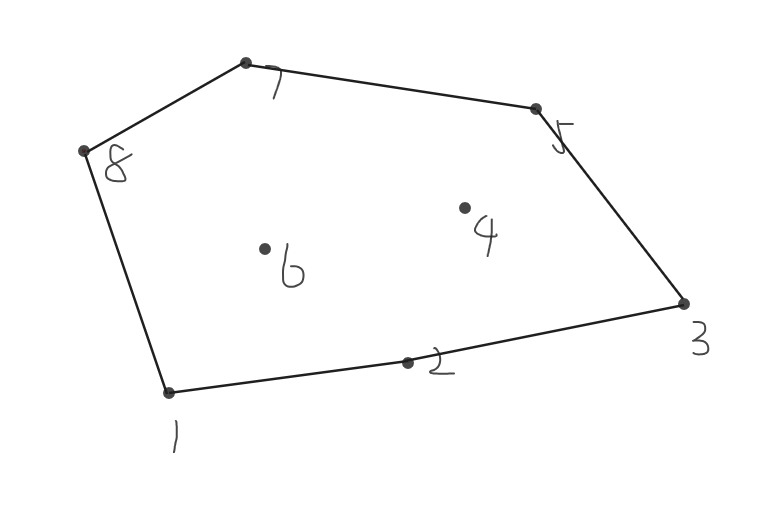
\(\mathrm{Graham}\)算法最大的区别是一次性就可以求完一整个凸包，但是这两个算法的时间复杂度是一样的。求法也类似

\(\mathrm{Graham}\)算法求到最后的时候要再连上边\(n,1\)

总之，排序是关键

例题

洛谷P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包

这个就是求凸包的周长。只要把凸包中的点存到数组里，然后可以用两点之间距离公式求出任意两点之间的距离。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node
{
	double x,y;
}a[N],s[N],s2[N];
node root;
double cross(node a,node b)//叉积    顺负逆正
{
	return a.x*b.y-a.y*b.x;
}
double check(node a1,node a2,node b1,node b2)
{
	return cross((node){a2.x-a1.x,a2.y-a1.y},(node){b2.x-b1.x,b2.y-b1.y});
}
double len(node a,node b)// 求两点距离。
{
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool cmp(node a,node b)//Graham
{
	double ck=check(root,a,root,b);
	if(ck>0)return 1;
	if(ck==0&&len((node){0,0},a)<len((node){0,0},b))//这里要把离基准点距离远的放前，这样枚举到后面就可以把前面的点弹掉
		return 1;
	return 0;
}
bool cmp2(node a,node b)//Andrew 
{
	if(a.x==b.x)return a.y<b.y;
	return a.x<b.x;
} 
int n;
void Graham()
{
	for(int i=1;i<=n;i++)//找基准点
	{
		if(i!=1&&a[i].x<a[1].x)//把想x,y最小放到最前。
		{
			swap(a[1],a[i]); 
		} 
		if(i!=1&&a[i].x==a[1].x&&a[i].y<a[1].y)
		{
			swap(a[1],a[i]); 
		}
	}
	root=a[1];//root为基准点。
	
	int top=1;
	sort(a+2,a+1+n,cmp);
	s[1]=a[1];
	for(int i=2;i<=n;i++)
	{
		while(top>1&&check(s[top-1],s[top],s[top],a[i])<=0)
			top--;
		s[++top]=a[i];
	}
	s[top+1]=a[1];//算周长，栈顶再算一遍
	double ans=0;
	for(int i=1;i<=top;i++)
	{
		ans+=len(s[i],s[i+1]);
	}
	printf("%.2Lf",ans);
}

void Andrew()
{
	sort(a+1,a+1+n,cmp2);
	int top=1;
	s[1]=a[1];
	for(int i=2;i<=n;i++)
	{
		while(top>1&&check(s[top-1],s[top],s[top],a[i])<=0)
			top--;
		s[++top]=a[i];
	}

	s2[1]=a[n];
	int top2=1;
	for(int i=n;i>=1;i--)
	{
		while(top2>1&&check(s2[top2-1],s2[top2],s2[top2],a[i])<=0)
			top2--;
		s2[++top2]=a[i];
	}
	double ans=0;	
	for(int i=1;i<top;i++)
	{
		ans+=len(s[i],s[i+1]);
	}
	for(int i=1;i<top2;i++)
	{
		ans+=len(s2[i],s2[i+1]);
	}
	printf("%.2Lf",ans);
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i].x>>a[i].y;
	}
//	Graham(); 
	Andrew();
	return 0;
}