剑指 Offer 03. 数组中重复的数字

剑指 Offer 03. 数组中重复的数字

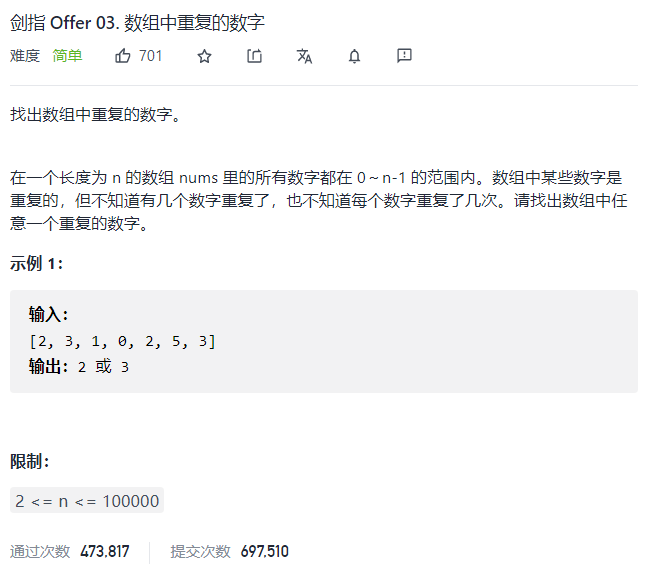
首先可以注意到数组长度为n,所有的元素都在0~n-1之间,所以可以开一个长为n的数组用来记录每个元素的次数,当某一个元素的出现频率大于2时,说明这是重复的,可以返回

class Solution {
    public int findRepeatNumber(int[] nums) {
        int n = nums.length;
        if(n == 0) {
            return 0;
        }
        // 记录0~n-1范围的数出现的频率
        int[] map = new int[n];
        for(int i = 0; i < n; i++) {
            map[nums[i]]++;
            if(map[nums[i]] > 1) {
                return nums[i];
            }
        }
        return 0;
    }
}

这里由于数据的范围可以确定在0~n-1,所以可以不用使用哈希表,因为哈希表有扩容和复制操作,时间上会更长。
时间复杂度为O(n),空间复杂度为O(n)。
还可以进行排序，如果有重复元素，那么肯定是在相邻处。

class Solution {
    public int findRepeatNumber(int[] nums) {
        int n = nums.length;
        if(n == 0) {
            return 0;
        }
        quickSort(nums, 0, n - 1);
        for(int i = 0; i < n - 1; i++) {
            if(nums[i] == nums[i + 1]) {
                return nums[i];
            }
        }
        return 0;
    }

    public void quickSort(int[] nums, int l, int r) {
        if(l >= r) return ;
        int x = nums[l + r >> 1], i = l - 1, j = r + 1;
        while(i < j) {
            do i++; while(nums[i] < x);
            do j--; while(nums[j] > x);
            if(i < j) {
                int tmp = nums[i];
                nums[i] = nums[j];
                nums[j] = tmp;
            }
        } 
        quickSort(nums, l, j);
        quickSort(nums, j + 1, r);
    }
}

快速排序的时间复杂度为O(nlogn)，空间复杂度为O(1)。
也可以使用Set来保存数组中的所有元素，尝试把nums中的每个元素都加入到Set中，如果添加失败，则说明这是一个重复元素，不能添加。

class Solution {
    public int findRepeatNumber(int[] nums) {
        Set<Integer> set = new HashSet<>(nums.length);
        for (int num : nums) {
            if (!set.add(num))
                return num;
        }
        return -1;
    }
}

时间复杂度为O(n)，空间复杂度为O(n)。
当然还有空间复杂度更低的解法，不过自己确实没有想出来，是看完了题解之后想出来的。
因为我们已经得知数的范围是在0~n-1，且对于给定的数组，索引范围也是在0~n-1，又因为有重复元素，所以肯定有索引和值的一对多关系，那么我们可以遍历所有值，以值为索引，那么有如下情况：
①.nums[i] = i，说明此数字已经放在了对应的位置，无需交换；
②.nums[nums[i]] = nums[i]，说明索引nums[i]和索引i处的值都为nums[i]，找到了一组重复的值，因此返回值nums[i]；
③.都不等时，交换索引i和nums[i]的元素值，将数字交换到对应的索引位置处，我们此时知道nums[i]的值，它放在了i处，我们需要把它放在nums[nums[i]]处，所以交换两个索引处指向的值即可。
但是这里需要注意写法，只有当nums[i] = i时，我们才递增i，否则持续交换，直到nums[i]和i不等且两个指针指向的数相同时，说明是重复元素，返回即可。

class Solution {
    public int findRepeatNumber(int[] nums) {
        int i = 0;
        while(i < nums.length) {
            //放对了自己的位置
            if(nums[i] == i) {
                i++;
                continue;
            }
            // 找到了重复元素
            if(nums[nums[i]] == nums[i]) return nums[i];
            // tmp没有放对位置,我们尝试把tmp放回它原本的位置
            int tmp = nums[i];
            nums[i] = nums[tmp];
            nums[tmp] = tmp;
        }
        return -1;
    }
}

时间复杂度为O(n)，空间复杂度为O(1)。