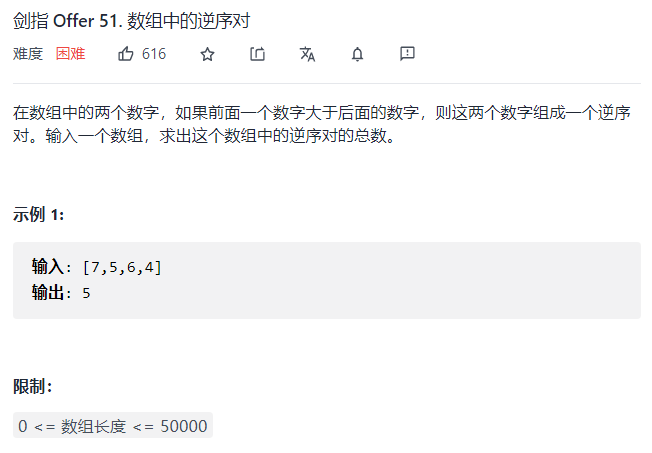
剑指 Offer 51. 数组中的逆序对

剑指 Offer 51. 数组中的逆序对

最容易想到的做法当然是暴力的枚举每一组数对，$(nums[i], nums[j])$，时间复杂度为$O(n^2)$，对应数据范围为$5e4$，很容易就超时了。

int reversePairs(int* nums, int numsSize){
    int i=0, j=0, sum=0;
    for( i=0; i<numsSize; i++ ){
        for( j=i+1; j<numsSize; j++ ){
            if( nums[j] < nums[i] ) sum++;
        }
    }
    return sum;
}

又想到是否可以利用插入排序，对于每个$nums[j]$，往前找到它的插入位置，观察其的移动次数即为逆序对数量，但是很明显插入排序的时间复杂度为$O(n^2)$，还是会超时。
所以就需要想到归并排序，在合并的过程中，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，又因为左右子数组皆有序，意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」 。
结果加上这一段的长度即为逆序对个数。