剑指 Offer 14- I. 剪绳子

剑指 Offer 14- I. 剪绳子

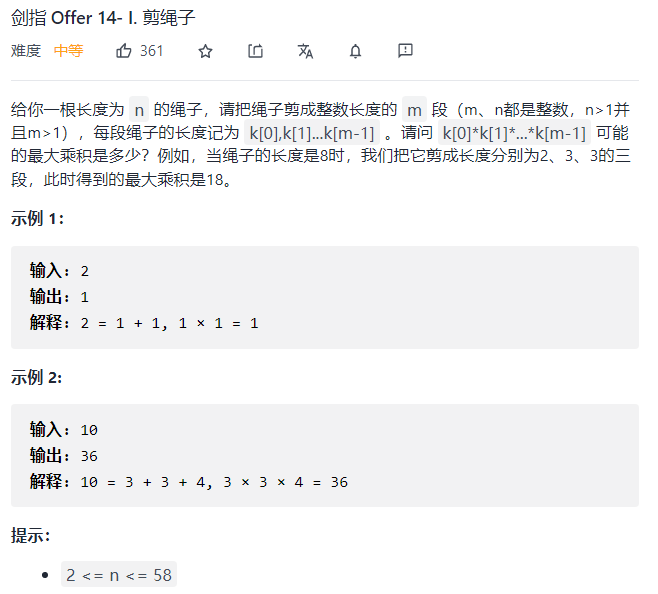
这里没有马上想到数学的方法，而是先想到了dp的方法。
对于一个整数\(i\)，如果可以被划分为\(j\)和\(i - j\)，那么设\(dp[i]\)为整数\(i\)的最大划分，则可以枚举\(1\)到\(i\)之间的所有\(j\)，\(dp[i] = Math.max(dp[i], j * (i - j)]);\)
如果一个是被拆分为多个整数，则\(dp[i] = Math.max(dp[i], j * dp[i - j]);\)。
合并起来就是\(dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));\)
故而代码如下所示:

class Solution {
    public int cuttingRope(int n) {
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for(int i = 3; i <= n; i++) {
            for(int j = 1; j < i; j++) {
                dp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));
            }
        }
        return dp[n];
    }
}

时间复杂度为\(o(n^2)\)，空间复杂度为\(O(n)\)。
因为是做剑指Offer，这里就多思考一些东西，如何再降低时间复杂度。
以下是本题中新学的东西：
1.任何大于\(3\)的数字可以被拆分为若干个\(2\)和\(3\)。
2.拆成\(2\)和\(3\)得到的乘积比直接拆得到的乘积更大，举例\(5 \Rightarrow\ (1\ +\ 4)\ or\ (2\ +\ 3)\)，且\(2 \times 3 \gt 1 \times 4\)。
3.3的个数越多，得到的结果越大。

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) {
            return n - 1;
        }
        int res = 1;
        // 这里是为了得到尽可能多的3
        while(n > 4) {
            res *= 3;
            n -= 3;
        }
        return res * n;
    }
}

时间复杂度为\(O(n)\)，空间复杂度为\(O(1)\)。