剑指 Offer 66. 构建乘积数组

剑指 Offer 66. 构建乘积数组

看到数据范围是\(1e5\)就大概猜到了不能暴力，尝试了一下也确实TLE了。

class Solution {
    public int[] constructArr(int[] a) {
        int n = a.length;
        int[] res = new int[n];
        for(int i = 0; i < n; i++) {
            int tmp = 1;
            for(int j = 0; j < n; j++) {
                if(j != i) {
                    tmp *= a[j];
                }
            }
            res[i] = tmp;
        }
        return res;
    }
}

时间复杂度为\(O(n^2)\)，空间复杂度为\(O(1)\)。

这个数据加强得有点强，以前超宽度太多了😂。
那么就肯定需要尝试新的解法，这里需要参考前缀和，\(preSum[i] = preSum[i - 1] + nums[i - 1]\)。
这里因为是乘法，我们将\(b[i]\)拆分，\(a[0] \times a[1] \times1 a[2] \times ... \times a[n - 2] \times a[n - 1]\)。
因此拆分为左半部分和右半部分。

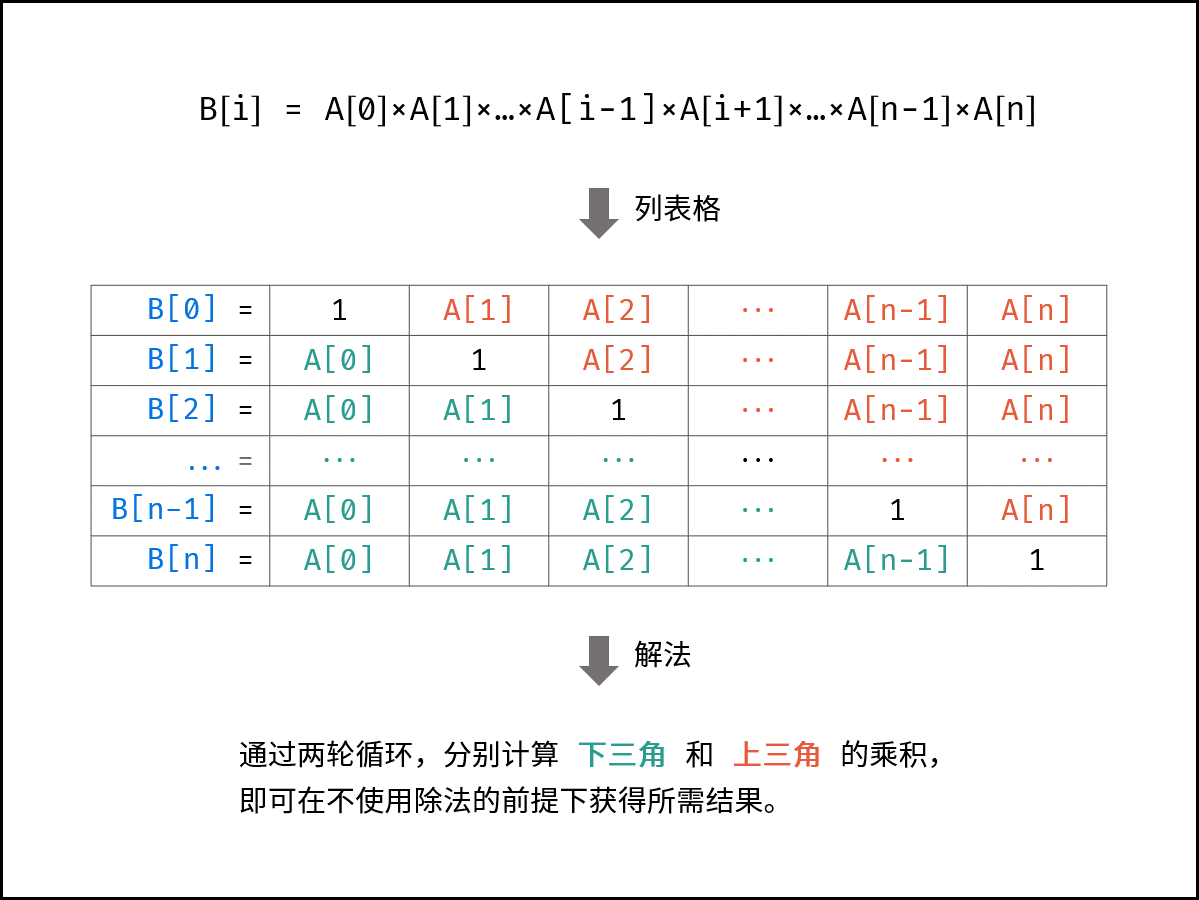
这里借用一个大佬的图。

class Solution {
    public int[] constructArr(int[] a) {
        int n = a.length;
        // left[i]表示i左侧所有元素的乘积,right[i]表示i右侧的所有元素的乘积
        int[] res = new int[n], left = new int[n], right = new int[n];
        Arrays.fill(left, 1);
        Arrays.fill(right, 1);
        // 左半部分乘积 
        for(int i = 1; i < n; i++) {
            left[i] = left[i - 1] * a[i - 1];
        }
        // 右半部分乘积
        for(int i = n - 2; i >= 0; i--) {
            right[i] = right[i + 1] * a[i + 1];
        }
        for(int i = 0; i < n; i++) {
            res[i] = left[i] * right[i];
        }
        return res;
    }
}

时间复杂度为\(O(n)\)，空间复杂度为\(O(1)\)，属于是时间换空间的典型例子，这里也可以前后分别遍历一躺，可以降低空间复杂度。