剑指 Offer 15. 二进制中1的个数

剑指 Offer 15. 二进制中1的个数

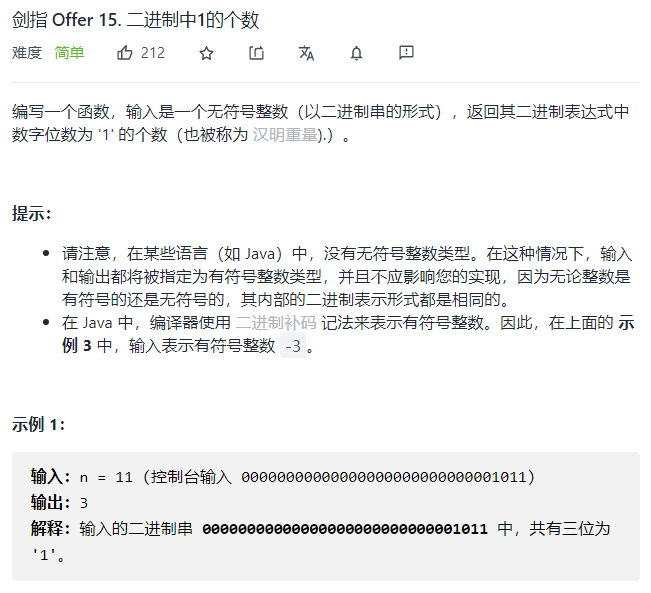
因为题目限定了是\(32\)位整数，故而我们可以枚举\(n\)的每一位即可。
\((1 << i)\)表示\(n\)的二进制数中的第\(i + 1\)位，因此我们枚举即可。

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res = 0;
        for(int i = 0; i < 32; i++) {
            if((n & (1 << i)) != 0) {
                res++;
            }
        }
        return res;
    }
}

时间复杂度\(O(32) = O(1)\)，空间复杂度\(O(1)\)。
或是从Java调接口

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        return Integer.bitCount(n);
    }
}

看了一眼源码，属实看不太明白，好像是基于分治的原理😂。
还有就是可以利用位运算中常常用到的两个性质
①.\(n \& (n - 1)\)可以消掉n最右侧的那个1；
②.\(n \& (-n)\)可以得到最右侧的1，其余全为0的数；
我们可以先用第一个结论：

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res = 0;
        while(n != 0) {
            // 这一步是为了消去最右侧的那个1
            n &= (n - 1);
            res++;
        }
        return res;
    }
}

再用第二个结论的解法

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res = 0;
        while(n != 0) {
            int rightVal = n & -n;
            n -= rightVal;
            res++;
        }
        return res;
    }
}