剑指 Offer 42. 连续子数组的最大和

剑指 Offer 42. 连续子数组的最大和

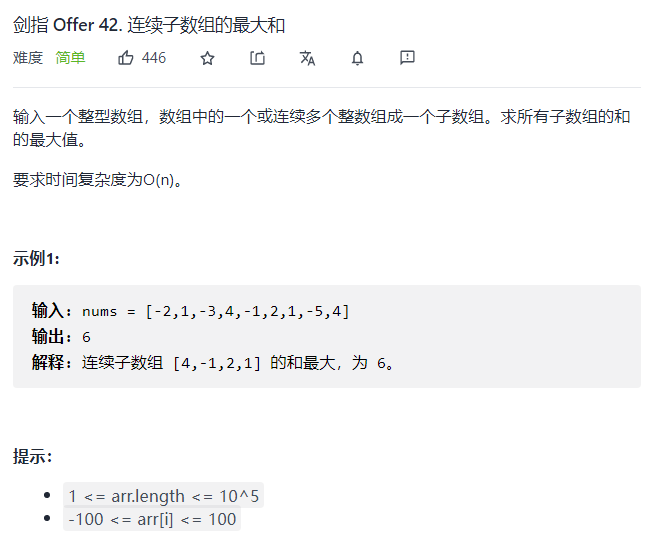
注意这里有要求要是\(O(n)\)的复杂度,我们记录dp[i]为以nums[i]结尾的最大连续子数组的和，终止返回值为ans，那么对于每一个位置i，以它结尾的子数组可以拼接前面的组成或者单独成子数组。
显然就有状态转移方程dp[i] = Math.max(dp[i - 1] + nums[i], nums[i])，同样，需要在这个过程中始终维护这个最值，ans = Math.max(ans, dp[i])。

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        if(n == 0) return 0;
        if(n == 1) return nums[0];
        // 意为以nums[i]结尾的连续子数组的最大和
        int[] dp = new int[n];
        dp[0] = nums[0];
        int ans = dp[0];
        for(int i = 1; i < n; i++) {
            dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

也看到了有前缀和做法，因为要求的是子数组，那么对于一段区间\([l, r]\)的和，就容易得到sum = preSum[r] - preSum[l]。
我们要得到最大的sum，就需要使得preSum[l]尽可能小，故而同样维护最小的preSum[l]，维护以此得到的最大和。

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        if(n == 0) return 0;
        if(n == 1) return nums[0];
        // 意为到前缀和
        int preSum = 0;
        int minPre = 0;
        int ans = Integer.MIN_VALUE;
        for(int num : nums) {
            preSum += num;
            ans = Math.max(ans, preSum - minPre);
            minPre = Math.min(minPre, preSum);
        }
        return ans;
    }
}