剑指 Offer 04. 二维数组中的查找

剑指 Offer 04. 二维数组中的查找

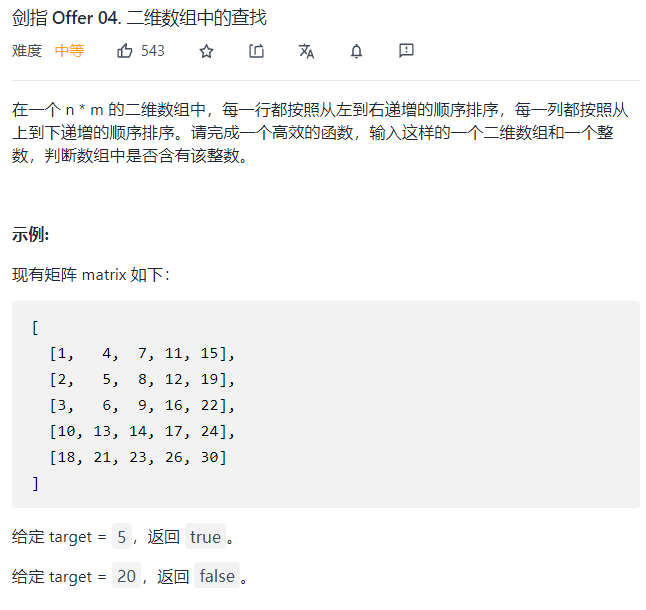
一个比较简单的办法就是直接遍历这个二维数组，但是这样的办法效率比较低，并没有用到题目中提到的行列都是递增的条件。

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        int n = matrix.length;
        if(n == 0) {
            return false;
        }
        int m = matrix[0].length;
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                if(matrix[i][j] == target) {
                    return true;
                }
            }
        }
        return false;
    }
}

上述算法的时间复杂度为\(O(m \times n)\)，空间复杂度为\(O(1)\)。
下面我们考虑如何用到给定的有序条件，可以想出，对我们需要找到一个能够让我们二分的位置，再考虑如何将二维数组扁平化。
可以看出，对于每一行至其右上角再至右下角，是一个递增的一维数组，故而考虑，对于每个右上角的顶点二分，若比要找的target更大，往左边找，即y左移，若比要找的x更小，则往更大的地方寻找，即x下移。直到索引越界为止。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int i = 0, j = n - 1;
        while(i < m && n >= 0) {
            if(matrix[i][j] == target) {
                return true;
            }else if (matrix[i][j] > target) {
                j--;
            }else {
                i++;
            }
        }
        return false;
    }
}

时间复杂度为\(O(m + n)\)，空间复杂度为\(O(1)\)。