QuickSort

QuickSort

1.综述

​ 快速排序的思想和归并排序有一点类似，都是采用分治的思想，区别在于快速排序的关键在于 pivot 将整个序列区分成为比他大\比他小的两部分，而归并则是把序列分成了两个有序的序列。

​ 快速排序的核心可以归结为以下几句话：

• 选择一个点作为 pivot(一般是最左边的点)
• 比 pivot 大的移动到右边，构成右序列；比 pivot 小的移动到左边，构成左序列
• 分别重新对左序列和右序列进行排序

2.代码

#include<iostream>
using namespace std;
//the result is an index
int extendLargeRegion(int* item,int pivot,const int &lowVac,int& high) {
	//lowVac is the position to be filled on the left
	for (int i = high ; i>lowVac; --i)
		if (item[i] < pivot) {
			item[lowVac] = item[i];
			return i;
		}
	return lowVac;
}
int extendSmallRegion(int* item, int pivot, int low, int highVac) {
	for (int i = low; i <highVac; ++i)
		if (item[i] > pivot) {
			item[highVac] = item[i];
			return i;
		}
	return highVac;
}

//attention,end is not accessible,pivot is a value not an index
int partition(int *item,int pivot,int start,int end) {
	int low = start, high = end-1;
	// low  always points to the position to be filled,so it's the return value
	while (low < high) {
		int highVac = extendLargeRegion(item, pivot, low, high);
		int lowVac = extendSmallRegion(item, pivot, low + 1, highVac);
		low = lowVac, high = highVac - 1;//highVac has been filled
	}
	return low;//which is the splitpoint
}

void quicksort(int item[],int start,int end) {
	if (start < end) {
		int pivot = item[start];
		//now we want pivot's left is less than item[pivot]
		//and the start is vacancy
		int splitPoint = partition(item, pivot, start, end);
		item[splitPoint] = pivot;
		//we don't have to handle the splitpoint
		//attention which is not accessible and which is to decide the boundary
		quicksort(item, start, splitPoint);
		quicksort(item, splitPoint + 1, end);
	}
	return;
}


int main() {
	int arr[] = { 6,4,3,5,7,9,10,14,13,12,11,18,6 };
	int capcity = sizeof(arr) / sizeof(arr[0]);
	quicksort(arr, 0, capcity);
	for (int i = 0; i < capcity; ++i)
		cout << arr[i] << " ";
	cout << endl;
	system("pause");
	return 0;
}

3.备注

​ 快速排序在很多地方都是有坑的，尤其是一些边界的选择，个人的代码中所采用的分离左右子列的办法是黄宇老师书中的思想：使用左指针和右指针不断地交替进行迭代，其步骤可以通过如下图片解释：

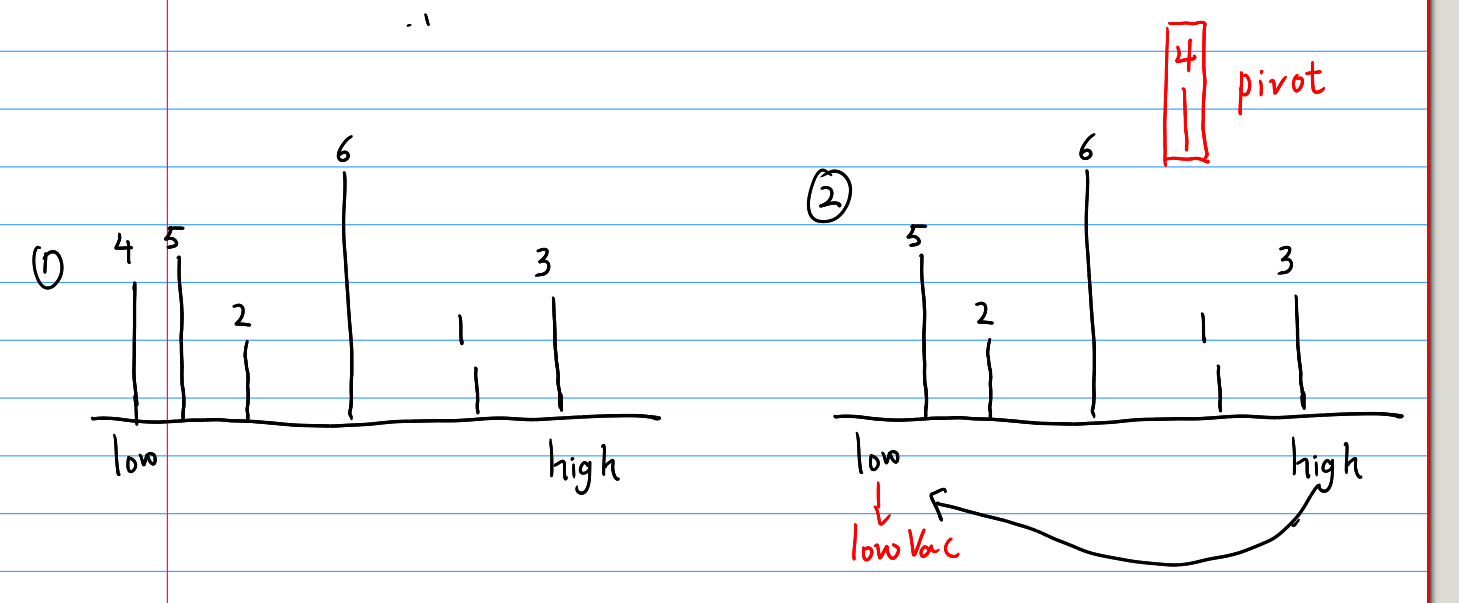
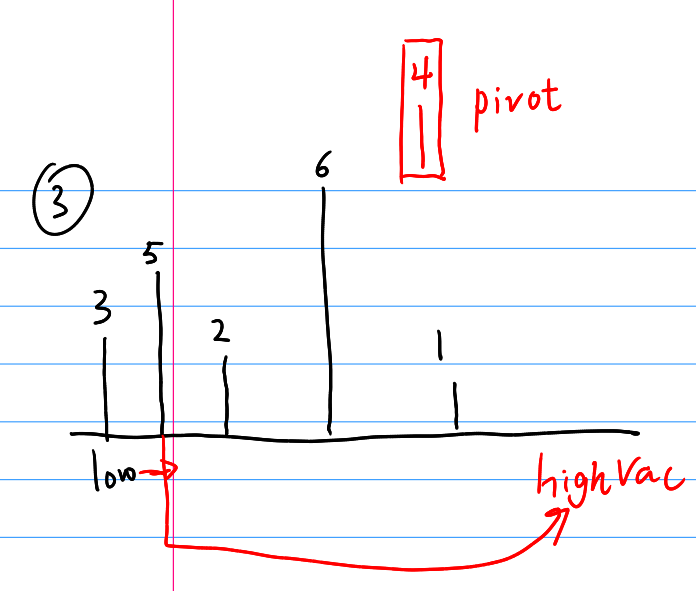
​ 这样的一个过程B站上有一个链接讲解的很好，可以参考。时间复杂度的推导很困难，会给出专门的一篇博客来进行讲解，可以强行记忆：\(Worst-case\quad O(n^2),Average\quad O(nlogn)\) 。