查全率&查准率&F_1值

查全率&查准率&F_1值

一、二分类器

​ Percision 和 Recall 两个指标存在的意义本来其实只是在二分类器中有用：有两个类别 0和1，我们预测也是0和1。这样就可以建立一个 2×2 的混淆矩阵。对于此混淆矩阵我们才可以计算查全率、查准率和F_1值。如下所示:

• 考虑 2×2 混淆矩阵

  • ACTUAL↓ \PREDICT→	POSITIVE	NEGATIVE
    TRUE	TP	FN
    FALSE	FP	TN

• 缩写的含义：

  • • TP: true positive，正确的积极预测，即预测的是积极，预测对了。
    • FN:false negative，错误的错误预测，即预测的是错误，预测错了。后略
    • FP:false positive,错误的积极预测
    • TN:true negative,正确的错误预测

• 公式;

  • \(Percision = \dfrac{TP}{TP + FP}\)
  • \(Recall = \dfrac{TP}{TP + FN}\)

• 备注：

  • 记住公式，硬套即可

    关于准确率，就不说了，上述中对角线元素和 ÷ 整个矩阵的元素和即可

二、多标签分类

​ 但是显然地，在大多数情况下，我们遇到的都不会是这样单一的双分类情况，比如在鸢尾花数据集中，我们就有着很多的类别（其实也就是三种）。在这种情况下，我们有两种办法来计算查全率和查准率。

1、micro average

​ 这个办法及其傻逼，他就是把原始公式的假正、假反搞成了其余所有的预测失败：对角线元素之外。所以整个指标就变得了傻逼了起来。因为我们会发现，这样计算的话 查全率、查准率和准确率在数值上一致

​ 我们只需要记住：micro recall = micro percision = micro accuracy即可

2、macro average

• 考虑上述公式：

  • \[Percision = \dfrac{TP}{TP + FP} \]

  • \(Recall = \dfrac{TP}{TP + FN}\)

• ​ 关于 TP的处理，没什么好说的。但是这种方法的重点就在于按行求recall，percision之后求平均值。比如对于第一行，\(T_1P_1\),显然会作为分子和分母的一部分存在。之后分别按照 one or rest 原则分别计算出来 percision 和 recall即可。再然后求平均值。

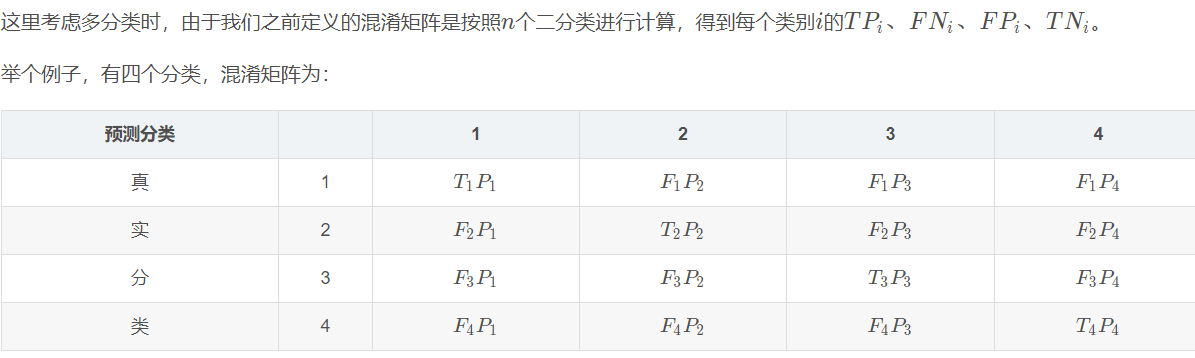
• 比如针对下面的混淆矩阵：

  • 

  • \[P_i = \dfrac{T_1 P_1}{T_1 P_1 + F_2P_1 + F_3P_1+F_4P_1}\quad{(其实就是按列)} \]

  • \[\\ R_i = \dfrac{T_1 P_1}{T_1 P_1 + F_1P_2 + F_1P_3+F_1P_4}\quad{(其实就是按行)} \]

  • 最后算平均值就好

三、F_1值

更简单了，其实就是针对上式中我们计算出 P 和 R后的调和平均数字

• 公式

• \[F\_1 = \dfrac{2}{\dfrac{1}{P} + \dfrac{1}{R}} = \dfrac{2*P*R}{P + R} \]