笔记：快速傅里叶变换（FFT）

概览

这部分介绍 FFT 可以干什么

在 OI 中，FFT 常被用来优化多项式卷积（乘法），具体原理是什么呢？

首先看看对于一个长 $n$ 的多项式 $A(x)$ 的 2 种表示法：

系数表示法

给定一个 $n$ 维向量 $a$，那么：$$A(x)=\sum_{i=0}^{n-1}a_i x^i$$

点值表示法

取 $n$ 个不同的 $x$ 值分别代入多项式，得到 $n$ 个 $A(x)$ 的结果 $y$。

即对于 $1\leq i\leq n$，有：$$y_i=A(x_i)$$

这就可以唯一确定一个多项式了，必要时可以高斯消元解出系数表示法的 $a$

注意到多项式乘法，系数表示法直接计算是 $O(n^2)$ 的；但对于点值表示法，只要 $x_i$ 统一，那么 $y_i$ 的计算是 $O(n)$ 的，很有优化空间

这时多项式乘法问题就变成了：

将 2 个多项式的系数表示法快速转成点值表示法
$O(n)$ 将两个点值表示法的 $y_i$ 相乘，得到乘积的点值表示法
将乘积的点值表示法快速转成系数表示法

瓶颈出在了 1、3 步，这就是 FFT 干的事情了

复数单位根

要想快速完成 1、3 步，代入的 $x_i$ 就必须要有足够优秀的性质

这里取单位根作为 $x_i$ 代入

复数基础

定义虚数：$i=\sqrt{-1}$

定义复数：$c=a+bi$

复数加法：$c_1+c_2=(a_1+a_2)+(b_1+b_2)i$

复数减法：$c_1-c_2=(a_1-a_2)+(b_1-b_2)i$

复数乘法：$c_1\cdot c_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i$

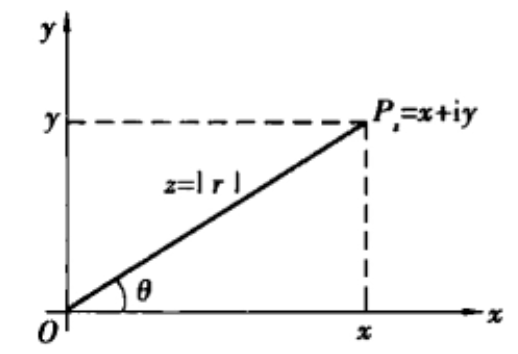
复数模长：$|c|=\sqrt{a^2+b^2}$

复数辐角：$\theta$

图来自度娘

因此一个复数 $c=|c|\cos{\theta}+i|c|\sin{\theta}$

复数乘法有一个重要性质：模长相乘，辐角相加，自己推推即可证明。

单位根

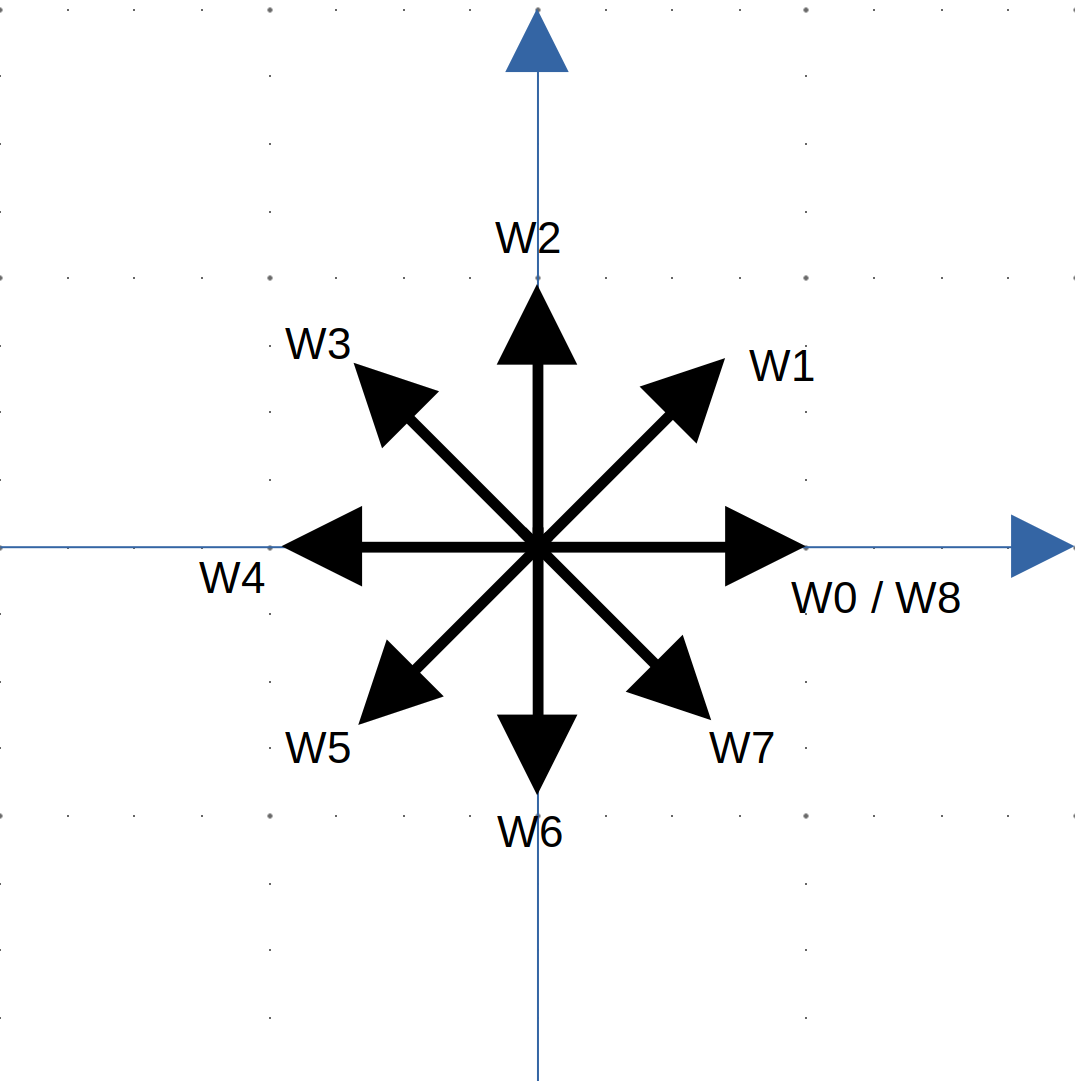
是一些特殊的模长为 1 的复数，记为：$\omega_n^k$

在 $n=8$ 时长这个样子：

图中 $Wk$ 即为 $\omega_8^k$

单位根的一些性质：

\[\omega_n^n=\omega_n^0=1 \]
\[\omega_n^k=\cos{\frac{k}{n}2\pi}+i\sin{\frac{k}{n}2\pi} \]
\[\omega_n^k=\omega_{ni}^{ki} \]

用三角函数展开易证

\[\omega_n^k=\omega_{n}^{k+n} \]

用三角函数展开易证，参考图片相当于是转了一圈又回来了

\[\omega_n^k=-\omega_n^{k+\frac{n}{2}} \]

这里 $n$ 为偶数，参考图片相当于是转了半圈，此时方向刚好相反

离散傅里叶变换（DFT）

一种龟速将多项式的系数表示法转成点值表示法的方式。
其实就是 $O(n^2)$ 暴力代单位根

前面讲过用多项式的点值表示法要代单位根有优秀性质，实际上这个过程就是 DFT。

即对于 $0\leq k< n$，有：

\[y_k=A(\omega_n^{k})=\sum_{i=0}^{n-1}a_i\cdot(\omega_n^{k})^i \]

离散傅里叶逆变换（IDFT）

一种利用单位根性质将多项式点值表示法 $O(n^2)$ 转为系数表示法的方式。
比高斯消元的 $O(n^3)$ 优秀了不少

把多项式 $A(x)$ 的离散傅里叶变换结果作为另一个多项式 $B(x)$ 的系数，取单位根的倒数，作为 $x$ 代入 $B(x)$，得到的每个数再除以 $n$，得到的就是 $A(x)$ 的各项系数，这个过程就是 IDFT。

即对于 $0\leq k< n$，有：

\[z_k=B(\omega_n^{-k})=\sum_{i=0}^{n-1}y_i\cdot (\omega_n^{-k})^i=n\cdot a_k \]

证明：$z_k=n\cdot a_k$

我们有：

\[y_k=\sum_{i=0}^{n-1}a_i\cdot\omega_n^{ik} \]
\[z_k=\sum_{i=0}^{n-1}y_i\cdot\omega_n^{-ik} \]

将 $y_i$ 代入，得：

\[z_k=\sum_{i=0}^{n-1}(\omega_{n}^{-ik}\sum_{j=0}^{n-1}a_j\cdot\omega_n^{ij}) \]

\[z_k=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^i)^{j-k} \]

\[z_k=\sum_{j=0}^{n-1}a_j\sum_{i=0}^{n-1}(\omega_n^i)^{j-k} \]

现在我们关注：

\[\sum_{i=0}^{n-1}(\omega_n^i)^{j-k} \]

注意到：当 $j=k$ 时，整个式子的值为 $n$

对于其他情况，根据等比数列求和公式，整个式子的值为：

\[\sum_{i=0}^{n-1}(\omega_n^{j-k})^i=\frac{(\omega_n^{j-k})^n-1}{\omega_n^{j-k}-1}=\frac{(\omega_{n}^n)^{j-k}-1}{\omega_n^{j-k}-1}=0 \]

所以：

\[z_k=a_k\cdot n \]

证毕。

快速傅里叶变换和逆变换（FFT）

一种对 DFT、IDFT 的优化，能快速将多项式的系数表示法转为点值表示法
时间复杂度 $O(nlogn)$

注意到 IDFT 与 DFT 有着相同的形式，我们只需要解决 DFT 即可。

分治实现

举一个 $n=8$ 的例子：

\[f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7 \]

按下标的奇偶性分开：

\[f(x)=(a_0+a_2x^2+a_4x^4+a_6x^6)+(a_1x+a_3x^3+a_5x^5+a_7x^7) \]

\[f(x)=(a_0+a_2x^2+a_4x^4+a_6x^6)+x(a_1+a_3x^2+a_5x^4+a_7x^6) \]

设：

\[g(x)=a_0+a_2x+a_4x^2+a_6x^3 \]

\[h(x)=a_1+a_3x+a_5x^2+a_7x^3 \]

则：

\[f(x)=g(x^2)+xh(x^2) \]

代入 $x=\omega_n^k$，利用前面提到的单位根的性质推一推：

\[f(\omega_n^k)=g(\omega_{\frac{n}{2}}^k)+\omega_n^kh(\omega_{\frac{n}{2}}^k) \]

\[f(\omega_n^{k+\frac{n}{2}})=g(\omega_{\frac{n}{2}}^k)-\omega_n^kh(\omega_{\frac{n}{2}}^k) \]

这里的 $n$ 为偶数，$k\leq\frac{n}{2}$

发现 $g(x)$ 和 $h(x)$ 都是与 $f(x)$ 本质相同的子问题，递归求解即可。

时间复杂度：

\[T(n)=2T(\frac{n}{2})+n \]

显然用主定理分析一下是 $O(nlogn)$ 的。

注意这里的 $n$ 必须是 2 的幂次（否则递归递归着系数没了）
多项式项数不足的话高位补 0 补到即可

void fft(cpl *f, int n, int o) // o 为 1 时是 FFT，为 -1 时是 IFFT
{
    if (n == 1)
        return;
    for (int i = 0; i < n; i += 1) t[i] = f[i];
    for (int i = 0; i < n; i += 2) f[i / 2        ] = t[i];
    for (int i = 1; i < n; i += 2) f[i / 2 + n / 2] = t[i]; // 按奇偶性分开

    cpl *g = f;
    cpl *h = f + n / 2;
    fft(g, n / 2, o); // 递归求解
    fft(h, n / 2, o);

    cpl w(1, 0);
    cpl s(cos(pi * 2 / n), sin(pi * 2 / n) * o);

    for (int k = 0; k < n / 2; k ++)
        t[k        ] = g[k] + w * h[k],
        t[k + n / 2] = g[k] - w * h[k],
        w = w * s;
    for (int i = 0; i < n; i ++) f[i] = t[i];
}

倍增实现

分治实现需要用到递归，常数较大，考虑优化。

继续用 $n=8$ 举例子，我们来观察一下分治实现的每次层会把系数怎么排序：

\[a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7 \]

\[a_0,a_2,a_4,a_6|a_1,a_3,a_5,a_7 \]

\[a_0,a_4|a_2,a_6|a_1,a_5|a_3,a_7 \]

把系数在最后一行的下标的二进制打个表：

$a$ 第一行的下标	$a$ 最后一行的下标
000	000
001	100
010	010
011	110
100	001
101	101
110	011
111	111

考虑每次把奇偶项分开就是对系数下标的二进制从低位到高位进行一个类似基数排序的东西，最后造成系数最终的下标与开始的下标的二进制是对称的。

下标二进制是左右对称的，
这玩意貌似叫蝶形变换？

设 $p_i$ 表示 $i$ 的最终位置，即 $i$ 与 $p_i$ 的二进制是对称的，那么显然有递推式：

p[i] = (p[i >> 1] >> 1) | ((i & 1) << l - 1);

其中 $l$ 是 $log_2n$
递推式的含义就是把最低位抹掉把最高位填上去

因此我们可以 $O(n)$ 搞出最后的位置，然后用循环的方式一层一层推上去，这样就避免了递归和回溯。

inline void fft(cpl *f, int o)
{
    for (int i = 0; i < k; i += 1) if (i < p[i]) swap(f[i], f[p[i]]); // k 相当于 n，表示总的项数
    for (int i = 1; i < k; i *= 2) // i 表示当前区间长度的一半
    {
        cpl s(cos(pi / i), sin(pi / i) * o); 
        for (int j = 0; j < k; j += i << 1) // j 表示枚举到的区间左端点
        {
            cpl w(1, 0), x, y;
            for (int t = 0; t < i; t ++, w = w * s) // t 枚举的是下标
                x = f[j + t],
                y = f[j + t + i] * w,
                f[j + t    ] = x + y,
                f[j + t + i] = x - y;
        }
    }
}

P3803 【模板】多项式乘法（FFT）

分治实现

// P3803 (AC)

#include <bits/stdc++.h>

using namespace std;

const double pi = acos(-1);

inline int read()
{
    int val = 0;
    bool si = 0;
    char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) si ^= ch == '-';
    for (;  isdigit(ch); ch = getchar())
        val = (val << 3) + (val << 1) + (ch ^ 48);
    return si == 0 ? val : -val;
}

const int N = 4e6 + 5;

int n, m, k;

struct cpl
{
    double r, i;

    cpl(double R = 0, double I = 0)
    {
        r = R;
        i = I;
    }

    friend cpl operator + (cpl a, cpl b) {return cpl(a.r + b.r, a.i + b.i); }
    friend cpl operator - (cpl a, cpl b) {return cpl(a.r - b.r, a.i - b.i); }
    friend cpl operator * (cpl a, cpl b) {return cpl(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r); }

} t[N], a[N], b[N], c[N];

void fft(cpl *f, int n, int o)
{
    if (n == 1)
        return;
    for (int i = 0; i < n; i += 1) t[i] = f[i];
    for (int i = 0; i < n; i += 2) f[i / 2        ] = t[i];
    for (int i = 1; i < n; i += 2) f[i / 2 + n / 2] = t[i];

    cpl *g = f;
    cpl *h = f + n / 2;
    fft(g, n / 2, o);
    fft(h, n / 2, o);

    cpl w(1, 0);
    cpl s(cos(pi * 2 / n), sin(pi * 2 / n) * o);

    for (int k = 0; k < n / 2; k ++)
        t[k        ] = g[k] + w * h[k],
        t[k + n / 2] = g[k] - w * h[k],
        w = w * s;
    for (int i = 0; i < n; i ++) f[i] = t[i];
}

int main()
{
    n = read() + 1;
    m = read() + 1;
    for (k = 1; k <= n + m; k <<= 1);
    for (int i = 0; i < n; i ++) a[i].r = read();
    for (int i = 0; i < m; i ++) b[i].r = read();
    fft(a, k, 1);
    fft(b, k, 1);
    for (int i = 0; i < k; i ++) c[i] = a[i] * b[i];
    fft(c, k, -1);
    for (int i = 0; i < n + m - 1; i ++)
        printf("%d ", (int)(c[i].r / k + 0.5));

    return 0;
}

倍增实现

// P3803 (AC)

#include <bits/stdc++.h>

using namespace std;

const double pi = acos(-1);

inline int read()
{
    int val = 0;
    bool si = 0;
    char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) si ^= ch == '-';
    for (;  isdigit(ch); ch = getchar())
        val = (val << 3) + (val << 1) + (ch ^ 48);
    return si == 0 ? val : -val;
}

const int N = 4e6 + 5;

int n, m, k, l;
int p[N];

struct cpl
{
    double r, i;

    cpl(double R = 0, double I = 0)
    {
        r = R;
        i = I;
    }

    friend cpl operator + (cpl a, cpl b) {return cpl(a.r + b.r, a.i + b.i); }
    friend cpl operator - (cpl a, cpl b) {return cpl(a.r - b.r, a.i - b.i); }
    friend cpl operator * (cpl a, cpl b) {return cpl(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r); }

} a[N], b[N], c[N];

inline void fft(cpl *f, int o)
{
    for (int i = 0; i < k; i += 1) if (i < p[i]) swap(f[i], f[p[i]]);
    for (int i = 1; i < k; i *= 2)
    {
        cpl s(cos(pi / i), sin(pi / i) * o);
        for (int j = 0; j < k; j += i << 1)
        {
            cpl w(1, 0), x, y;
            for (int t = 0; t < i; t ++, w = w * s)
                x = f[j + t],
                y = f[j + t + i] * w,
                f[j + t    ] = x + y,
                f[j + t + i] = x - y;
        }
    }
}

int main()
{
    n = read() + 1;
    m = read() + 1;
    for (k = 1; k < n + m; l ++, k <<= 1);
    for (int i = 0; i < k; i ++) p[i] = (p[i >> 1] >> 1) | ((i & 1) << l - 1);
    for (int i = 0; i < n; i ++) a[i].r = read();
    for (int i = 0; i < m; i ++) b[i].r = read();
    fft(a, 1);
    fft(b, 1);
    for (int i = 0; i < k; i ++) c[i] = a[i] * b[i];
    fft(c, -1);
    for (int i = 0; i < n + m - 1; i ++)
        printf("%d ", (int)(c[i].r / k + 0.5));

    return 0;
}

注意事项

注意 2 种实现的时间复杂度相同，但倍增常数更小
2 种实现都要求总项数为 2 的幂次，不足自行补齐
做完逆变换别忘了除以 $n$
复数运算可能有精度误差，要四舍五入

感谢阅读，有问题的话欢迎评论。qwq

posted @ 2025-12-09 18:48 nueryim 阅读(28) 评论(0) 收藏举报

刷新页面返回顶部

nueryim

笔记：快速傅里叶变换（FFT）

笔记：快速傅里叶变换（FFT）

概览

系数表示法

点值表示法

复数单位根

复数基础

单位根

离散傅里叶变换（DFT）

离散傅里叶逆变换（IDFT）

快速傅里叶变换和逆变换（FFT）

分治实现

倍增实现

P3803 【模板】多项式乘法（FFT）

分治实现

倍增实现

注意事项

公告