题解: AT_agc037_d_Sorting_a_Grid
题解: AT_agc037_d_Sorting_a_Grid
题意
题面很省流了,这里强调一点,本题 \(B\)、\(C\) 只要合法就行,因为可能有很多方案(显然)。
分析
看到这种构造方案的首先想到暴搜和网络流,这里 \(n\leq 100\) 暴搜的复杂度“爆”了,将思路往网络流上靠一靠。
注意到初始 \(A\)、目标 \(D\) 都为已知,因此就可以依靠这种定的关系建图。如果我们想知道方案,对于每个元素我们就要知道其在 \(B\) 或 \(C\) 中的行号、列号和值。
考虑 \(A\) 和 \(B\) 的关系:我们发现,\(A\) 和 \(B\) 每一整行的元素一定是相同的(不考虑顺序),因此在图中可以使用相同的节点表示 \(A\) 和 \(B\) 的行号(\(C\) 和 \(D\) 同理)。
考虑 \(B\) 和 \(C\) 的关系:我们发现,\(B\) 和 \(C\) 每一整列的元素一定是相同的,因此在图中可以使用相同的节点表示 \(B\) 和 \(C\)(当前列)的值,至于为什么要表示值而不是列号,往下读就知道了。
综上,参照第一个样例,我们可以建出大概这样一副图:
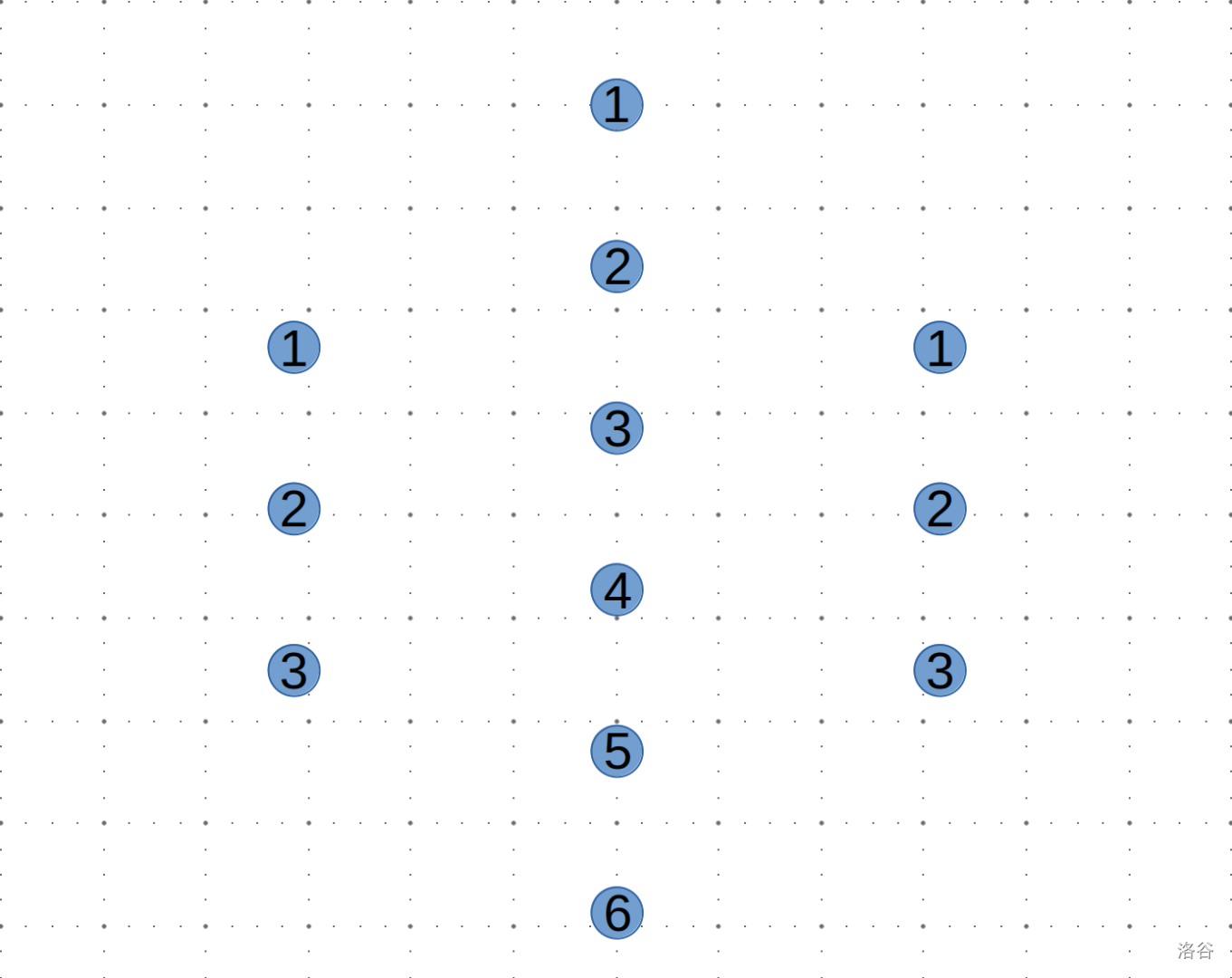
左边 \(3\) 个点表示 \(A\) 和 \(B\) 的行号,右边 \(3\) 个点表示 \(C\) 和 \(D\) 的行号,中间 \(6\) 个点则表示 \(B\) 和 \(C\) 的值。
因为 \(A\) 到 \(B\) 每行的元素相同,所以从 \(A\) 每行的行号向 \(B\) 每行(也就是 \(A\) 每行)的值连容量为 \(1\) 的边,表示 \(B\) 当前行可以存在 \(A\) 当前行的值。
因为 \(C\) 到 \(D\) 每行的元素也相同,所以 \(D\) 当前行的行号应从 \(C\) 当前行的所有值连容量为 \(1\) 的边,表示 \(C\) 当前行可以存在 \(D\) 当前行的值。
连完后图大概长这样:(边的容量都是一)
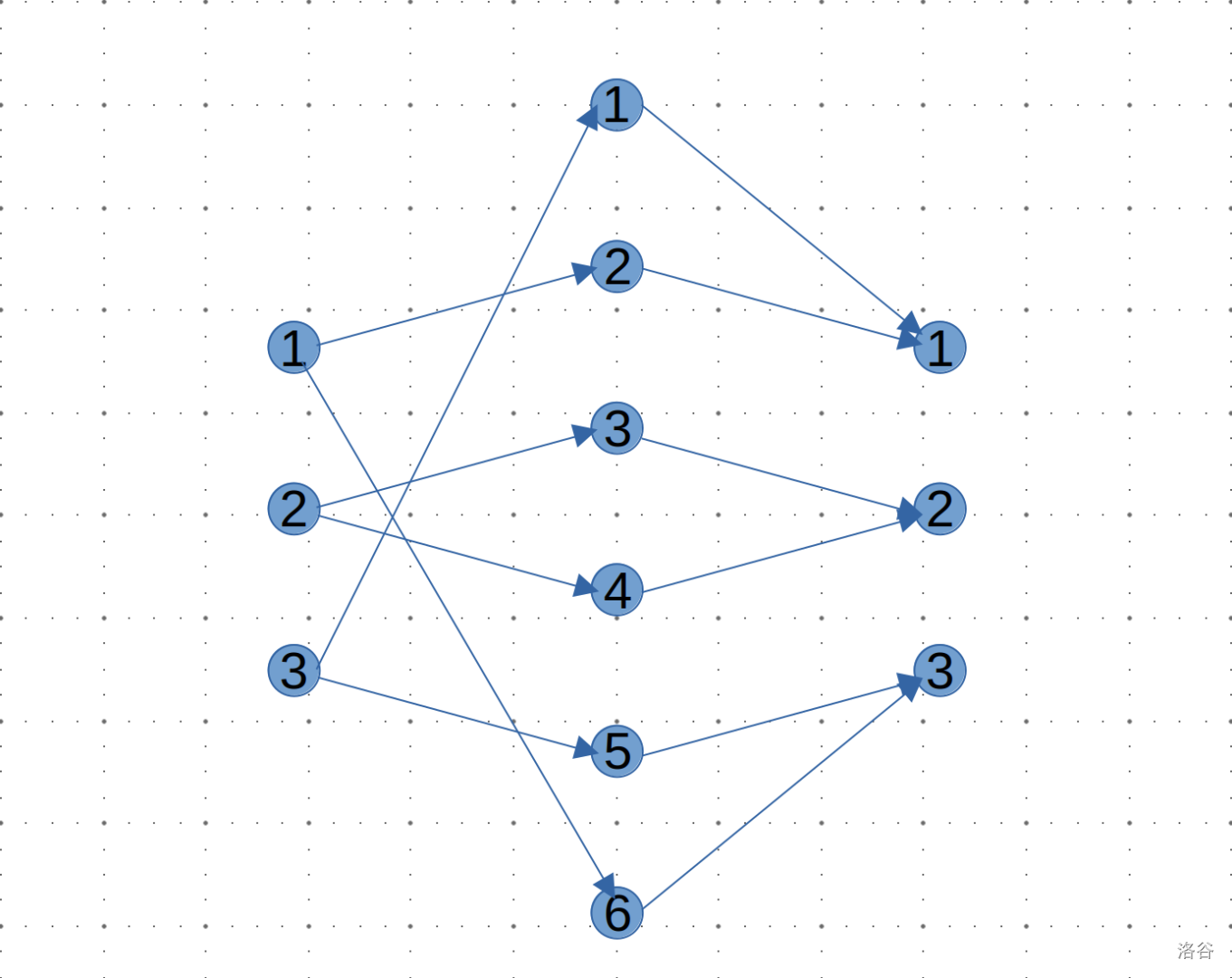
我们现在倒回来看看连完后的图代表着什么,例如一条路径:\(1\sim 6\sim3\) 就表示 \(B\) 中第一行值为 \(6\) 的元素在 \(C\) 中的第三行(值为 \(6\) 的元素在 \(B\) 中第一行,在 \(C\) 中第三行);路径:\(3\sim 5\sim 3\) 表示 \(B\) 中第三行值为 \(5\) 的元素在 \(C\) 中还是第三行。
一组(\(3\)条且没有公用节点)路径如:\(1\sim 6\sim 3\)、\(2\sim 3\sim 2\)、\(3\sim 1\sim 1\) 就表示 \(B\)、\(C\) 的这一列的元素为 \(6\)、\(3\)、\(1\)。图中可以分出两组路径,刚好就对应了矩阵的两列。
现在我们只需要知道如何给路径分组就能通过代入以上两个结论确定 \(B\) 和 \(C\) 的具体元素了。
那么如何分组呢?
我们发现如果给原图加上源点和汇点,那么一组恰好对应一个完美匹配,如图:(边的容量均为一)
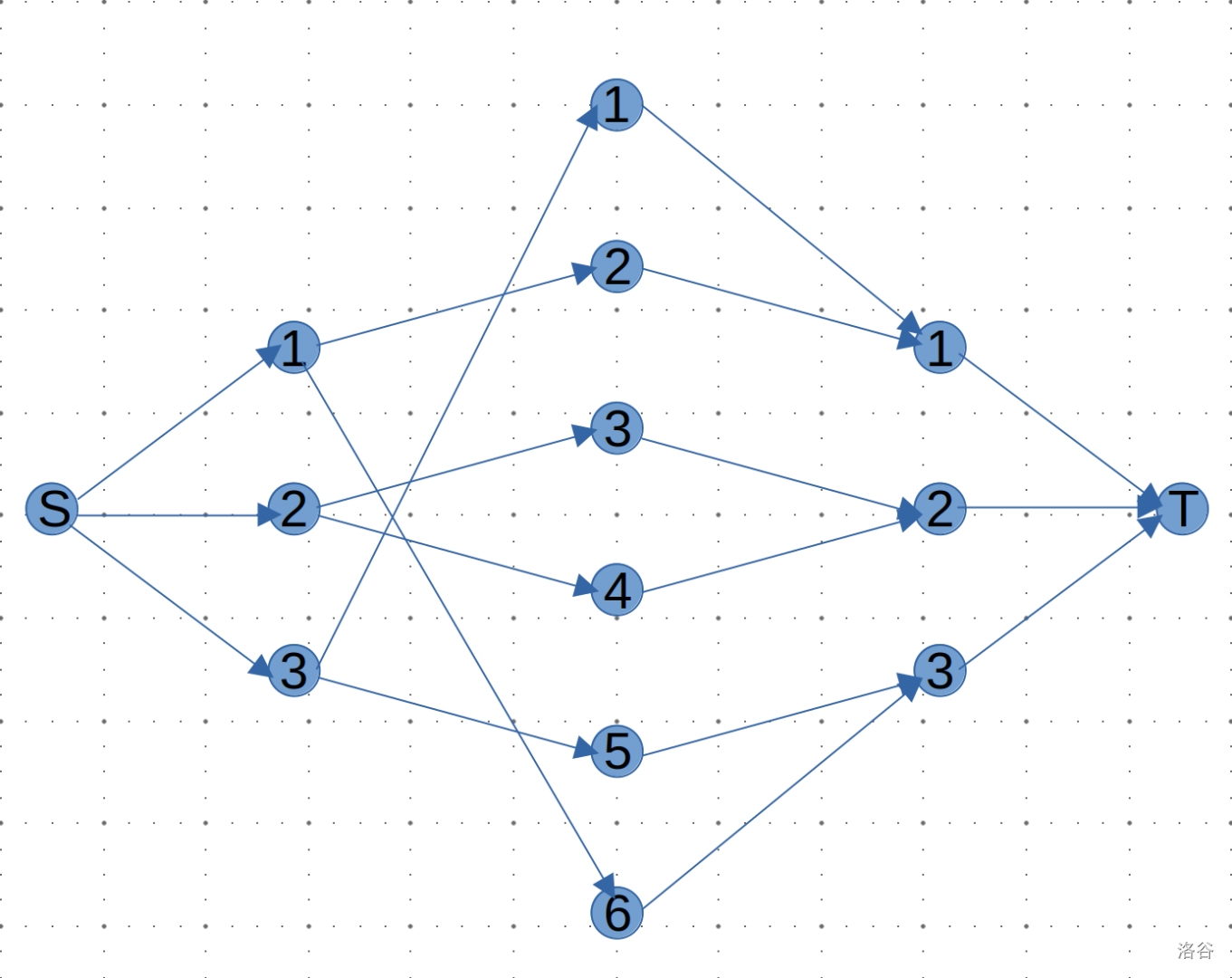
那么剩下的就简单了,跑 \(m\) 次最大流,每次统计方案即可。
代码
有几个细节强调一下:
- 每次跑完最大流要将直接连着源点和汇点的边的容量重置
- 统计答案时要将统计进答案的边加上标记
其他的就看代码吧:
//AT_agc037_d (AC)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
#define int long long
int read()
{
int res = 0, f = 1;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = -1;
for (; isdigit(ch); ch = getchar())
res = (res << 3) + (res << 1) + (ch ^ 48);
return res * f;
}
const int INF = 0x3f3f3f3f;
const int N = 1005; //开大点保险...
int n, m, a[N][N];
int pos(int num, int x) //左边的点num为1, 中间为0, 右边为2
{
if (num == 1)
return n * m + x;
if (num == 2)
return n * m + n + x;
return x;
}
int s, t, tot = 1, tota, totb, head[N * N + N * 2], cur[N * N + N * 2];
bool vis[N * N * 4];
struct edge
{
int to, nxt, flow;
} e[N * N * 4];
void add(int u, int v, int flow)
{
e[++ tot] = (edge) {v, head[u], flow};
head[u] = tot;
}
void build()
{
for (int i = 2; i <= tota; i += 2)
e[i].flow = 1, e[i ^ 1].flow = 0;
for (int i = totb; i <= tot; i += 2)
e[i ^ 1].flow = 1, e[i].flow = 0;
}
int dep[N * N + N * 2];
bool bfs()
{
memset(dep, 0, sizeof(dep));
queue <int> q;
dep[s] = 1;
q.push(s);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u], v, f; i; i = e[i].nxt)
{
if (vis[i] || vis[i ^ 1])
continue;
v = e[i].to, f = e[i].flow;
if (f && dep[v] == 0)
{
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t];
}
int dfs(int u, int flow)
{
if (u == t || flow == 0)
return flow;
int res = 0, tmp;
for (int &i = cur[u], v, f; i; i = e[i].nxt)
{
if (vis[i] || vis[i ^ 1])
continue;
v = e[i].to, f = e[i].flow;
if (dep[v] == dep[u] + 1 && (tmp = dfs(v, min(flow - res, f))))
{
res += tmp;
e[i].flow -= tmp;
e[i ^ 1].flow += tmp;
if (res == flow)
return res;
}
}
return res;
}
int dinic()
{
int res = 0, tmp;
while (bfs())
{
memcpy(cur, head, sizeof(cur));
while (tmp = dfs(s, INF))
res += tmp;
}
return res;
}
int cnt, ans1[N][N], ans2[N][N];
void stats()
{
cnt ++;
for (int u = 1; u <= n; u ++)
for (int i = head[pos(1, u)]; i; i = e[i].nxt)
if (!vis[i] && e[i].to < pos(1, u) && e[i].flow == 0)
{
vis[i] = vis[i ^ 1] = 1;
ans1[u][cnt] = e[i].to;
break;
}
for (int u = 1; u <= n; u ++)
for (int i = head[pos(2, u)]; i; i = e[i].nxt)
if (!vis[i] && e[i].to < pos(2, u) && e[i].flow == 1)
{
vis[i] = vis[i ^ 1] = 1;
ans2[u][cnt] = e[i].to;
break;
}
}
signed main()
{
n = read(), m = read();
s = n * m + n * 2 + 1, t = s + 1;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
a[i][j] = read();
for (int i = 1; i <= n; i ++)
add(s, pos(1, i), 1), add(pos(1, i), s, 0);
tota = tot;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
add(pos(1, i), a[i][j], 1), add(a[i][j], pos(1, i), 0);
for (int i = 1; i <= n; i ++)
for (int j = (i - 1) * m + 1; j <= i * m; j ++)
add(j, pos(2, i), 1), add(pos(2, i), j, 0);
totb = tot;
for (int i = 1; i <= n; i ++)
add(pos(2, i), t, 1), add(t, pos(2, i), 0);
for (int i = 1; i <= m; i ++)
{
build(); //重置源点和汇点的边的容量
dinic(); //跑最大流
stats(); //统计
}
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= m; j ++)
printf("%lld ", ans1[i][j]);
printf("\n");
}
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= m; j ++)
printf("%lld ", ans2[i][j]);
printf("\n");
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号