opengl基础学习.md
OpenGL学习
想学点图形学的东西,用于flutter的复杂动画(如果可能的话),再不济也能在Web上用用。
图形学主要有 OpenGL和Vulkun,但现有Vulkun教程大多默认你会OpenGL,就先看看OpenGL吧。
代码使用rust地址:https://gitee.com/muwuren/learn-opengl/
OpenGL
OpenGL是一个操作图形图像的API规范[1]。
所有版本的OpenGL规范文档都被公开的寄存在Khronos那里。有兴趣的读者可以找到OpenGL3.3(我们将要使用的版本)的规范文档。
模式
-
立即渲染模式(Immediate mode | 固定渲染管线):早期使用,大多功能都被库隐藏,开发者使用方便,但灵活度低。
-
核心模式(Core-profile):建议使用。灵活性高,但难于学习。
高版本OpenGL都是对低版本的扩展。
当使用新版本的OpenGL特性时,只有新一代的显卡能够支持你的应用程序。这也是为什么大多数开发者基于较低版本的OpenGL编写程序,并只提供选项启用新版本的特性。
扩展
if(GL_ARB_extension_name)
{
// 使用硬件支持的全新的现代特性
}
else
{
// 不支持此扩展: 用旧的方式去做
}
状态机
OpenGL本身是一个大状态机:一些系列变量描述此刻如何运行。状态即上下文(Context)。
- 状态设置函数(State-changing Function):更新上下文
- 状态使用函数(State-using Function):根据当前OpenGL的状态执行一些操作
对象
Object即一些选项的集合[2]。
// 创建对象
unsigned int objectId = 0;
glGenObject(1, &objectId);
// 绑定对象至上下文
glBindObject(GL_WINDOW_TARGET, objectId);
// 设置当前绑定到 GL_WINDOW_TARGET 的对象的一些选项
glSetObjectOption(GL_WINDOW_TARGET, GL_OPTION_WINDOW_WIDTH, 800);
glSetObjectOption(GL_WINDOW_TARGET, GL_OPTION_WINDOW_HEIGHT, 600);
// 将上下文对象设回默认
glBindObject(GL_WINDOW_TARGET, 0);
- 生成对象,并记录地址(objectId)
- 将对象绑定到上下文位置(这里是
GL_WINDOW_TARGET) - 设置当前绑定到 GL_WINDOW_TARGET 的对象(objectId)的一些选项
- 解绑
创建窗口
使用GLFW库。
# Cargo.toml
[package]
name = "opengl_study"
version = "0.1.0"
edition = "2024"
[dependencies]
gl = "0.14.0"
glfw = "0.59.0"
use gl::COLOR_BUFFER_BIT;
use glfw::{fail_on_errors, Action, Context, Glfw, Key, Modifiers, PWindow, Scancode, Window};
fn main() {
// 1. 初始化GLFW
let mut glfw = glfw::init(fail_on_errors).unwrap();
// 设置opengl version
glfw.window_hint(glfw::WindowHint::ContextVersion(3, 3));
glfw.window_hint(glfw::WindowHint::OpenGlProfile(glfw::OpenGlProfileHint::Core));
// 2. 创建窗口及上下文
let (mut window, events) = glfw.create_window(800, 600, "Hello, world!", glfw::WindowMode::Windowed)
.expect("Failed to create GLFW window");
// 3. 设置windows为当前上下文
window.make_current();
glfw.make_context_current(Some(&window));
window.set_key_polling(true);
load(&mut glfw);
window.set_framebuffer_size_callback(resize_window);
// 4. 事件循环
while !window.should_close() {
// 交换缓冲区
window.swap_buffers();
// poll
glfw.poll_events();
for (_, event) in glfw::flush_messages(&events) {
println!("{:?}", event);
match event {
glfw::WindowEvent::Key(key, scancode, action, modifiers ) => {
process_key(&mut window, key, scancode, action, modifiers );
} ,
_ => {}
}
}
}
// glfw.terminate() 由Drop自动完成
}
fn process_key(window: &mut PWindow, key: Key, scan_code: Scancode, action: Action, modifiers: Modifiers) {
if key == Key::Escape && action == Action::Press {
window.set_should_close(true);
}
if key == Key::C {
render();
}
}
fn resize_window(_win: &mut Window, width: i32, height: i32) {
unsafe {
gl::Viewport(0, 0, width, height);
}
}
fn load(glfw: &mut Glfw) {
gl::load_with(|s| glfw.get_proc_address_raw (s));
gl::Viewport::load_with(|s| glfw.get_proc_address_raw(s));
}
fn render() {
unsafe {
gl::ClearColor(0.3f32, 0.5f32, 0.1f32, 1.0f32);
gl::Clear(COLOR_BUFFER_BIT);
}
}
三角形
- 顶点数组对象 Vertex Array Object VAO
- 顶点缓冲对象 Vertex Buffer Object VBO
- 元素缓冲对象 Element Buffer Object EBO
- 索引缓冲对象 Index Buffer Object IBO
OpenGL中任何事物都在3D空间中,而屏幕是2D,OpenGL大部分工作都是将3D坐标转换为2D坐标。这个过程即图形渲染管线(Graphic Pipeline)。[3]
管线主要有两部:
- 将3D坐标转为2D坐标
- 将2D坐标转为有颜色的像素。
2D坐标和像素也是不同的,2D坐标精确表示一个点在2D空间中的位置,而2D像素是这个点的*似值,2D像素受到你的屏幕/窗口分辨率的限制。
管线可以被划分为几个阶段,每个阶段都会把前一阶段的输出作为输入。这些阶段被高度专门化,并容易并行。它们在GPU上为每一个(渲染管线)阶段运行各自的小程序(着色器(Shader))。OpenGL着色器为是有OpenGL着色器语言(OpenGL Shading Language, GLSL)写成的。
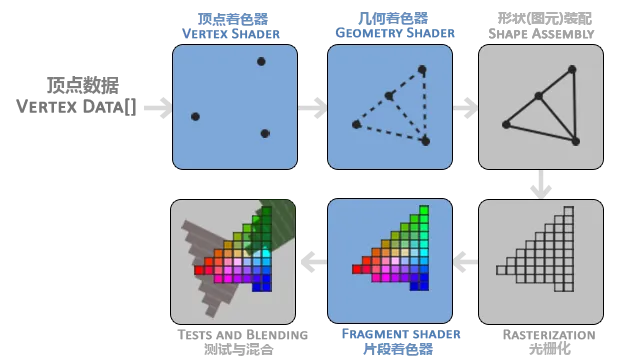
上图为图形渲染管线的每个阶段的抽象展示,蓝色部分可以自定义着色器。
上图步骤:
-
传递3个3D坐标作为输入,来表示一个三角形。这些数据叫做顶点数据(Vertex Data),是一系列顶点(Vertex)的集合。一个顶点的数据为顶点属性(Vertext Attribution)可以包含任何我们想要的数据。这里假设,每个顶点由一个3D位置和一些颜色组成。
图元(Primitive):用来描述OpenGL如何解释顶点属性。
任何一个绘制指令的调用都将把图元传递给OpenGL。这是其中的几个:GL_POINTS、GL_TRIANGLES、GL_LINE_STRIP。
-
顶点着色器(Vertex Shader):将输入3D坐标转换为另一种3D坐标,允许对顶点属性做一些基本处理。可以将输出选择性的传给几何着色器。
-
几何着色器(Geometry Shader): 将一组顶点作为输入,这些顶点形成图元,并且能够通过发出新的顶点来形成新的(或其他)图元来生成其他形状。
-
图元装配(Primitive Assembly):将顶点着色器(或几何着色器)输出的所有顶点作为输入(如果是GL_POINTS,那么就是一个顶点),并将所有的点装配成指定图元的形状
-
光栅化阶段(Rasterization Stage):把图元映射为最终屏幕上相应的像素,生成供片段着色器(Fragment Shader)使用的片段(Fragment)。在片段着色器运行之前会执行裁切(Clipping)。裁切会丢弃超出你的视图以外的所有像素,用来提升执行效率。
OpenGL中的一个片段是OpenGL渲染一个像素所需的所有数据。
-
片段着色器(Fragment Shader):主要目的是计算一个像素的最终颜色。通常,包含3D场景的数据(比如光照、阴影、光的颜色等等),这些数据可以被用来计算最终像素的颜色
-
Alpha测试和混合(Blending): 检测片段的对应的深度(和模板(Stencil))值(后面会讲),用它们来判断这个像素是其它物体的前面还是后面,决定是否应该丢弃。也会检查alpha值(alpha值定义了一个物体的透明度)并对物体进行混合(Blend)。所以,即使在片段着色器中计算出来了一个像素输出的颜色,在渲染多个三角形的时候最后的像素颜色也可能完全不同。
对于大多数场合,我们只需要配置顶点和片段着色器就行了。几何着色器是可选的,通常使用它默认的着色器就行了。
顶点输入
标准化设备坐标(Normalized Device Coordinates):OpenGL只处理范围为-1.0到1.0的坐标。与通常的屏幕坐标不同,y轴正方向为向上,(0, 0)坐标是这个图像的中心,而不是左上角。
通过glViewPort函数提供的数据,进行视口变换(Viewport Transform),标准化设备坐标会变为屏幕空间坐标(creen-space Coordinates)。
顶点缓冲对象(VBO):管理GPU内存(显存),存储一系列的顶点对象。使用缓冲原因,是因为CPU发送数据到GPU较慢。之后顶点着色器即可访问这些数据[4]。
// 顶点数据
float vertices[] = {
-0.5f, -0.5f, 0.0f,
0.5f, -0.5f, 0.0f,
0.0f, 0.5f, 0.0f
};
// 生成顶点缓冲区对象 使用唯一ID来记录
unsigned int VBO;
glGenBuffers(1, &VBO);
//绑定VBO
glBindBuffer(GL_ARRAY_BUFFER, VBO);
// 将顶点数据复制到缓冲内存中
// 参数4: 指定了我们希望显卡如何管理给定的数据
// GL_STATIC_DRAW :数据不会或几乎不会改变。
// GL_DYNAMIC_DRAW:数据会被改变很多。
// GL_STREAM_DRAW :数据每次绘制时都会改变。
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
顶点着色器
需要使用GLSL编写顶点着色器,然后编译。
// 版本 使用核心模式
#version 330 core
// in 在顶点着色器中声明所有的输入顶点属性(Input Vertex Attribute)
// location指明位置
layout (location = 0) in vec3 aPos;
void main()
{
// 向量数据类型
// gl_Position 即为输出,代表顶点向量
// 第4个参数代表向量方向
gl_Position = vec4(aPos.x, aPos.y, aPos.z, 1.0);
}
编译着色器
// 硬编码GLSL
const char *vertexShaderSource = "#version 330 core\n"
"layout (location = 0) in vec3 aPos;\n"
"void main()\n"
"{\n"
" gl_Position = vec4(aPos.x, aPos.y, aPos.z, 1.0);\n"
"}\0";
// 创建着色器对象 GL_VERTEX_SHADER表示创建顶点着色器
unsigned int vertexShader;
vertexShader = glCreateShader(GL_VERTEX_SHADER);
// 着色器源码附加到着色器对象上
glShaderSource(vertexShader, 1, &vertexShaderSource, NULL);
// 编译glsl
glCompileShader(vertexShader);
检测在调用glCompileShader后编译是否成功
int success; char infoLog[512]; // 获取是否成功 glGetShaderiv(vertexShader, GL_COMPILE_STATUS, &success); if(!success) { glGetShaderInfoLog(vertexShader, 512, NULL, infoLog); std::cout << "ERROR::SHADER::VERTEX::COMPILATION_FAILED\n" << infoLog << std::endl; }
片段着色器
片段着色器所做的是计算像素最后的颜色输出。
#version 330 core
// 输出结果 RGBA
out vec4 FragColor;
void main()
{
// RGBA
FragColor = vec4(1.0f, 0.5f, 0.2f, 1.0f);
}
编译着色器
//创建片段着色器对象
unsigned int fragmentShader;
fragmentShader = glCreateShader(GL_FRAGMENT_SHADER);
// 编译
glShaderSource(fragmentShader, 1, &fragmentShaderSource, NULL);
glCompileShader(fragmentShader);
着色器程序
着色器程序对象(Shader Program Object)是多个着色器合并之后并最终链接完成的版本。当链接着色器至一个程序的时候,它会把每个着色器的输出链接到下个着色器的输入。当输出和输入不匹配的时候,你会得到一个连接错误。
// 创建程序对象
unsigned int shaderProgram;
shaderProgram = glCreateProgram();
// 添加着色器
glAttachShader(shaderProgram, vertexShader);
glAttachShader(shaderProgram, fragmentShader);
// 链接
glLinkProgram(shaderProgram);
就像着色器的编译一样,我们也可以检测链接着色器程序是否失败,并获取相应的日志。
glGetProgramiv(shaderProgram, GL_LINK_STATUS, &success); if(!success) { glGetProgramInfoLog(shaderProgram, 512, NULL, infoLog); ... }
// 激活程序对象
glUseProgram(shaderProgram);
// 在把着色器对象链接到程序对象以后,记得删除着色器对象,我们不再需要它们了
glDeleteShader(vertexShader);
glDeleteShader(fragmentShader);
OpenGL还不知道它该如何解释内存中的顶点数据,以及它该如何将顶点数据链接到顶点着色器的属性上。我们需要告诉OpenGL怎么做。
链接顶点属性
我们必须在渲染前指定OpenGL该如何解释顶点数据。
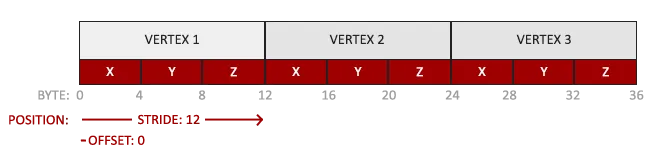
我们的顶点缓冲数据会被解析为下面这样子:
- 位置数据被储存为32位(4字节)浮点值。
- 每个位置包含3个这样的值。
- 在这3个值之间没有空隙(或其他值)。这几个值在数组中紧密排列(Tightly Packed)。
- 数据中第一个值在缓冲开始的位置。
// 使用glVertexAttribPointer函数告诉OpenGL该如何解析顶点数据
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);
glVertexAttribPointer参数:
-
要配置的顶点属性。在顶点着色器中使用
layout(location = 0)定义了position顶点属性的位置值(Location)。 -
定顶点属性的大小。顶点属性是一个
vec3,它由3个值组成,所以大小是3。 -
指定数据的类型,这里是GL_FLOAT(GLSL中
vec*都是由浮点数值组成的)。 -
是否希望数据被标准化(Normalize)。如果我们设置为GL_TRUE,所有数据都会被映射到0(对于有符号型signed数据是-1)到1之间。我们把它设置为GL_FALSE。
-
步长(Stride),它告诉我们在连续的顶点属性组之间的间隔。(译注: 这个参数的意思简单说就是从这个属性第二次出现的地方到整个数组0位置之间有多少字节)
-
位置数据在缓冲中起始位置的偏移量(Offset)。由于位置数据在数组的开头,所以这里是0。
每个顶点属性从一个VBO管理的内存中获得它的数据,而具体是从哪个VBO(程序中可以有多个VBO)获取则是通过在调用glVertexAttribPointer时绑定到GL_ARRAY_BUFFER的VBO决定的。由于在调用glVertexAttribPointer之前绑定的是先前定义的VBO对象,顶点属性
0现在会链接到它的顶点数据。
使用glEnableVertexAttribArray,以顶点属性位置值作为参数,启用顶点属性;顶点属性默认是禁用的。
// 0. 复制顶点数组到缓冲中供OpenGL使用
glBindBuffer(GL_ARRAY_BUFFER, VBO);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
// 1. 设置顶点属性指针
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);
// 2. 当我们渲染一个物体时要使用着色器程序
glUseProgram(shaderProgram);
// 3. 绘制物体
someOpenGLFunctionThatDrawsOurTriangle();
顶点数组对象
每当我们绘制一个物体的时候都必须重复上述过程,当物体很多时,会很复杂。
顶点数组对象(VAO)可以像顶点缓冲对象那样被绑定,任何随后的顶点属性调用都会储存在这个VAO中。
[!NOTE]
OpenGL的核心模式要求我们使用VAO,所以它知道该如何处理我们的顶点输入。如果我们绑定VAO失败,OpenGL会拒绝绘制任何东西。
一个顶点数组对象会储存以下这些内容:
- glEnableVertexAttribArray和glDisableVertexAttribArray的调用。
- 通过glVertexAttribPointer设置的顶点属性配置。
- 通过glVertexAttribPointer调用与顶点属性关联的顶点缓冲对象。
// 创建VAO
unsigned int VAO;
glGenVertexArrays(1, &VAO);
// 要想使用VAO,要做的只是使用glBindVertexArray绑定VAO。从绑定之后起,我们应该绑定和配置对应的VBO和属性指针,之后解绑VAO供之后使用。当我们打算绘制一个物体的时候,我们只要在绘制物体前简单地把VAO绑定到希望使用的设定上就行了。这段代码应该看起来像这样
// ..:: 初始化代码(只运行一次 (除非你的物体频繁改变)) :: ..
// 1. 绑定VAO
glBindVertexArray(VAO);
// 2. 把顶点数组复制到缓冲中供OpenGL使用
glBindBuffer(GL_ARRAY_BUFFER, VBO);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
// 3. 设置顶点属性指针
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);
[...]
// ..:: 绘制代码(渲染循环中) :: ..
// 4. 绘制物体
glUseProgram(shaderProgram);
glBindVertexArray(VAO);
someOpenGLFunctionThatDrawsOurTriangle();
三角形
glDrawArrays函数,它使用当前激活的着色器,之前定义的顶点属性配置,和VBO的顶点数据(通过VAO间接绑定)来绘制图元。
glUseProgram(shaderProgram);
glBindVertexArray(VAO);
glDrawArrays(GL_TRIANGLES, 0, 3);
元素缓冲区对象
元素缓冲对象(Element Buffer Object,EBO),也叫索引缓冲对象(Index Buffer Object,IBO)。 EBO是一个缓冲区,就像一个顶点缓冲区对象一样,它存储 OpenGL 用来决定要绘制哪些顶点的索引。
float vertices[] = {
0.5f, 0.5f, 0.0f, // 右上角
0.5f, -0.5f, 0.0f, // 右下角
-0.5f, -0.5f, 0.0f, // 左下角
-0.5f, 0.5f, 0.0f // 左上角
};
unsigned int indices[] = {
// 注意索引从0开始!
// 此例的索引(0,1,2,3)就是顶点数组vertices的下标,
// 这样可以由下标代表顶点组合成矩形
0, 1, 3, // 第一个三角形
1, 2, 3 // 第二个三角形
};
// 创建缓冲区对象
unsigned int EBO;
glGenBuffers(1, &EBO);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);
着色器
GLSL
着色器只是一种把输入转化为输出的程序, GPU中多个着色器之间并行运行,之间无法相互沟通。
GLSL格式要求:
- 开头需要有版本声明
- 输入、输出变量
uniform和main函数
#version version_number
in type in_variable_name;
in type in_variable_name;
out type out_variable_name;
uniform type uniform_name;
void main()
{
// 处理输入并进行一些图形操作
...
// 输出处理过的结果到输出变量
out_variable_name = weird_stuff_we_processed;
}
顶点着色器中,输入变量即为顶点属性(Vertex Attribute)。可以声明的顶点属性是有上限的,一般由硬件决定。OpenGL规定最少为16个。
数据类型
基本类型:
- int
- float
- double
- uint
- bool
容器类型:
- 向量 Vector
- 矩阵 Matrix
向量 Vector
GLSL中的向量是一个可以包含有2、3或者4个分量的容器,分量的类型可以是前面默认基础类型的任意一个。
| 类型 | 含义(n == 2 3 4) |
|---|---|
vecn |
包含n个float分量的默认向量 |
bvecn |
包含n个bool分量的向量 |
ivecn |
包含n个int分量的向量 |
uvecn |
包含n个unsigned int分量的向量 |
dvecn |
包含n个double分量的向量 |
向量取值可以为一下
| 序号 | 坐标取值 | 颜色取值 | 纹理取值 |
|---|---|---|---|
| 0 | x | r | s |
| 1 | y | g | t |
| 2 | z | b | p |
| 3 | w | a | q |
可以进行灵活取值,叫重组(Swizzling)
vec2 someVec;
vec4 differentVec = someVec.xyxx;
vec3 anotherVec = differentVec.zyw;
vec4 otherVec = someVec.xxxx + anotherVec.yxzy;
vec2 vect = vec2(0.5, 0.7);
vec4 result = vec4(vect, 0.0, 0.0);
vec4 otherResult = vec4(result.xyz, 1.0);
输入与输出
输入:in
输出:out
顶点着色器的输入是从顶点数据中直接接收输入,使用location指定输入变量。layout (location = 0)
片段着色器的输出要求为vec4。
如果我们打算从一个着色器向另一个着色器发送数据,我们必须在发送方着色器中声明一个输出,在接收方着色器中声明一个类似的输入。当类型和名字都一样的时候,OpenGL就会把两个变量链接到一起,它们之间就能发送数据了(这是在链接程序对象时完成的)
Uniform
uniform是另一种从CPU传递GPU数据的方式(顶点属性)。但Uniform是全局的,即必须在每个着色器程序对象中都是独一无二的,而且它可以被着色器程序的任意着色器在任意阶段访问。无论你把uniform值设置成什么,uniform会一直保存它们的数据,直到它们被重置或更新。
纹理 Textures
纹理是一张贴图,用于添加物体表面细节。为了能够把纹理映射(Map)到三角形上,我们需要指定三角形的每个顶点各自对应纹理的哪个部分。这样每个顶点就会关联着一个纹理坐标(Texture Coordinate),用来标明该从纹理图像的哪个部分采样。之后在图形的其它片段上进行片段插值(Fragment Interpolation)。
采样(Sampling):使用纹理坐标获取纹理颜色。坐标范围为[0, 1]。

纹理环绕方式
把纹理坐标设置在范围之外[0, 1]坐标之外行为:
| 环绕方式 | 描述 |
|---|---|
| GL_REPEAT | 对纹理的默认行为。重复纹理图像。 |
| GL_MIRRORED_REPEAT | 和GL_REPEAT一样,但每次重复图片是镜像放置的。 |
| GL_CLAMP_TO_EDGE | 纹理坐标会被约束在0到1之间,超出的部分会重复纹理坐标的边缘,产生一种边缘被拉伸的效果。 |
| GL_CLAMP_TO_BORDER | 超出的坐标为用户指定的边缘颜色。 |
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_MIRRORED_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_MIRRORED_REPEAT);
纹理过滤
纹理坐标不依赖于分辨率(Resolution),它可以是任意浮点值。所以OpenGL需要知道怎样将纹理像素(Texture Pixel,也叫Texel,译注1)映射到纹理坐标。
当物体大,但纹理小时,此时需要纹理过滤(Texture Filtering)。
-
临*过滤 GL_NEAREST:默认方式,取与中心点最接*的像素颜色值。会导致像素化

-
线性过滤 GL_LINEAR: 基于纹理坐标附*的纹理像素,计算出一个插值。一个纹理像素的中心距离纹理坐标越*,那么这个纹理像素的颜色对最终的样本颜色的贡献越大。整体更*滑。

效果:

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
多级渐远纹理 Mipmap
对远处物体处理时,需要对远处物体像素进行处理,这样节省内存与提高效率。
多级渐远纹理:在距离观察者超出一定阈值后,OpenGL使用这个处理,后一个纹理图像是前一个的二分之一。
在渲染中切换多级渐远纹理级别(Level)时,OpenGL在两个不同级别的多级渐远纹理层之间会产生不真实的生硬边界。就像普通的纹理过滤一样,切换多级渐远纹理级别时你也可以在两个不同多级渐远纹理级别之间使用NEAREST和LINEAR过滤。为了指定不同多级渐远纹理级别之间的过滤方式,你可以使用下面四个选项中的一个代替原有的过滤方式:
| 过滤方式 | 描述 |
|---|---|
| GL_NEAREST_MIPMAP_NEAREST | 使用最邻*的多级渐远纹理来匹配像素大小,并使用邻*插值进行纹理采样 |
| GL_LINEAR_MIPMAP_NEAREST | 使用最邻*的多级渐远纹理级别,并使用线性插值进行采样 |
| GL_NEAREST_MIPMAP_LINEAR | 在两个最匹配像素大小的多级渐远纹理之间进行线性插值,使用邻*插值进行采样 |
| GL_LINEAR_MIPMAP_LINEAR | 在两个邻*的多级渐远纹理之间使用线性插值,并使用线性插值进行采样 |
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
生成纹理
// 创建纹理对象
unsigned int texture;
glGenTextures(1, &texture);
// 绑定
glBindTexture(GL_TEXTURE_2D, texture);
// 生成纹理
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);
// 为当前绑定的纹理自动生成所有需要的多级渐远纹理
glGenerateMipmap(GL_TEXTURE_2D);
glTexImage2Dc参数:
- 纹理目标
- 为纹理指定多级渐远纹理的级别。0为默认级别
- 纹理储存的格式
- 宽
- 高
- 0 (历史遗留),总为0
- 原图形格式
- 数据类型
- 图像数据
纹理单元
使用glUniform1i,我们可以给纹理采样器分配一个位置值,这样的话我们能够在一个片段着色器中设置多个纹理。一个纹理的位置值通常称为一个纹理单元(Texture Unit)。一个纹理的默认纹理单元是0,它是默认的激活纹理单元。
参考代码:
https://gitee.com/muwuren/learn-opengl
commit: 纹理单元:多纹理赋值 368b4bb544b87015001ad1e365003c6b713fd474
变换
矩阵计算可以使图像变换更为简单。
向量
向量(Vector)最基本的定义就是一个方向。即向量 = 方向(direction) + 大小(magnitude)
下图中,向量\(\vec{w}\)和向量\(\vec{v}\)是相等的,因为其方向和大小(步长)相等
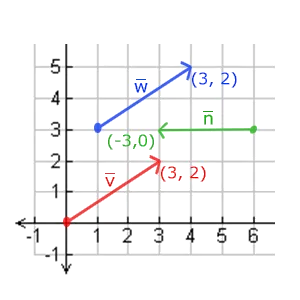
位置向量(Position Vector): 对向量添加一个postion,来确定具体位置。即表示 位置向量 = 方向 + 大小 + 位置
向量与标量运算
标量(Scalar):只是一个数字。当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:
\(\begin{pmatrix}a \\ b \\ c\end{pmatrix}\) + x = \(\begin{pmatrix} a+x \\ b+x \\ c+x \end{pmatrix}\)
注意-和÷运算时不能颠倒(标量-/÷向量),因为颠倒的运算是没有定义的。
数学上是没有向量与标量相加这个运算的,但是很多线性代数的库都对它有支持(比如说我们用的GLM)
向量取反
向量取反:可以理解为方向取反,比如东北方向->西南方向
\(-\vec{v}= -\begin{pmatrix} x \\ y \\ x \end{pmatrix} =\begin{pmatrix} -x \\ -y \\ -z \end{pmatrix}\)
向量加减
向量的加法可以被定义为是分量的(Component-wise)相加(减去),即将一个向量中的每一个分量加上(减去)另一个向量的对应分量:
加法[5]
\(\vec{v} + \vec{w} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \\ z_1+z_2 \end{pmatrix}\)
向量v = (4, 2)和k = (1, 2)可以直观地表示为:
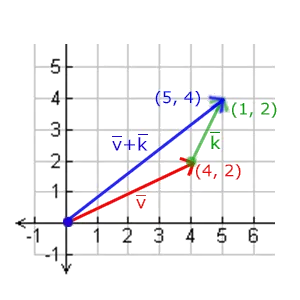
减法[6]
就像普通数字的加减一样,向量的减法等于加上第二个向量的相反向量:
\(\vec{v} - \vec{w} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} - \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} x_1-x_2 \\ y_1-y_2 \\ z_1-z_2 \end{pmatrix}\)
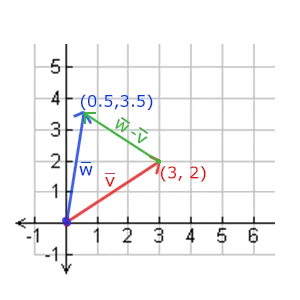
两个向量的相减会得到这两个向量指向位置的差。这在我们想要获取两点的差会非常有用。
长度
我们使用勾股定理(Pythagoras Theorem)来获取向量的长度(Length)/大小(Magnitude)。如果你把向量的x与y分量画出来,该向量会和x与y分量为边形成一个三角形:
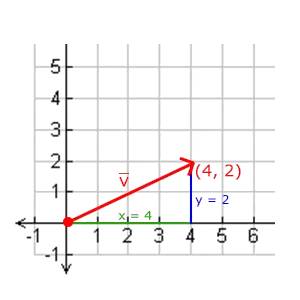
如果想知道\(\vec{v}\)的长度,则使用勾股定理计算:
\(\|\vec{v}\| = \sqrt{x^2+y^2}\)
以此推广至三维:
\(\|\vec{v}\| = \sqrt{x^2+y^2+z^2}\)
单位向量(unit vector):表示一个方向,但长度一直为1。即:
\(\hat{n} = \frac{\bar{v}}{\|\bar{v}\|}\)
这种方法叫做标准化(Normalizing),只关心方向不关心长度的时候使用。
向量相乘
普通乘法在向量上没有定义,因为在视觉上无意义。但有点乘(Dot Product)和叉乘(Cross Product)。
点乘(内积/数量积/标量积)
两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。
$\bar{v}\cdot \bar{w} = |\bar{v}| \cdot|\bar{w}| \cdot \cos\theta $
-
数学意义: 对于两个向量\(\vec{a} = (a_1, a_2, a_3, ..., a_n)\) 和\(\vec{b} = (b_1, b_2, b_3, ..., b_n)\),点乘运算为$\vec{a} \cdot \vec{b} = (a_1b_1, a_2b_2, ..., a_nb_n) $,结果是一个标量(无方向,只有大小) 。从公式看,是对应分量相乘后求和,这反映了向量在各维度上 “共同作用” 的累积效果。
-
几何意义: $\bar{v}\cdot \bar{w} = |\bar{v}| \cdot|\bar{w}| \cdot \cos\theta $ ,其中\(\theta\)是两向量的夹角。
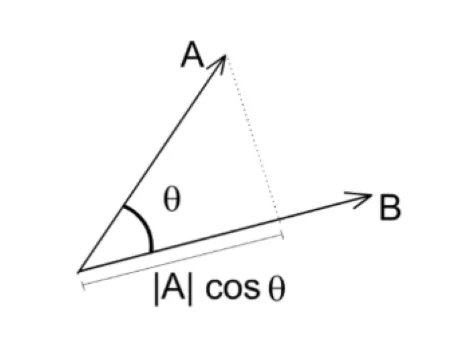
- \(\vec{v}\cdot\vec{w} > 0\): 夹角在0°到90°之间
- \(\vec{v}\cdot\vec{w} = 0\):则正交,相互垂直
- \(\vec{v}\cdot\vec{w} < 0\):方向基本相反,夹角在90°到180°之间
由此,也可以反推向量的\(\cos\theta\)值:
\(\cos\theta = \frac{\bar{v} \cdot \bar{w}} {\|\bar{v}\| \cdot \|\bar{w}\|}\)
叉乘(外积、史积)
叉乘只在3D空间中有意义,它需要两个不*行向量作为输入,生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。接下来的教程中这会非常有用。下面的图片展示了3D空间中叉乘的样子:
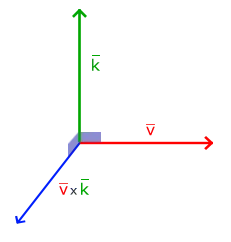
-
数学意义: \(\vec{a} = (a_1, a_2, a_3)\) 和\(\vec{b} = (b_1, b_2, b_3)\),叉乘运算为:
\[\vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = (a_2b_3 - a_3b_2)\vec{i} - (a_1b_3 - a_3b_1)\vec{j} + (a_1b_2 - a_2b_1)\vec{k} \]其中 \(\vec{i}\)、\(\vec{j}\)、\(\vec{k}\) 是空间直角坐标系中 \(x\)、\(y\)、\(z\) 轴的单位向量。
也可简化记为向量形式(直接给出各分量结果):
\[\vec{a} \times \vec{b} = (a_2b_3 - a_3b_2,\ a_3b_1 - a_1b_3,\ a_1b_2 - a_2b_1) \] -
几何意义:
- 方向:叉乘结果\(\vec{a} \times \vec{b}\)的方向垂直于\(\vec{a}\)和\(\vec{b}\)所在*面,且遵循右手定则:右手四指从\(\vec{a}\)向\(\vec{b}\)弯曲(转角不超过\(180^\circ\) ),竖起的大拇指方向就是\(\vec{a} \times \vec{b}\)的方向。这决定了叉乘结果的 “方向性”,是区分于点乘(标量结果)的核心特征。
- 大小:叉乘结果的模长\(\vert\vec{a} \times \vec{b}\vert = \vert\vec{a}\vert\vert\vec{b}\vert\sin\theta\)(\(\theta\)是\(\vec{a}\)与\(\vec{b}\)的夹角,\(0^\circ \leq \theta \leq 180^\circ\)。几何上,这等价于以\(\vec{a}\)和\(\vec{b}\)为邻边的*行四边形的面积。若将*行四边形沿对角线分割,也可理解为对应三角形面积的2倍(\(S_{\triangle} = \frac{1}{2}\vert\vec{a} \times \vec{b}\vert\)。
矩阵
矩阵通过行、列索引,每一项为矩阵的元素(Element)。
矩阵通过(i, j)来索引,其中 i是行,j是列。这与你在索引2D图像时的(x, y)相反。
矩阵加法
矩阵与标量加减:
注意,数学上是没有矩阵与标量相加减的运算的,但是很多线性代数的库都对它有支持(比如说我们用的GLM)。
矩阵与矩阵的加减:加法和减法只对同维度的矩阵才是有定义的。一个3×2矩阵和一个2×3矩阵(或一个3×3矩阵与4×4矩阵)是不能进行加减的。
矩阵的数乘
矩阵与标量之间的数乘:
现在我们也就能明白为什么这些单独的数字要叫做标量(Scalar)了。简单来说,标量就是用它的值缩放(Scale)矩阵的所有元素(译注:注意Scalar是由Scale + -ar演变过来的)
矩阵相乘
矩阵乘法基本上意味着遵照规定好的法则进行相乘[7]。相乘还有一些限制:
- 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。即 矩阵(i, j) * 矩阵 (j, k) = 矩阵(i, k)
- 矩阵相乘不符合交换律,即\(A \cdot B \ne B \cdot A\)
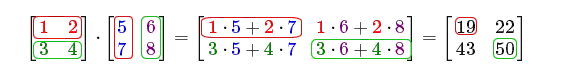
我们首先把左侧矩阵的行和右侧矩阵的列拿出来。这些挑出来行和列将决定我们该计算结果2x2矩阵的哪个输出值。如果取的是左矩阵的第一行,输出值就会出现在结果矩阵的第一行。接下来再取一列,如果我们取的是右矩阵的第一列,最终值则会出现在结果矩阵的第一列。这正是红框里的情况。如果想计算结果矩阵右下角的值,我们要用第一个矩阵的第二行和第二个矩阵的第二列(译注:简单来说就是结果矩阵的元素的行取决于第一个矩阵,列取决于第二个矩阵)
计算一项的结果值的方式是先计算左侧矩阵对应行和右侧矩阵对应列的第一个元素之积,然后是第二个,第三个,第四个等等,然后把所有的乘积相加,这就是结果了。现在我们就能解释为什么左侧矩阵的列数必须和右侧矩阵的行数相等了,如果不相等这一步的运算就无法完成了!
矩阵与向量相乘
向量实际就是一个\(N \times 1\)的矩阵,\(N\)是向量分量的个数,也叫\(N\)维向量。
矩阵\(M \times N\)与向量\(N \times 1\)相乘,结果是一个\(M \times 1\)的向量。用这个矩阵乘以我们的向量将变换(Transform)这个向量
单位矩阵
单位矩阵(Identity Matrix)是一个除对角线以外都是0的\(N \times N\)的矩阵,这种矩阵与向量相乘使向量完全不变:
你可能会奇怪一个没变换的变换矩阵有什么用?单位矩阵通常是生成其他变换矩阵的起点,如果我们深挖线性代数,这还是一个对证明定理、解线性方程非常有用的矩阵。
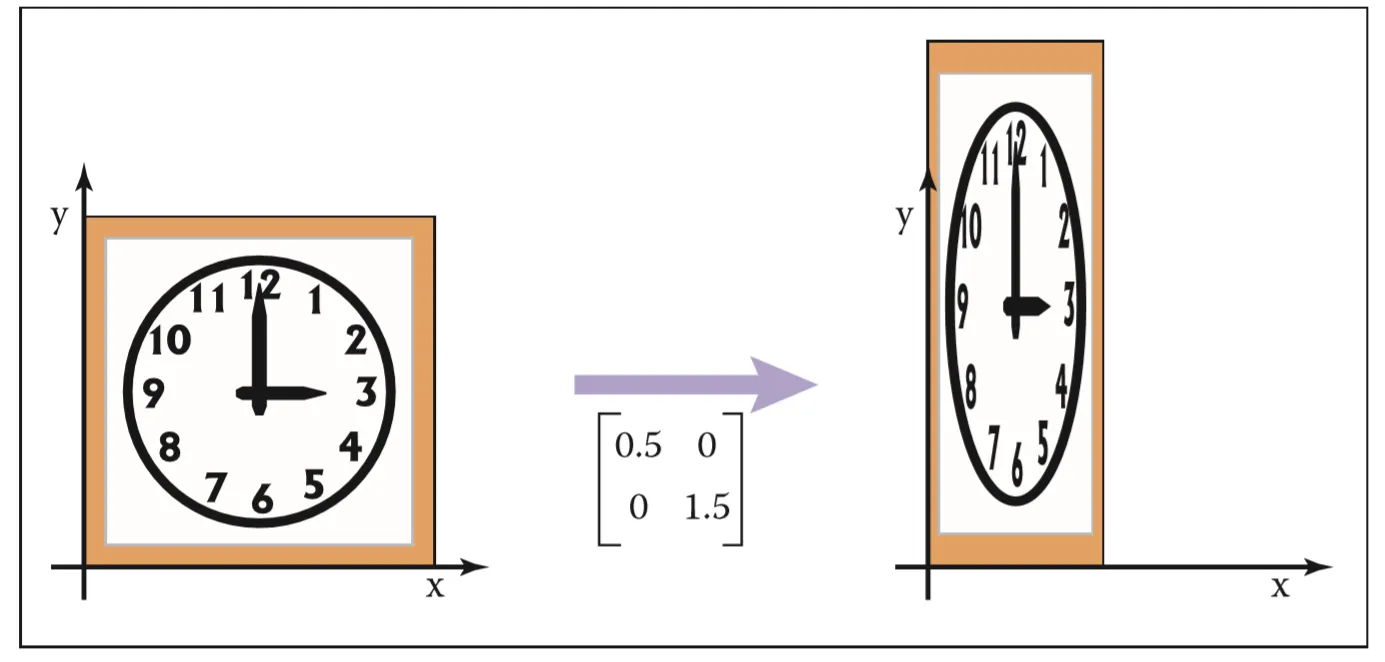
缩放
缩放(Scaling):对向量的长度进行缩放,而保持它的方向不变。
向量缩放就是改变这个箭头的 “长短”,但不改变它的方向(特殊情况除外,比如缩放系数为负时方向会反转 ) 。
通常说的 “向量缩放” 默认是 “均匀缩放”(所有分量乘以同一个 *k* ) 。但OpenGL里也有“非均匀缩放”(不同分量缩放系数不同 )。非均匀缩放是给每个分量乘以 不同的缩放系数。
我们从单位矩阵了解到,每个对角线元素会分别与向量的对应元素相乘。如果我们把缩放变量表示为\((S_1, S_2, S_3)\)我们可以为任意向量\((x,y,z)\)定义一个缩放矩阵:
位移
位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程。。我们已经讨论了向量加法,所以这应该不会太陌生。
和缩放矩阵一样,在4×4矩阵上有几个特别的位置用来执行特定的操作,对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为\((T_x, T_y, T_z)\),我们就能把位移矩阵定义为:
这样是能工作的,因为所有的位移值都要乘以向量的w行,所以位移值会加到向量的原始值上(想想矩阵乘法法则)。而如果你用3x3矩阵我们的位移值就没地方放也没地方乘了,所以是不行的:(如下所示,所以需要4x4矩阵)
齐次坐标(Homogeneous Coordinates)
向量的w分量也叫齐次坐标。想要从齐次向量得到3D向量,我们可以把x、y和z坐标分别除以w坐标。我们通常不会注意这个问题,因为w分量通常是1.0。使用齐次坐标有几点好处:它允许我们在3D向量上进行位移(如果没有w分量我们是不能位移向量的),而且下一章我们会用w值创建3D视觉效果。
如果一个向量的齐次坐标是0,这个坐标就是方向向量(Direction Vector),因为w坐标是0,这个向量就不能位移(译注:这也就是我们说的不能位移一个方向)。
旋转
2D或3D空间中的旋转2D或3D空间中的旋转用角(Angle)来表示。角可以是角度制或弧度制的来表示。
大多数旋转函数需要用弧度制的角,但幸运的是角度制的角也可以很容易地转化为弧度制的:
- 弧度转角度:
角度 = 弧度 * (180.0f / PI)- 角度转弧度:
弧度 = 角度 * (PI / 180.0f)
PI约等于3.14159265359。
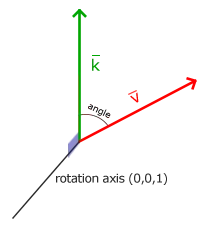
上图,向量\(\vec{v}\)是由向量\(\vec{k}\)向右旋转\(72^\circ\)(1/5圈)所得。
在3D空间中旋转需要定义一个角和一个旋转轴(Rotation Axis)。物体会沿着给定的旋转轴旋转特定角度。
使用三角学,给定一个角度,可以把一个向量变换为一个经过旋转的新向量。这通常是使用一系列正弦和余弦函数(一般简称sin和cos)各种巧妙的组合得到的。
旋转矩阵在3D空间中每个单位轴都有不同定义,旋转角度用θ表示:
- 沿X轴旋转:
-
沿y轴旋转:
\[\begin{bmatrix} \textcolor{red}{\cos\theta} & \textcolor{red}{0} & \textcolor{red}{\sin\theta} & \textcolor{red}{0} \\ \textcolor{green}{0} & \textcolor{green}{1} & \textcolor{green}{0} & \textcolor{green}{0} \\ \textcolor{blue}{-\sin\theta} & \textcolor{blue}{0} & \textcolor{blue}{\cos\theta} & \textcolor{blue}{0} \\ \textcolor{purple}{0} & \textcolor{purple}{0} & \textcolor{purple}{0} & \textcolor{purple}{1} \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \textcolor{red}{\cos\theta \cdot x + \sin\theta \cdot z} \\ \textcolor{green}{y} \\ \textcolor{blue}{-\sin\theta \cdot x + \cos\theta \cdot z} \\ \textcolor{purple}{1} \end{bmatrix} \] -
沿z轴旋转
\[\begin{bmatrix} \textcolor{red}{\cos\theta} & \textcolor{red}{-\sin\theta} & \textcolor{red}{0} & \textcolor{red}{0} \\ \textcolor{green}{\sin\theta} & \textcolor{green}{\cos\theta} & \textcolor{green}{0} & \textcolor{green}{0} \\ \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{1} & \textcolor{blue}{0} \\ \textcolor{purple}{0} & \textcolor{purple}{0} & \textcolor{purple}{0} & \textcolor{purple}{1} \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \textcolor{red}{\cos\theta \cdot x - \sin\theta \cdot y} \\ \textcolor{green}{\sin\theta \cdot x + \cos\theta \cdot y} \\ \textcolor{blue}{z} \\ \textcolor{purple}{1} \end{bmatrix} \]
下面这个公式,其中(R**x,R**y,R**z)代表任意旋转轴:
利用旋转矩阵我们可以把任意位置向量沿一个单位旋转轴进行旋转。也可以将多个矩阵复合,比如先沿着x轴旋转再沿着y轴旋转。但是这会很快导致一个问题——万向节死锁(Gimbal Lock)。
避免万向节死锁的真正解决方案是使用四元数(Quaternion),它不仅更安全,而且计算会更有效率
矩阵组合
根据矩阵之间的乘法,我们可以把多个变换组合到一个矩阵中。
假设我们有一个顶点(x, y, z),我们希望将其缩放2倍,然后位移(1, 2, 3)个单位。我们需要一个位移和缩放矩阵来完成这些变换。结果的变换矩阵看起来像这样:
当矩阵相乘时我们先写位移再写缩放变换的。矩阵乘法是不遵守交换律的,这意味着它们的顺序很重要。当矩阵相乘时,在最右边的矩阵是第一个与向量相乘的,所以你应该从右向左读这个乘法。比如,如果你先位移再缩放,位移的向量也会同样被缩放(译注:比如向某方向移动2米,2米也许会被缩放成1米)!
代码内容:
https://gitee.com/muwuren/learn-opengl
commit: 7cc49d823352ab0a697131f858437bb649ad65cd (矩阵变换)
坐标系统
将坐标变换为标准化设备坐标,接着再转化为屏幕坐标的过程通常是分步进行的,也就是类似于流水线那样子。在流水线中,物体的顶点在最终转化为屏幕坐标之前还会被变换到多个坐标系统(Coordinate System)。将物体的坐标变换到几个过渡坐标系(Intermediate Coordinate System)的优点在于,在这些特定的坐标系统中,一些操作或运算更加方便和容易,这一点很快就会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统:
- 局部空间(Local Space),或者叫 物体空间(Object Space)-->局部坐标
- 世界空间(World Space) --> 世界坐标
- 观察空间(View Space) --> 观察坐标
- 裁剪空间(Clip Space) --> 裁剪坐标
- 屏幕空间(Screen Space) --> 屏幕坐标
将一个空间坐标转为另一个空间坐标,需要几个变换矩阵,最重要的几个是 模型(Model)、观察(View)、投影(Projection)三个矩阵。
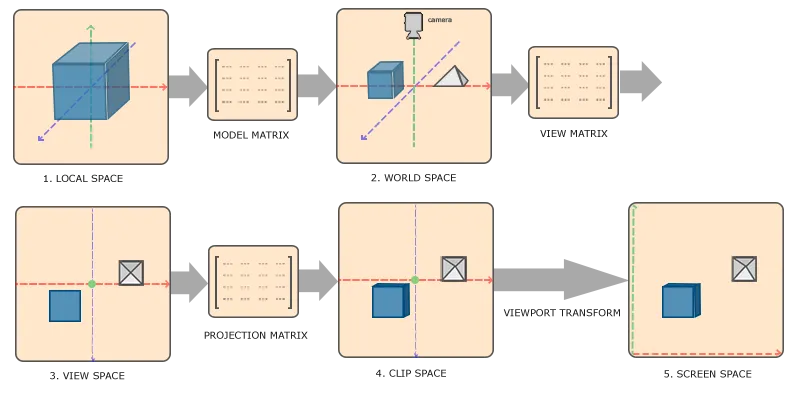
- 局部坐标是对象相对于坐标原点的坐标,也是物体的起始坐标
- 世界坐标,相对于世界的全局原点
- 观察坐标:从摄像机或者说是观察者的得到的坐标
- 裁剪坐标:将观察坐标投影的裁剪坐标,并判断哪些顶点会出现在屏幕上
- 屏幕坐标:从裁剪坐标到屏幕坐标被称为 视口变换(Viewport Transform)。
局部空间
局部空间是指物体所在的坐标空间,即对象最开始所在的地方。想象你在一个建模软件(比如说Blender)中创建了一个立方体。你创建的立方体的原点有可能位于(0, 0, 0),即便它有可能最后在程序中处于完全不同的位置。
世界空间
如果我们将我们所有的物体导入到程序当中,它们有可能会全挤在世界的原点(0, 0, 0)上,这并不是我们想要的结果。我们想为每一个物体定义一个位置,从而能在更大的世界当中放置它们。世界空间中的坐标正如其名:是指顶点相对于(游戏)世界的坐标。如果你希望将物体分散在世界上摆放(特别是非常真实的那样),这就是你希望物体变换到的空间。物体的坐标将会从局部变换到世界空间;该变换是由模型矩阵(Model Matrix)实现的。
模型矩阵是一种变换矩阵,它能通过对物体进行位移、缩放、旋转来将它置于它本应该在的位置或朝向。
观察空间
观察空间经常被人们称之OpenGL的摄像机(Camera)。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间。而这通常是由一系列的位移和旋转的组合来完成,*移/旋转场景从而使得特定的对象被变换到摄像机的前方。这些组合在一起的变换通常存储在一个观察矩阵(View Matrix)里,它被用来将世界坐标变换到观察空间。
裁剪空间
在一个顶点着色器运行的最后,OpenGL期望所有的坐标都能落在一个特定的范围内,且任何在这个范围之外的点都应该被裁剪掉(Clipped)。
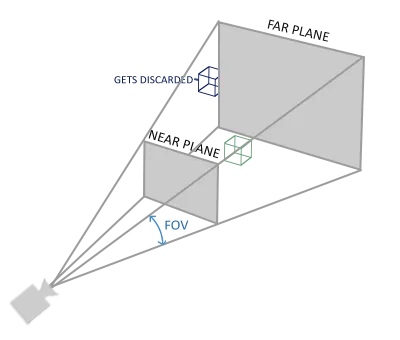
投影矩阵(Projection Matrix),它指定了一个范围的坐标,投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间,所以会被裁剪掉。
- 正射投影矩阵(Orthographic Projection Matrix)
- 透视投影矩阵(Perspective Projection Matrix)
*截头体(Frustum):由投影矩阵创建的观察箱(Viewing Box),每个出现在*截头体范围内的坐标都会最终出现在用户的屏幕上。
投影(Projection):将特定范围内的坐标转化到标准化设备坐标系的过程(而且它很容易被映射到2D观察空间坐标)
透视除法(Perspective Division):将4D裁剪空间坐标变换为3D标准化设备坐标的过程。在这个过程中我们将位置向量的x,y,z分量分别除以向量的齐次w分量;这一步会在每一个顶点着色器运行的最后被自动执行。
正射投影
正射投影矩阵定义了一个类似立方体的*截头箱,它定义了一个裁剪空间,在这空间之外的顶点都会被裁剪掉。创建一个正射投影矩阵需要指定可见*截头体的宽、高和长度。在使用正射投影矩阵变换至裁剪空间之后处于这个*截头体内的所有坐标将不会被裁剪掉。它的*截头体看起来像一个容器:
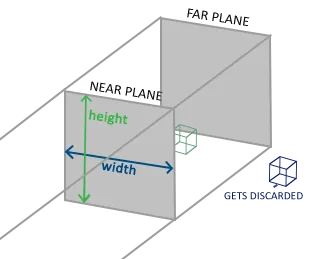
上面的*截头体定义了可见的坐标,它由宽、高、*(Near)*面和远(Far)*面所指定。任何出现在**面之前或远*面之后的坐标都会被裁剪掉。
要创建一个正射投影矩阵,我们可以使用GLM的内置函数glm::ortho:
// 参数1 + 参数2: 左右坐标
// 参数3 + 参数4: *截头体的底部和顶部
// 参数5 + 参数: **面和远*面的距离
glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);
正射投影矩阵直接将坐标映射到2D*面中,即你的屏幕,但实际上一个直接的投影矩阵会产生不真实的结果,因为这个投影没有将透视(Perspective)考虑进去。
透视投影
透视:*大远小
透视投影矩阵将给定的*截头体范围映射到裁剪空间,除此之外还修改了每个顶点坐标的w值,从而使得离观察者越远的顶点坐标w分量越大。被变换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的坐标都会被裁剪掉)。
顶点坐标的每个分量都会除以它的w分量,距离观察者越远顶点坐标就会越小。这是w分量重要的另一个原因,它能够帮助我们进行透视投影
在GLM中可以这样创建一个透视投影矩阵:
// 参数1: 表示的是视野(Field of View),并且设置了观察空间的大小。如果想要一个真实的观察效果,它的值通常设置为45.0f,
// 参数2: 设置了宽高比,由视口的宽除以高所得
// 参数3 + 参数4: *和远*面
glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);
组合
我们为上述的每一个步骤都创建了一个变换矩阵:模型矩阵、观察矩阵和投影矩阵。一个顶点坐标将会根据以下过程被变换到裁剪坐标:注意矩阵运算的顺序是相反的(记住我们需要从右往左阅读矩阵的乘法)
进入3D
-
先变换到世界坐标
glm::mat4 model; model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));通过将顶点坐标乘以这个模型矩阵,我们将该顶点坐标变换到世界坐标。我们的*面看起来就是在地板上,代表全局世界里的*面
-
变换为观察坐标:(观察矩阵)当在世界空间时,我们位于原点(0,0,0),将摄像机向后移动,和将整个场景向前移动是一样的。OpenGL是一个右手坐标系(Right-handed System),所以我们需要让摄像机沿着z轴的负方向移动
右手坐标系:
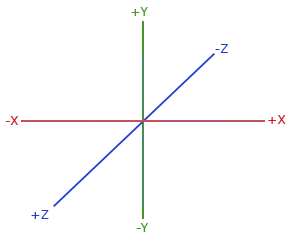
glm::mat4 view; // 注意,我们将矩阵向我们要进行移动场景的反方向移动。 view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f)); -
投影矩阵,我们希望在场景中使用透视投影
glm::mat4 projection; projection = glm::perspective(glm::radians(45.0f), screenWidth / screenHeight, 0.1f, 100.0f);
Z缓冲
OpenGL存储它的所有深度信息于一个Z缓冲(Z-buffer)中,也被称为深度缓冲(Depth Buffer)。深度值存储在每个片段里面(作为片段的z值),当片段想要输出它的颜色时,OpenGL会将它的深度值和z缓冲进行比较,如果当前的片段在其它片段之后,它将会被丢弃,否则将会覆盖。这个过程称为深度测试(Depth Testing),它是由OpenGL自动完成的。
glEnable(GL_DEPTH_TEST);
因为我们使用了深度测试,我们也想要在每次渲染迭代之前清除深度缓冲(否则前一帧的深度信息仍然保存在缓冲中)。就像清除颜色缓冲一样,我们可以通过在glClear函数中指定DEPTH_BUFFER_BIT位来清除深度缓冲:
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
代码:
commit: e3e947ed5b0f1aea2f3aee45879bf7770ae85404 坐标系统



 浙公网安备 33010602011771号
浙公网安备 33010602011771号