20244208 2024-2025-2《Python程序设计》实验四Python综合实践
20244208王子骞 2024-2025《Python程序设计》实验四Python综合实践
课程:《Python程序设计》
班级: 2442
姓名: 王子骞
学号:20244208
实验教师:王志强
实验日期:2025年5月13日
必修/选修: 专选课
一、实验要求和分析
(一)实验要求
Python综合应用:爬虫、数据处理、可视化、机器学习、神经网络、游戏、网络安全等。
例如:编写从社交网络爬取数据,实现可视化舆情监控或者情感分析。
例如:利用公开数据集,开展图像分类、恶意软件检测等
例如:利用Python库,基于OCR技术实现自动化提取图片中数据,并填入excel中。
例如:爬取天气数据,实现自动化微信提醒
例如:利用爬虫,实现自动化下载网站视频、文件等。
例如:编写小游戏:坦克大战、贪吃蛇、扫雷等等
(二)实验分析
技术说明
(为了用循环嵌套实现计算,孩子cpu都要烧掉了,大部分是自己写的,求求老师捞捞给个高分吧,球球力)
本学期数学课程学习了线性代数,本程序通过旨在通过python程序实现计算逆矩阵计算、行列式计算以及输入解线性方程组求解这三种线代基本运算。实现编程技术的跨学科应用。
本程序基于本学期学习内容,应用程序分支、for循环、定义函数、异常处理等技术
结合个人C++语言基础,运用二维数组与递归
通过尽可能简单的程序语言实现运算
(意思就是能暴力求解的地方都用暴力了,跑起来速度包炸裂的,但是文科生真的尽力了,跑起来没bug就烧高香了)
二、程序概述
在初始化时,
输入1则进入计算逆矩阵的程序分支;
输入2则进入行列式值的计算分支;
输入3则进入解线性方程组的分支。
程序以递归为主要运算逻辑,并加入了异常处理
程序内容与说明
第一步,定义需要使用的函数群
1.定义函数get_matrix(n):识别输入的方阵(主程序中,将n定义为矩阵阶数)
定义矩阵matrix,使用for循环,在各行中依每行的顺序输入元素
循环中,i为行数自变量,range(n)为范围

通过异常处理,判断矩阵内元素是否错误,预防程序崩溃
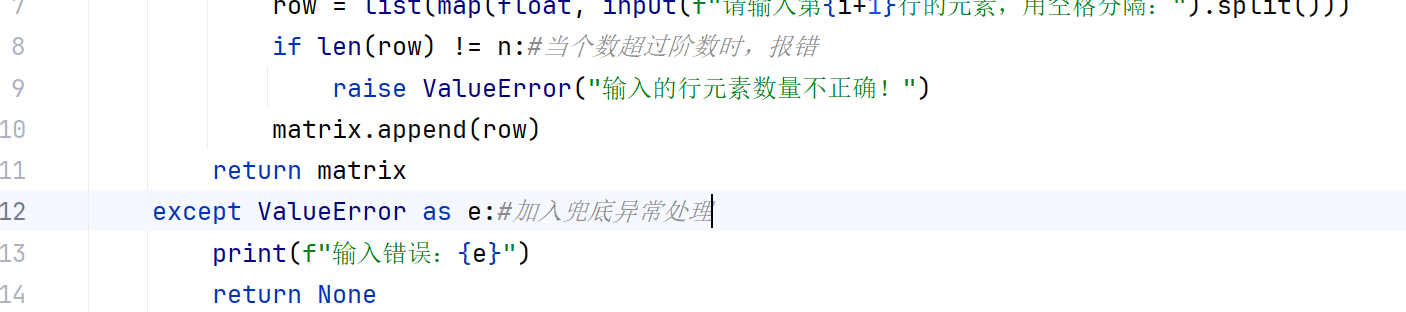
2.定义函数determinant(matrix):通过递归计算矩阵对应的行列式的值
对于1阶和2阶,使用二维数组,通过特殊解法,降低程序负载
并构建该递归的底层逻辑

对于高阶矩阵,通过for循环,依次读取子矩阵submatrix
row为子阵的行,在循环中读取并计入新的行new_row
c!=col即去掉对应元素所在的列

根据对应元素位置计算代数余子式的符号
通过本函数进入递归循环,将行列式逐步化简,最终回到二阶行列式计算

3.定义函数inverse_matrix(matrix):通过伴随矩阵的路径,计算逆矩阵
首先,判断矩阵对应的行列式的值是否为0
如值为0,直接break,减少程序负载

若不为0,进入下一步运算:
按照计算逆矩阵的方法,首先计算伴随矩阵
在循环中定义自变量i(行)j(列),通过一个大的双循环实现对矩阵内各位置依次遍历
再通过row和col的遍历,去掉对应行列以读取相应子矩阵,并加入新的matrix

这里通过4个for循环嵌套实现逐行逐列子矩阵的读取,打开并加入新的矩阵中
(为了用循环嵌套实现计算,孩子脑子都要烧掉了,求求老师捞捞给个高分吧,球球力)

同理,需要根据子矩阵对应位置控制正负号,求得代数余子式:

最后,通过计算并除以行列式的值,得到最终的逆矩阵
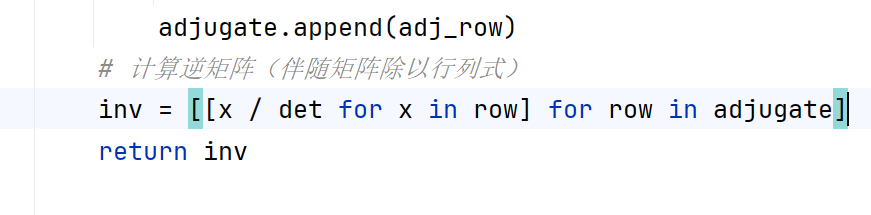
4.定义函数solve_equation(matrix,b):使用克拉默法则,求解线性方程组
将函数初始化,读取阶数与元素
并判断对应的行列式的值是否为0,如果是,则没有唯一解,提前结束运算以降低程序负载

将对应列的元素替换为常数项,生成新的矩阵(即克拉默法则中的分子)循环逻辑基本和第三个自定义函数相同
累了,不打了嘤嘤嘤

使用之前程序中的替换函数将矩阵转化为行列式的值

通过克拉默法则计算对应未知数的值,并返回答案solution

5.编译主程序main

通过输入0123实现程序的分支控制:
调用之前定义的函数读取输入的矩阵(各自定义函数已在前文说明,这里不再赘述)

输入1则进入计算逆矩阵的程序分支;

输入2则进入行列式值的计算分支;

输入3则进入解线性方程组的分支;

输入0退出程序

输入错误数字的报错

6.进入主程序main()

三、编程中遇到的困难
1.自变量繁多且复杂,随机分配不加注释会形成屎山代码
注意自变量命名具有一定的意义,如行命名为row,矩阵命名为matrix等
并及时添加注释,保证第二天醒来再看到程序不会导致左脑缺失指令集右脑缺失数据库
2.for循环嵌套最多达到4层,且在函数定义中使用了递归算法
对于for循环一定要通过注释搞清楚他在循环什么,本程序中往往会出现自变量和常数一起进循环的情况
这就会导致人脑内存崩溃,鉴定为内存条协议不兼容,电压不稳导致输出频率低下,建议去吃饭并更换一个适配的脑子
好吧,说实话还是应该用更高级的算法来解决,但能力有限哈哈
3.这个程序需要足够的线代理解,作为文科生真的尽力了
老师,菜菜,捞捞!
四、收获和感悟
(一)本次实验感悟
1.在实验设计中复习了高数的线代知识,实现跨学科融通交互,对未来的实际应用奠定了扎实基础,开辟蓝海业态;通过文科生特有的区位优势,找准差异化赛道(没和别人一样写游戏),锚定靶向生态位落位的关键方向
Ps:行管考不了研,在这里皮一下
2.认真怀疑每一个for循环的意义,最终成功对英语产生排异反应。在递归的路上实现运算器(脑子)与输出(手)的和解,并造成崩溃
3.本次实验综合运用了函数定义、for嵌套、列表、二维数组、递归等内容
主打一个菜,我但凡会别的算法哪还要用递归啊啊啊啊啊啊,疯了,都疯了。
这个故事告诉我们菜就多练
(二)课程总结
课程总结与建议
(一)课程收获与实践价值
本学期的Python课程为我的学习带来了显著提升,也给了我不少的思考
-
编程感悟
通过课堂实践,我不仅掌握了变量定义、条件判断、循环结构等基础知识,更能将这些技能转化为实用工具:课程中通过编写"猜数字""石头剪刀布"等趣味小游戏,在调试过程中体会逻辑构建的乐趣;开发电子日记本等生活化程序,感受代码解决实际问题的成就感……
作为文科生,在面对复杂程序逻辑时的无力感总让我感觉到与时代的脱节。
我深切的知道编程在这个时代的重要性,这是我报考这个学校的初衷。
第四次技术革命的锋芒指向的信息技术,我依旧能记起四年前我决定指向信息技术作为人生规划的那个起点,这个信念成为了在那段艰苦岁月里支撑我选择报考物理化学的动力
我也依旧能记起,三年前,由于无法适应高中物理化学的学习,被迫放弃信技专业规划时的无力感。
但我毕竟还是来到了这所学校,带着我微不足道的一点点编程基础。
在各种因素的一同作用下,也在一个理科院校的浓厚环境下,我决定开始向理科方向作出一点倾斜
不过是一点很小的尝试,现在我开始学习无线电了,不能不说是对过去理科情结的一点慰藉吧,多少受了这个学期编程学习一点影响。
所以我将学习信息技术视为我追逐时代的,一点微不足道的努力罢。 -
对于文科专业的编程学习,建议适度改变
我清楚的知道在我校文科专业开展编程教学的难度,但我总归希望能从中学到更多的东西,也希望能让以后的学弟学妹们受益
难度上讲,对于文科确实中规中矩,但是就现在的教学进度而言,过于缓慢了————
或者说,每节课讲授与实践的时间不太成比例,学的不够多,教的没精通
我非常清楚在我校我专业中开展有效教学的难度,但是,希望老师能给愿意学的学弟学妹们一个机会。
总的来说,王老师的课松弛有度,内容扎实,幽默风趣
感谢王老师在过去一个学期的付出。
五、视频链接:
https://www.bilibili.com/video/BV1yuJ8z4EBY/?vd_source=d7994f29e58b5aef7c29510eac4929e3
六、源代码如下:
点击查看代码
# 矩阵运算程序
def get_matrix(n):
"""获取n阶方阵"""
matrix = []#矩阵
try:
for i in range(n):#以浮点数的形式在各行中输入数字
row = list(map(float, input(f"请输入第{i+1}行的元素,用空格分隔:").split()))
if len(row) != n:#当个数超过阶数时,报错
raise ValueError("输入的行元素数量不正确!")
matrix.append(row)
return matrix
except ValueError as e:#加入兜底异常处理
print(f"输入错误:{e}")
return None
def determinant(matrix):#计算矩阵的行列式(递归)
n = len(matrix)
if n == 1:# 基本情况:1x1矩阵的行列式为其唯一元素
return matrix[0][0]
if n == 2:# 基本情况:2x2矩阵的行列式计算
return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]
det = 0
# 递归计算更高阶的行列式
for col in range(n):
# 生成子矩阵(去掉第一行和当前列)
submatrix = []
for row in range(1, n):
new_row = []
for c in range(n):
if c != col:
new_row.append(matrix[row][c])
submatrix.append(new_row)
# 计算代数余子式的符号
sign = (-1) ** col
# 递归调用行列式函数并累加
det += sign * matrix[0][col] * determinant(submatrix)
return det
def inverse_matrix(matrix):
"""计算矩阵的逆矩阵(使用伴随矩阵法)"""
n = len(matrix)
det = determinant(matrix)
if det == 0:
print("矩阵不可逆!")
return None
# 计算伴随矩阵
adjugate = []
for i in range(n):
adj_row = []
for j in range(n):
# 生成子矩阵(去掉第i行和第j列)
submatrix = []
for row in range(n):
if row != i:
new_row = []
for col in range(n):
if col != j:
new_row.append(matrix[row][col])
submatrix.append(new_row)
# 计算代数余子式
sign = (-1) ** (i + j)
cofactor = sign * determinant(submatrix)
adj_row.append(cofactor)
adjugate.append(adj_row)
# 计算逆矩阵(伴随矩阵除以行列式)
inv = [[x / det for x in row] for row in adjugate]
return inv
def solve_equations(matrix, b):
"""使用克拉默法则解线性方程组"""
n = len(matrix)
det = determinant(matrix)
if det == 0:
print("系数矩阵行列式为0,方程组无唯一解!")
return None
solutions = []
for i in range(n):
# 生成第i个替换矩阵(将第i列替换为常数项b)
replace_matrix = []
for row in range(n):
new_row = []
for col in range(n):
if col == i:
new_row.append(b[row])
else:
new_row.append(matrix[row][col])
replace_matrix.append(new_row)
# 计算替换矩阵的行列式
det_i = determinant(replace_matrix)
# 计算解
solutions.append(det_i / det)
return solutions
def main():
while True:
print("\n矩阵运算程序")
print("1. 计算逆矩阵")
print("2. 计算行列式值")
print("3. 解线性方程组")
print("0. 退出程序")
try:
choice = int(input("请输入选项(1/2/3/0):"))
if choice == 0:
print("程序已退出。")
break
elif choice in [1, 2, 3]:
n = int(input("请输入矩阵的阶数 n:"))
matrix = get_matrix(n)
if matrix is None:
continue
if choice == 1:
inv = inverse_matrix(matrix)
if inv is not None:
print("\n逆矩阵为:")
for row in inv:
print(row)
elif choice == 2:
det = determinant(matrix)
print(f"行列式值为:{det}")
elif choice == 3:
b = list(map(float, input("请输入常数项向量,用空格分隔:").split()))
if len(b) != n:
print("常数项向量长度不正确!")
continue
solutions = solve_equations(matrix, b)
if solutions is not None:
print("\n方程组的解为:")
for i, sol in enumerate(solutions):
print(f"x{i+1} = {sol}")
else:
print("输入无效,请输入 1/2/3/0!")
except ValueError:
print("输入错误,请输入数字!")
if __name__ == "__main__":
main()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号