算法导论之眼前一亮(持续更新)
本篇文章仅记录在平时刷题过程中,让人眼前一亮的处理思路,所以本篇文章适合算法爱好者阅读及参考,没有算法功底的程序猿们,建议不用花费太多的时间在本篇文章
1,题目描述:给定一个字符串数组,请根据“相同字符集”进行分组(摘自 LeetCode 49)
例 :Input: ["eat", "tea", "tan", "ate", "nat", "bat"],
Output:[
["ate","eat","tea"],
["nat","tan"],
["bat"]
]
基础分析:这类问题的常见处理并不难,只需要将每个字符记录对应值,内部循环比较,外部循环子串数组即可,时间复杂度 O(K2[子串平均长度] * N * Log(N)2)
晋级分析:我在基础之上,将字符串的和存了下来,将内部循环比较的次数降低,时间复杂度可以达到 O(K2 * N * Log(N) * Min(N)[代表字符串和相同的次数])
高级分析:首先引进一组概念:正整数唯一分解定理,每个大于1的自然数,要么本身为质数,要么可以由2个或以上的质数相乘,且组合唯一;上述定理结合问题来看,我们仅需要将字符串中的每个字符与质数一一对应,并将字符串所有字符对应的质数乘积保存下来,即可确保字符串的 hash 唯一,时间复杂度 O(K * N * Log(N))
Coding :
1 func GroupAnagramsOpt(strs []string) [][]string {
2 var res [][]string
3 strMap := make(map[int][]string)
4 prime := []int{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103}
5
6 for _, str := range strs {
7 sum := 1
8 for _, char := range str {
9 sum = prime[char-'a'] * sum
10 }
11 if _, ok := strMap[sum]; !ok {
12 strMap[sum] = []string{str}
13 } else {
14 strMap[sum] = append(strMap[sum], str)
15 }
16 }
17
18 for _, v := range strMap {
19 res = append(res, v)
20 }
21
22 return res
23 }
2,题目描述:给定一个 n,代表 n x n 的棋盘,摆放 n 个皇后,使其相互之间无法攻击(同一横竖斜仅一个旗子,8个皇后问题),返回所有的摆放情况(摘自 LeetCode 50)
例 :Input: 4
Output: [
[".Q..","...Q","Q...","..Q."],
["..Q.","Q...","...Q",".Q.."]
]
基础分析:采用递归法与回朔法,每次检查当前位置可否落子,落子后将当前位置所在的横竖斜 4 个方向全部置位不可落子,最终得出所有可能
晋级分析:对于 n x n 矩阵,不可落子不需要记录到具体的点,仅需要记录(行、列、左斜(i+j)、右斜(i-j+n))即可快速判断当前行,列、位置可否落子,省去记录和判断的时间复杂度
高级分析:我自己做的时候,发现一直在纠结重复性问题,所以第一版是在将结果放入队列时,进行重复排查,发现效率较低;再想通过递归的返回值,确定当前位置是否可以再次落子,以排除相同可能性,发现每次回溯后都必须处理标记数据;再后来发现每次递归的行,无需从 0 开始(同行仅有1个旗子),循环时不需要每次都从(0,0)点开始判断,节省相同摆法的重复性时间消耗。
Coding :
1 // 51. N-Queens 2 func SolveNQueens(n int) [][]string { 3 stepMap := make([][]bool, 3) 4 qMap := make([][]bool, n) 5 for i, _ := range stepMap { 6 stepMap[i] = make([]bool, 2*n) 7 } 8 for i, _ := range qMap { 9 qMap[i] = make([]bool, n) 10 } 11 12 t := &struct{ a [][]string }{a: make([][]string, 0)} 13 SolveNQueensSub(stepMap, qMap, t, n, 0) 14 return t.a 15 } 16 17 func SolveNQueensSub(stepMap [][]bool, qMap [][]bool, res *struct{ a [][]string }, n, i int) { 18 // trans to res 19 if i == n { 20 var vs []string 21 for _, row := range qMap { 22 v := make([]byte, n) 23 for i, r := range row { 24 if r { 25 v[i] = 'Q' 26 } else { 27 v[i] = '.' 28 } 29 } 30 vs = append(vs, string(v)) 31 } 32 res.a = append(res.a, vs) 33 return 34 } 35 36 for j := 0; j < n; j++ { 37 // col + / + \ 38 if !stepMap[0][j] && !stepMap[1][i+j] && !stepMap[2][j-i+n] { 39 qMap[i][j] = true 40 stepMap[0][j] = true 41 stepMap[1][i+j] = true 42 stepMap[2][j-i+n] = true 43 SolveNQueensSub(stepMap, qMap, res, n, i+1) 44 qMap[i][j] = false 45 stepMap[0][j] = false 46 stepMap[1][i+j] = false 47 stepMap[2][j-i+n] = false 48 } 49 } 50 }
3,题目描述:给定两个字符串 A,B,我们可以对 A 字符串进行 3 种操作。
“插入一个字符“
”替换一个字符“
”删除一个字符“
如何在最少的操作次数后,可以使 A 与 B 相等(摘自 LeetCode 72)
例 : input: “horse“,”ros“
output: 3(1,h -> r,"rorse";2,del 'r',"rose";3,del 'e',"ros")
基础分析:暴力法进行递归循环,每次成功后,记录次数返回最小次数,理论上是 n^3(这种方法我没有尝试,一般 leetcode 上的题目超过 n^2 的解法,往往都会超时,这里只是提出一种解法)
晋级分析:一般看到“最少”/"最大"/“最小”... 这类字眼,我们首先脑子中要冒出 4 个字“动态规划“,这是一个算法工程师的基本素质。这道题,我们如果用动态规划的思路去考虑,就会一目了然。"horse" 和 "ros" 的匹配,我们可以根据动态规划的思路去进行降级,分别求 "horse" 和 "ro"、"hors" 和 “ros”、 “hors” 和 “ro” 这三种情况下最小次数,这里我们将这三种情况分别称为 A、B、C 下的最小次数,则最终的最小次数与三种情况的结果息息相关。具体的关系静下心来推导:
A 情况:当前最小次数 + 1
B 情况:当前最小次数 + 1
C 情况:如果最后一位 'e' 和 's' 相等(这里只是提出假设),则返回当前最小次数,如果最后一位不相等,则返回当前最小次数 + 1
而我们需要的最小次数便是上面 3 种情况最小值。这里就可以给出公式
if str1[n] == str2[m] -> map[n][m] = min(map[n-1][m] + 1,map[n][m-1] + 1, map[n][m])
else -> map[n][m] = min(map[n-1][m] + 1,map[n][m-1] + 1, map[n][m] + 1)
当时做题时,根据这样的逻辑进行编码后,发现在跑测试用例时会计算少,为什么呢?其实能看到原因是第一列、第一行是有些特殊的,首先是没有 m-1、n-1 去比较计算,是能根据前一位判断当前的最小次数,这一行的逻辑是比较简单的,简单就是 "m" 和 "djfioncvohghmnhs" 的匹配,这里不详细给出推导,有些算法功底的同学应该是可以很快写出代码的,直接上代码
1 func MinDistanceV2(word1 string, word2 string) int { 2 if len(word1) == 0 { 3 return len(word2) 4 } 5 if len(word2) == 0 { 6 return len(word1) 7 } 8 9 n := len(word1) 10 m := len(word2) 11 disMap := make([][]int, n) 12 for i := 0; i < n; i++ { 13 disMap[i] = make([]int, m) 14 } 15 16 // first column 17 isUse := false 18 for i := 0; i < n; i++ { 19 disMap[i][0] = i + 1 20 if word1[i] == word2[0] { 21 isUse = true 22 } 23 if isUse { 24 disMap[i][0]-- 25 } 26 } 27 28 // first row 29 isUse = false 30 for i := 0; i < m; i++ { 31 disMap[0][i] = i + 1 32 if word1[0] == word2[i] { 33 isUse = true 34 } 35 if isUse { 36 disMap[0][i]-- 37 } 38 } 39 40 for i := 1; i < n; i++ { 41 for j := 1; j < m; j++ { 42 dis := Common.MAXINTNUM 43 if word1[i] == word2[j] { 44 if dis > disMap[i-1][j-1] { 45 dis = disMap[i-1][j-1] 46 } 47 } else { 48 if dis > disMap[i-1][j-1]+1 { 49 dis = disMap[i-1][j-1] + 1 50 } 51 } 52 if dis > disMap[i-1][j]+1 { 53 dis = disMap[i-1][j] + 1 54 } 55 if dis > disMap[i][j-1]+1 { 56 dis = disMap[i][j-1] + 1 57 } 58 disMap[i][j] = dis 59 } 60 } 61 return disMap[n-1][m-1] 62 }
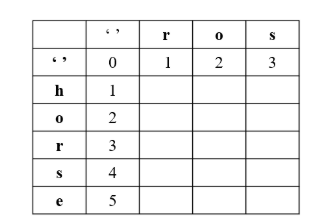
高级分析:有些人给出一些比较有趣的解法,相较于上述的解法并没有太多的优化,但多了一份巧妙。可以看到下图,既然第一行、第一列需要特殊处理,那可以在每个字符串前面加一列不存在的字符,初始化是使用 for 循环对第一行、第一列先进行简单赋值后再进行公式计算。(这里就不给出代码了,我个人使用的是第二种方法,之所以将这种方法列为高级分析,仅仅是解题思路需要适当的巧妙,可以让代码逻辑看起来简单很多)
4,题目描述:给定一个排序数组和一个目标值,找出数组中是否含有当前目标(摘自 LeetCode 81)
例 : input: [1,3,6,7,9];3
output: true
基础分析:根据原题,当时笨方法 for 循环,另一种业务中常用的方法便是二分查找法
晋级分析:之前参加过一个国内知名公司的面试,该公司比较注重算法,几乎每场面试都有一个算法题等着你,而我这次碰到的便是这道题的迭代,在原题的基础上将数组进行一次翻滚,将后面一部分(有可能是0-n)按顺序挪到数组前。在这种条件下,我也是没有任何怂,万物都有解决的办法嘛,大不了就是笨方法,但面试官肯定不会对这种笨方法有任何欣赏的点,肯定是需要二分查找法,最终也是利用1-3分钟将思路和代码写了出来。
很多人其实这里纠结的是每次选前半段还是后半段,其实我们进行拆分,就可以很明确的知道选择哪边;
1,判断当前中心是在翻滚点的左边还是右边,其实就是判断中间点的指是否大于最后一个值,大于则代表在翻滚点左侧,小于则代表在翻滚点右测(这第一步往往很重要,但经常有人考虑不到,包括我自己第一次的思路,因为两种不同的结果决定下面我们判断的方式)
2,当中点在翻滚点左侧时,我们只需要比较当前目标是否比首个数字大,如果大,则代表需要查前半段,否则就是后半段;相反,当中点在翻滚点右侧时,我们只需要比较当前目标是否比最后一个数字小,如果小,则代表需要查后半段,否则就是前半段
按上述两点进行循环,即可以 O(logn) 的时间复杂度得到结果
高级分析:当我看似艰难的将上面的代码写好之后(其实想的脑阔疼,改了好几版)。还未嚣张,面试官突然问如果数组中有重复的数字时,是否需要做什么修改。我考虑了几秒,觉得是没问题,面试官一笑就过了,我以为我的聪明征服了面试官大大,面试结束后兴起稍微写了一下代码在本地跑完之后,才发现有了重复测试案例后,结果是错误的。冥思苦想觉得异常丢人,并且想了好久的解决方法,其实很简单,在上面的解法之前做一次判断
1,当前中点是否与首位数组相等,相等则循环抛弃首位数组,start++;反之则是 end--;我们直接丢弃掉就可以啦,只是这种方案最坏时间复杂度就降到了 O(n)。上最终版代码
1 func Search(nums []int, target int) bool { 2 if len(nums) == 0 { 3 return false 4 } 5 6 start := 0 7 end := len(nums) - 1 8 for start <= end { 9 mid := (end-start)/2 + start 10 if nums[mid] == target { 11 return true 12 } 13 14 for start != mid && nums[mid] == nums[start] { 15 start++ 16 if start == mid { 17 start = mid + 1 18 goto OUT 19 } 20 } 21 for end != mid && nums[mid] == nums[end] { 22 end-- 23 if end == mid { 24 end = mid - 1 25 goto OUT 26 } 27 } 28 29 if nums[mid] < nums[end] { 30 if target > nums[mid] { 31 if target == nums[end] { 32 return true 33 } else if target < nums[end] { 34 start = mid + 1 35 end-- 36 } else { 37 end = mid - 1 38 } 39 } else { 40 end = mid - 1 41 } 42 43 } else { 44 if target < nums[mid] { 45 if target == nums[start] { 46 return true 47 } else if target > nums[start] { 48 start++ 49 end = mid - 1 50 } else { 51 start = mid + 1 52 } 53 } else { 54 start = mid + 1 55 } 56 } 57 OUT: 58 } 59 return false 60 }
5,题目描述:给定一个数组,每个数字代表当前位置的柱子高度,请返回柱子组成所能组成的最大高度(摘自 LeetCode 84)
例 : input: [3,1,5,4,1]
output: 选择 5,4 -> 4 * 2 = 8
基础分析:暴力美学,有用的就是好的方法,对任意两个位置遍历并每次计算两者之间的最低柱子,进行面积计算得出最大的面积,时间复杂度O(n3),按 leetcode 的尿性,这种复杂度是别想跑过测试用例的
晋级分析:上述的算法中,其实我们可以使用 n 的空间,来记录以当前为起点,后面柱子的最低高度,这样我们每次就可以省去找出两点之间高度的次数,时间复杂度O(n2),其实这种方法已经达到了一般算法喜好者的水准,可作为一名刷题者,这种方法只能让你通过面试,绝对达不到惊艳的地步。给出代码:
1 func LargestRectangleArea(heights []int) int { 2 if len(heights) == 0 { 3 return 0 4 } 5 6 highs := make([]int, 0, len(heights)) 7 res := 0 8 for i := 0; i < len(heights); i++ { 9 for j := 0; j < len(highs); j++ { 10 if highs[j] > heights[i] { 11 highs[j] = heights[i] 12 } 13 curArx := highs[j] * (i - j + 1) 14 if curArx > res { 15 res = curArx 16 } 17 } 18 if heights[i] > res { 19 res = heights[i] 20 } 21 highs = append(highs, heights[i]) 22 } 23 return res 24 }
高级分析:其实可以看到,上述的难点在于我们无法动态的滑动前后两端,保证每次滑动都为最优解,如果能够解决这个问题,我们就可以在 O(n)的时间下完成算法。其实换个角度想,向后滑动时,新的柱子高度如果大于等于上一个柱子,那尽管往上加,面积一定是大的;而如果下一个柱子比当前柱子小,则需要将前面所有的高柱子进行一次计算,得到这一部分的最大面积后,高的那些柱子已经失去意义了(可以将这一段比作一个区间,A-B 之间存在一些高柱子,A 比 B 小,那 A 前列的柱子和 B 后续的柱子无论如何都不可能再用到中间的高柱子,前列的直接按 A 的高度算,后续的直接按 B 的高度算)
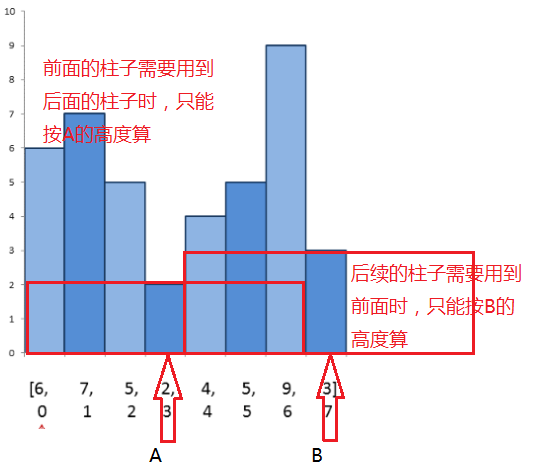
由前往后,又要由后往前计算并排除,直接使用栈工具,可以给出步骤:
1,对数组进行循环处理,循环 1,2,3 步,直到所有数组处理完毕
1,当前位置高度大于等于栈顶的数值时,直接 Push 到栈里面
2,当前位置高度小于栈顶数值时,进行 3 步骤循环,当栈为空或者栈顶数值小于当前位置高度,跳出循环
3,取出栈顶的数值,进行面积计算,公式:当前高度(h) * 两点距离
4,栈不为空时,说明还有需要处理的数据,这时候循环 5 步,直到栈为空
5,取出栈顶的数组,进行面积计算,公式:栈顶高度(h)* (数组长度 - 栈顶下标)
备注:栈中存储(下标,高度),防止最后一个数据未处理,可以提前插入一个 (-1,0) 的数据,当然也可以利用一些逻辑判断特殊处理
给出代码:
1 func LargestRectangleAreaOpt(heights []int) int { 2 if len(heights) == 0 { 3 return 0 4 } 5 stack := &Common.Stack{} 6 res := 0 7 8 type node struct { 9 index int 10 num int 11 } 12 stack.Push(&node{index: -1, num: 0}) 13 for i := 0; i < len(heights); i++ { 14 for stack.Size() > 1 { 15 top := stack.Top().(*node) 16 if heights[i] >= top.num { 17 break 18 } 19 20 stack.Pop() 21 nextTop := stack.Top().(*node) 22 area := top.num * (i - nextTop.index - 1) 23 if area > res { 24 res = area 25 } 26 } 27 stack.Push(&node{index: i, num: heights[i]}) 28 } 29 30 for stack.Size() > 1 { 31 top := stack.Pop().(*node) 32 nextTop := stack.Top().(*node) 33 area := top.num * (len(heights) - 1 - nextTop.index) 34 if area > res { 35 res = area 36 } 37 } 38 return res 39 }
6,题目描述:给定一个二维数组,每个位置给定 0 或 1,返回所能组成最大面积的矩阵(摘自 LeetCode 85)
例 : input: [1,0,1,1,0],[1,1,1,1,0]
output: 选择 2 * 2 或 1 * 4 = 4
基础分析:暴力解法,每个两个点之间进行判断,每次遍历两点所组成的矩形是否全部为 1,时间复杂度 O(n2m2)不用想了,除非不考虑性能才会这样做
晋级分析:动态规划,在对二维数据的循环过程中,分别记录其向上,向左的连续数量。判断公式:
if data[i][j] == 1 {left[i] = left[i-1]+1; right[j] = right[j-1] + 1} else {left[i] = 0; right[i] = 0},
这里可以将每个点的向左向右连续统计出来,而对于当前点的最大面积只需要对一个方向进行遍历求解即可,简单给出一张图
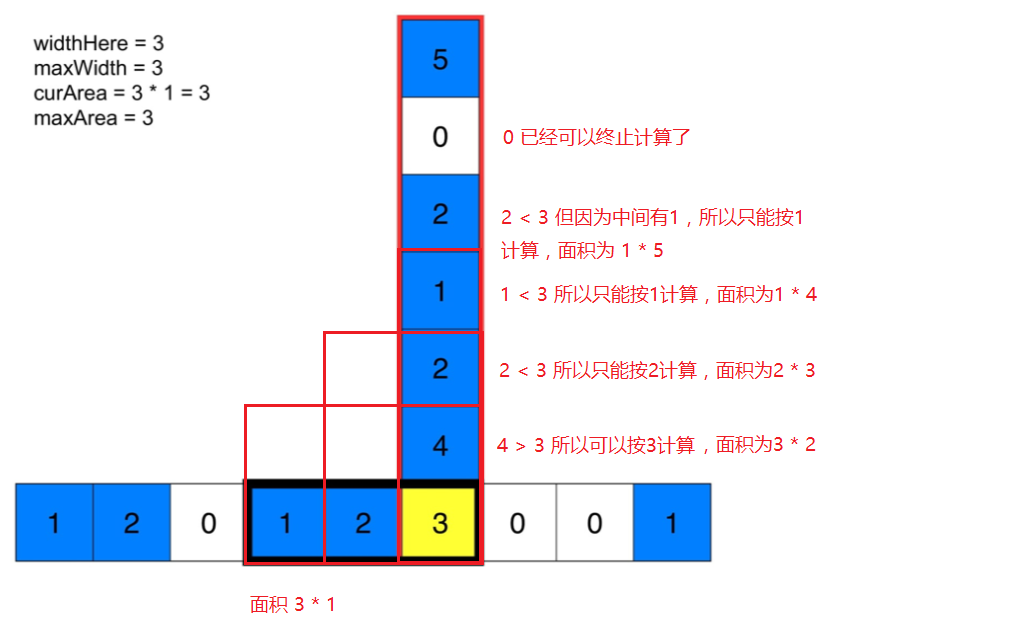
一个点从下往上循环计算,便可以的到当前点的最大面积,最终时间复杂度 O(n2m)
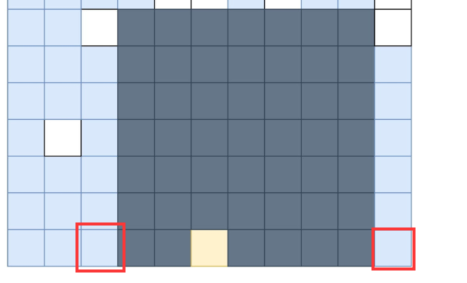
高级分析:动态规划,很厉害的一种算法,完全是没有想到的。这里给出别人的思路。每个点的面积(这里其实并不是最大面积),为当前点的最高高度,按最高高度扩展其宽度,算面积,如图

可以看到,黄点的面积可以如图所示计算,开始的时候我很纠结,这样并不是黄点的最大面积,但我忽略一个重要的问题
按新的面积计算方案,黄点的左右两侧总能找到最大的面积点,所以根据这个思路走下去,利用动态规划计算新的面积,每个点分别计算当前点的最高高度、高度对应的左侧范围,高度对应的右侧范围,公式分别为
if data[i][j] == 1 {height[i] = height[i]-1} else {height = 0}
if data[i][j] == 1 {left[i] = min(left[i-1], continue(左侧连续为1的数量)} else {left[i] = 0}
if data[i][j] == 1 {right[i] = min(right[i-1], continue(右侧连续为1的数量)} else {right[i] = 0}
给出代码:
1 func MaximalRectangle(matrix [][]byte) int { 2 if len(matrix) == 0 || len(matrix[0]) == 0 { 3 return 0 4 } 5 6 type node struct { 7 height int 8 left int 9 right int 10 } 11 res := 0 12 n := len(matrix) 13 m := len(matrix[0]) 14 nodeMat := make([][]node, n) 15 for i := 0; i < n; i++ { 16 nodeMat[i] = make([]node, m) 17 } 18 19 continueNum := 0 20 // full height and left 21 for i := 0; i < n; i++ { 22 for j := 0; j < m; j++ { 23 if matrix[i][j] == '1' { 24 continueNum++ 25 if i == 0 { 26 nodeMat[i][j].height = 1 27 } else { 28 nodeMat[i][j].height = 1 + nodeMat[i-1][j].height 29 } 30 31 if j == 0 { 32 nodeMat[i][j].left = 1 33 } else { 34 nodeMat[i][j].left = continueNum 35 if i != 0 && nodeMat[i-1][j].left != 0 && (nodeMat[i-1][j].left < nodeMat[i][j].left) { 36 nodeMat[i][j].left = nodeMat[i-1][j].left 37 } 38 } 39 } else { 40 continueNum = 0 41 } 42 } 43 continueNum = 0 44 } 45 46 // full right 47 for i := 0; i < n; i++ { 48 for j := m - 1; j >= 0; j-- { 49 if matrix[i][j] == '1' { 50 continueNum++ 51 if j == m-1 { 52 nodeMat[i][j].right = 1 53 } else { 54 nodeMat[i][j].right = continueNum 55 if i != 0 && nodeMat[i-1][j].right != 0 && (nodeMat[i-1][j].right < nodeMat[i][j].right) { 56 nodeMat[i][j].right = nodeMat[i-1][j].right 57 } 58 } 59 curArx := nodeMat[i][j].height * (nodeMat[i][j].right + nodeMat[i][j].left - 1) 60 if curArx > res { 61 res = curArx 62 } 63 } else { 64 continueNum = 0 65 } 66 } 67 continueNum = 0 68 } 69 70 return res 71 }
7,题目描述:给定一个数组,所有元素仅一个出现一次的值,其余均出现三次(摘自 LeetCode 137)
例 :input: 2,2,1,2
:out: 1
基础分析:暴力解法,遍历整个数组元素,使用一个 hash-map 存储所有的 key-num 值,当出现3次后移除指定的 key,最后仅留的一个 key 返回即可,时间复杂度为 O(N * 1),这里既是理论值 1,实际应用中 hash 解冲突、hash 定位均需要花费 O(1) 以上的时间。
晋级分析:位运算,其实位运算除了用来做运算符之外,还有需要其他的用途,比如模拟乘法、判断数值是否为2的幂次方、判断一个数的二进制有多少位是1...诸如此类,有兴趣的可以到 https://www.zhihu.com/question/38206659 了解一下。
其实说到位运算可能有些了解的同学已经有反应过来,那就是当其余元素均出现两次的情况,我们就可以通过^(按位异或)的运算符,遍历整个数组,即可消除所有相同的元素,最后仅保留一个仅出现元素;那回来再看,我们如何利用运算符去抵消出现三次的元素呢;我们可以通过多个运算符,模拟出三进制的情形(实际计算机中既不存在三进制、更不存在三进制的位运算,我们只是想办法去模拟 出现三次抵消掉 而已)
1,使用变量 a 记录个位的数值(二进制的 1),使用变量 b 记录复位的数值(二进制的 2)
2,当遍历数值某一个位为 1 时,分别判断 3,4
3,当变量 b 的当前位为 1,则说明已经当前位已经出现过 2 次,则本次直接抵消,即 b 和 a 的当前位均置 0
4,否则当变量 a 的当前位为 0,则改变变量 a 的当前位为 1,
5,否则即变量 a 的当前位为 1,则修改变量 a 的当前位为 0,修改变量 b 的当前位为 1
6,遍历结束后,返回 a 即可
上述逻辑看似复杂,但实际代码中,无需对每位进行判断,只需使用位运算代理上述逻辑,给出代码:
1 func SingleNumberV2Opt(nums []int) int { 2 a := 0 3 b := 0 4 5 for _, num := range nums { 6 tmp := a & num // 得到需要进位的位数字 7 a = a ^ num // 计算当前 a 的最终值 8 b = b ^ tmp // 计算当前 b 的最终值 9 10 tmp = a & b // 得到 a 和 b 均为 1 的位 11 a = a - tmp // 消除出现三次的位 12 b = b - tmp // 消除出现三次的位 13 } 14 15 return a 16 }
用心写代码,Refuse copy on coding,Refuse coding by butt.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号