卷积神经网络基础之百度飞浆课程笔记

卷积神经网络基础之百度飞浆课程笔记

卷积神经网络的基础知识主要有卷积、池化、激活函数、批归一化和Dropout等理论和技巧共五部分，下面将逐一展开进行介绍。（下文中可能部分公式无法正常显示，我有联系博客园客服，他们说在chrome和firefox浏览器上看都是正常的，可是我在chrome上看还是有些问题，多方询问求解也没解决这个问题，非常抱歉，如果您有好的解决办法请在评论区留言，非常感谢！！！）

卷积（Convolution）

卷积计算

卷积在数学中是一种积分变换的方法，可能大家对这个也不太关心，在卷积神经网络中，卷积层的实现方式实际上是数学中定义的互相关运算，通常是用滑动窗口的点积运算来完成，如下图 卷积计算过程（来自百度飞浆深度学习课程）：

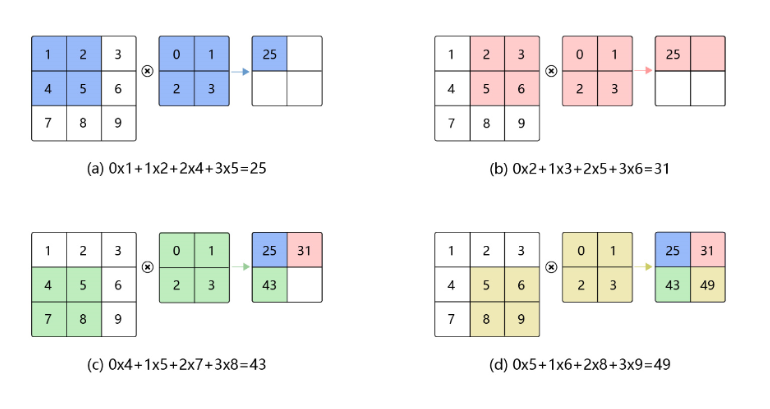
上图中的0、1、2、3组成的矩阵就叫做卷积核，一个卷积算子除了进行上述的卷积计算之外，还包括加上偏置项的操作，即在卷积计算的结果基础上加上一个常数项。

卷积输出特征图的尺寸计算公式如下：

\[\begin{aligned} H_{\text {out}} &=H-k_{h}+1 \\ W_{\text {out}} &=W-k_{w}+1 \end{aligned} \]

\(H\)表示输入图片的高度，\(W\)表示输入图片的宽度，\(k_{h}\) 表示卷积核的高度，\(k_{w}\)表示卷积核的宽度，\(1\) 表示偏置项，\(H_{out}\)表示输出尺寸的高，\(W_{out}\)表示输出尺寸的宽。（尺寸计算一定要会，很基础也很重要）

填充（padding）

在卷积计算中，我们知道经过卷积之后，输出尺寸是在变小的，为了避免卷积之后图片尺寸不断变小，通常会在图片的外围进行填充操作，从而保证尺寸的固定，如下图所示（来源于百度飞浆）：

如上图（a）所示，填充的大小为1，使得输入图片尺寸由4 x 4变为6 x 6，根据上述卷积尺寸计算公式，经过卷积之后输出尺寸变为4 x 4。

加入padding后卷积输出特征图的尺寸计算公式如下：

如果在图片高度方向，在第一行之前填充 \(p_{h1}\) 行，在最后一行之后填充 \(p_{h2}\) 行；在图片的宽度方向，在第1列之前填充\(p_{w1}\)列，在最后1列之后填充\(p_{w2}\)列；则填充之后的图片尺寸为\((H+p_{h1}+p_{h2})×(W+p_{w1}+p_{w2})\)。经过大小为\(k_h\times k_w\)的卷积核操作之后，输出图片的尺寸为：

\[\begin{array}{l} H_{\text {out}}=H+p_{h 1}+p_{h 2}-k_{h}+1 \\ W_{\text {out}}=W+p_{w 1}+p_{\text {w} 2}-k_{w}+1 \end{array} \]

在卷积计算过程中，通常会在高度或者宽度的两侧采取等量填充，即\(p_{h1} = p_{h2} = p_h\),\(p_{w1} = p_{w2} = p_w\),，上面计算公式也就变为：

\[\begin{aligned} H_{\text {out}} &=H+2 p_{h}-k_{h}+1 \\ W_{\text {out}} &=W+2 p_{w}-k_{w}+1 \end{aligned} \]

这应该是经常会看到的公式的样子，实际中，卷积核通常使用1，3，5，7这样的奇数，通过上述等式，如果我们想要卷积后的图像尺寸不变，则可以得到填充大小为\(p_h=(k_h-1)/2\)，\(p_w=(k_w-1)/2\)，这也是我们经常会在设计卷积网络模型时需要进行的尺寸计算。

步幅（stride）

卷积层的参数步幅简单来说就是在卷积计算中，滑动窗口每次滑动的距离，很好理解，直观来看如下图：

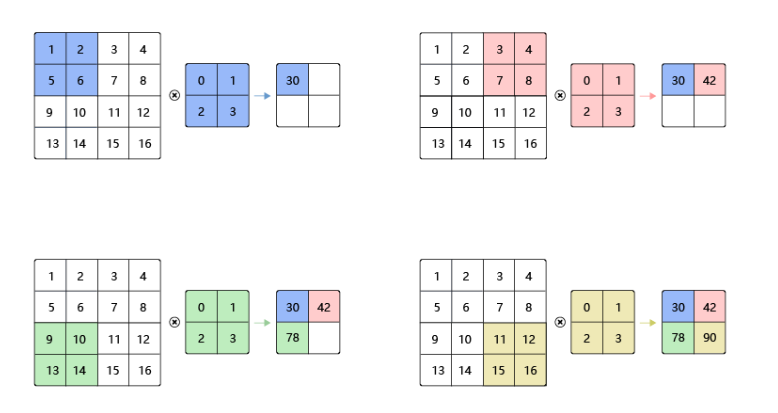
步幅分为两个方向，分别是高\(s_h\)和宽\(s_w\)，通常都设置为一样的大小。

加入stride后卷积输出特征图的尺寸计算公式如下：

\[\begin{aligned} H_{\text {out}} &=\frac{H+2 p_{h}-k_{h}}{s_{h}}+1 \\ W_{\text {out}} &=\frac{W+2 p_{w}-k_{w}}{s_{w}}+1 \end{aligned} \]

感受野（Receptive Field）

输出特征图上每个点的数值，是由输入图片上大小为\(k_h\times k_w\)的区域的元素与卷积核每个元素相乘再相加得到的，所以输入图像上\(k_h\times k_w\)区域内每个元素数值的改变，都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。感受野内每个元素数值的变动，都会影响输出点的数值变化。比如\(3\times 3\)卷积对应的感受野大小就是\(3\times 3\)。

多通道操作

实际应用中通常都是多通道进行卷积，如图像的RGB三个通道，这样的数据输入和输出都是多通道的，所以需要能够处理多通道的场景，除此之外，神经网络中多采用批训练的方式，所以卷积算子需要具有批量处理多通道的能力。

• 多输入通道场景

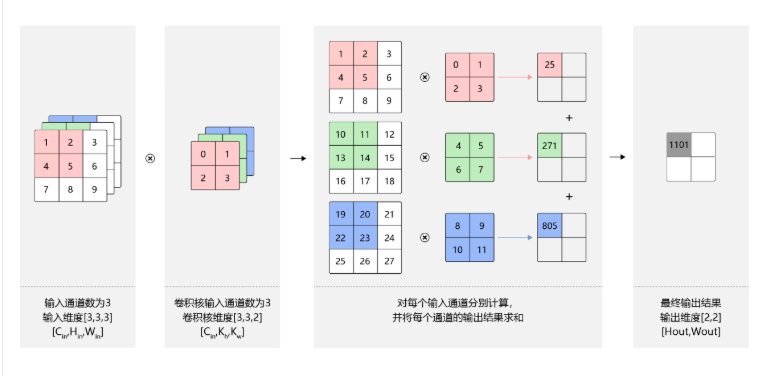
  假设图片的通道数为\(C_{in}\)，输入数据的形状为\(C_{in}\times H_{in}\times W_{in}\) ，则计算过程如下图所示：

  1. 对每一个通道分别设计一个2维数组卷积核，所以卷积核数组的形状为\(C_{in}\times k_{h}\times k_w\) 。
  2. 对任意一个通道，分别用对应通道的卷积核进行卷积运算。
  3. 将这\(C_{in}\) 个通道各自的卷积计算结果相加，得到一个形状为\(H_{out}\times W_{out}\) 的二维数组。
  4. 其中\(H_{out}\times W_{out}\) 的大小依据单通道的公式计算即可。

  

• 多输出通道场景

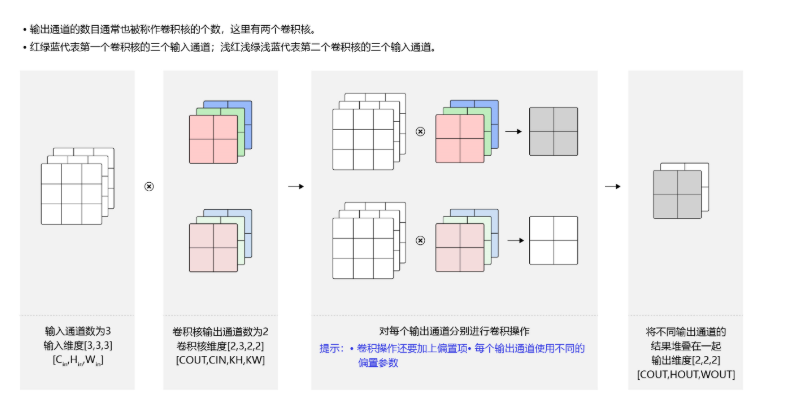
  一般来说，卷积操作的输出特征图也具有多通道\(C_{out}\) ，这时我们需要设计\(C_{out}\) 个维度为\(C_{in}\times k_h\times k_w\) 的卷积核，这里可能不太好理解，不过只要多一点点思考就可以想明白了，其实只是在维度上增加了而已，不过实际中通常我们将多通道输出个数叫做卷积核个数，因为四维空间较为抽象，卷积核数组的最终维度为\(C_{out}\times C_{in}\times k_h\times k_w\) ，如下图：

  1. 对任一输出通道\(c_{o u t} \in\left[0, C_{o u t}\right)\) ，都是使用上面描述的\(C_{in}\times k_h\times k_w\) 卷积核对图像做卷积得到的。
  2. 将\(C_{out}\)个形状为\(H_{out} \times W_{out}\) 二维数组拼在一起，就得到\(C_{out}\times H_{out}\times W_{out}\) 形状的多通道输出。
  3. 对这个的理解，需要一步步的，首先掌握单通道的卷积尺寸计算，然后掌握多输入通道场景的计算，再然后就可以很好理解多输出通道场景的计算了。

  

• 批量操作

  卷积神经网络中，通常进行多样本一起训练，即输入数据的维度为\(N\times C_{in}\times H_{in}\times W_{in}\) 。由于会对每张图片使用同样的卷积核进行卷积操作，所以卷积核的计算和上述多输出通道一样，卷积核的维度仍然是\(C_{out}\times C_{in}\times k_h\times k_w\) ，输出维度为\(N\times C_{out}\times H_{out}\times W_{out}\) ,如下图所示：

  

池化（Pooling）

简介：池化是使用某一位置的相邻输出的总体特征代替网络在该位置的输出，经过池化操作后，特征图的尺寸会变得很小，一定程度上可以减少神经元的个数，节省空间提高效率。

方法：平均池化和最大池化。平均池化即取池化窗口区域数值的平均值作为池化结果，最大池化即取池化窗口区域的最大值作为池化结果。图例如下：

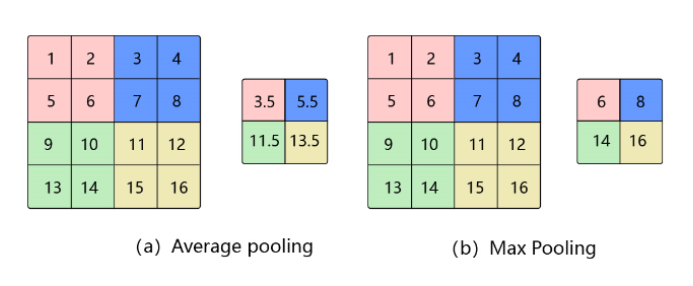
输出尺寸计算：池化层与卷积层类似，也可以进行Padding，也有步长，也有池化窗口，这里设步长为\(s_h\) 和\(s_w\) ，高度上填充为\(p_{h1}\) 和\(p_{h2}\) ，宽度上填充为\(p_{w1}\) 和\(p_{w2}\) ，则池化层输出尺寸为：

\[\begin{aligned} H_{\text {out}} &=\frac{H+p_{h 1}+p_{h 2}-k_{h}}{s_{h}}+1 \\ W_{\text {out}} &=\frac{W+p_{w 1}+p_{w 2}-k_{w}}{s_{w}}+1 \end{aligned} \]

激活函数

激活函数为神经网络提供了非线性的性质，提高了神经网络的表现能力，所以在神经网络中选择合适的激活函数是十分重要的。常用的激活函数有sigmoid、tanh、Relu、Leaky Relu、MaxOut等，目前在深度学习中Relu的效果还是较为不错的。关于激活函数更详细的介绍可以参考该博客《常用激活函数总结》 ，这里就不过多赘述（其实我就是懒了，不想造轮子总结，拿来主义也挺好，并且个人觉得这个博客讲的挺清晰明白的，希望读者谅解呀^0^）。

批归一化

模型的收敛需要稳定的数据分布，归一化（标准化）可以将数据映射到一个稳定分布的空间。对于浅层的神经网络，可能只需要对输入数据做归一化就可以得到较好的结果，但对于深度神经网络来说，仅仅对输入数据做归一化是不足够的，我们还需要对中间过程的输出数据也做归一化，从而让深度网络模型也能很好的收敛，提高模型的稳定性。详细内容

批归一化公式计算过程

1. 计算mini-batch内样本的均值

2. 计算mini-batch内样本的方差

3. 计算标准化之后的输出

4. 对标准化的输出进行平移和缩放

   如果强行限制输出层的分布是标准化的，可能会导致模型某些特征模式的丢失，所以会紧接着需要进行平移和缩放

注：如果一个样本具有多个特征，则对每个特征分别计算均值和方差

批归一化实践技巧

上面讲到的批归一化计算过程，我们是以一个batch为例的，只是为了讲清楚具体的计算公式，但我们在实际预测时候，如果是以一个batch的数据的均值和方差来归一化，则会导致同一个样本在不同的batch中归一化结果不同，导致预测结果不一致，存在偏差，这并不是我们想要的结果，所以我们需要在整个数据集上进行归一化的操作，具体如下：

1. 解决方案：训练时计算在整个数据集上的均值和方差，并将结果保存，预测时不计算样本内均值和方差，而是使用训练时保存的值

2. 计算方法：在训练过程中通过滚动平均的方式，计算在整个数据集上的均值和方差并保存，公式如下：

   \[\begin{array}{l} \text { saved } _{-}\mu_{B} \leftarrow \text { saved }_{-} \mu_{B} \times 0.9+\mu_{B} \times(1-0.9) \\ \text { saved }_{-} \sigma_{B}^{2} \leftarrow \text { saved_ } \sigma_{B}^{2} \times 0.9+\sigma_{B}^{2} \times(1-0.9) \end{array} \]

   \(saved_{-}\mu_{B}\) 表示训练过程中前面所有轮次的滚动的均值；

   \({ saved }_{-} \sigma_{B}^{2}\) 表示训练过程中前面所有轮次的滚动的方差；

   0.9表示滚动平均的动量系数（momentum)；

   \(\mu_{B}\) 表示本轮batch数据的均值；

   \(\sigma_{B}^{2}\) 表示本轮batch数据的方差；

   按照上述公式不断迭代，直到训练过程结束，最后得到的均值和方差保存下来，作为预测数据归一化的均值和方差。

注：也许你会觉得可以直接针对整个数据集计算出均值和方差并保存下来，这样确实是很直观的一个方法，我个人刚开始也是这样想的，但课程中老师并未详细解释，后续我会继续跟踪这个问题，如果您偶有所了解，非常欢迎在评论区留下您的见解！！！

丢弃（Dropout）

简介

Dropout是一种抑制过拟合的方法

方法

1. 训练阶段：每次随机的删除一部分神经元，不向前传播所携带的信息，相当于每次都是让不同的模型在学习
2. 测试阶段：向前传播所有神经元的信息，相当于让不同的模型一起工作

直观来看，如下图所示：

如果需要进一步了解Dropout的原理和实践操作，请参考该博客《Dropout原理解析》

总结

卷积神经网络基础的小结就到此结束了，非常感谢您能读到这里，也更加希望您能在看完本篇长文后有所收获，你的进步和鼓励就是我作为知识搬运工的最大动力！！！

有任何疑问都欢迎在评论区提出讨论，分享交流，共同进步！！！

参考资料

1. 百度飞浆教程