2.计算机组成-数字逻辑电路 门电路与半加器 异或运算半加器 全加器组成 全加器结构 反馈电路 振荡器 存储 D T 触发器 循环移位 计数器 寄存器 传输门电路 译码器 晶体管 sram rom 微处理 计算机
现代计算机的各个部件到底是如何通过逻辑电路构成的呢
半加器
我们说过了门电路
看似简单的三种门电路却是组成了整个逻辑电路的根基
真值表--其实就是根据输入输出状态枚举罗列出来的所有可能
比如有一台设备,他有两个输入A和B
无论何时,他们都有电或者都没有电的时候是正常,任何一个有电就是不正常
那么他的真值表就是这样子的
AB表示输入 F表示输出
第一步:找到F=1的行
第二步:把表达式写成数理逻辑的形式,如果是0写成非的形式
第三步:各个逻辑"加"起来
继续翻译成逻辑电路的话那就是
A与B的非门连接到一个与门
A的非门与B连接到一个与门
然后再把这两个连接到一个或门
符号
是不是很简单?
就好似摩天大楼由砖头(与) 水泥(或) 钢筋(非)组成一样
一块砖和另一块砖叠在一起很简单,但是组成摩天大楼就会很复杂
其实这个电路不就是一个异或门吗
a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
再回头看一下上面的真值表
A和B经过这个设备,输出为F,是不是可以这样描述
0⊕0=0
0⊕1=1
1⊕0=1
1⊕1=0
设想一下二进制的加法是什么样子的?
0+0=0
0+1=1
1+0=1
1+1=0(此处应该有进位1)
这不就是没有进位的二进制加法运算设备吗?
所以说
异或也叫半加运算
--之所以说是半,是因为他没有进位机制
全加器
想要计算加法,很显然我们需要一个全加器,就是有进位的,对吧,这是很自然的逻辑思维
百度百科中如是说:
全加器是能够计算低位进位的二进制加法电路。
是用门电路实现两个二进制数相加并求出和的组合线路.
与半加器相比
全加器不只考虑本位计算结果是否有进位,也考虑上一位对本位的进位,
可以把多个一位全加器级联后做成多位全加器.
用现在的概念去解释描绘历史,好像不是那么合适,但是我觉得会更有利于理解
全加器不只考虑本位计算结果是否有进位,也考虑上一位对本位的进位
如果不理解的话,可以拿出纸笔来计算,比如
前一个进位1 显然就是上一位对本位的进位
后一个进位1 显然就是本位计算结果是否有进位
每一次的计算,都有三个输入,加数和被加数,以及来自上一位的进位
每一次的运算,则会产生当前位的结果,以及向下一位的进位
所以一次计算会有5个变量
我们用A,B分别表示两个输入 加数和被加数
Ci表示来自前一列的进位
S是加数A被加数B以及Ci的和,和并不太准确,也就是求和后当前位的值
C0表示本位计算结果对下一位的进位
显然,A,B,Ci都可能有不同的值
我们列一下S的真值表 表示当前位计算的结果
三位的组合,每位可能两个值,所以总共8种可能
按照之前的步骤,找出来S为1的行,0用非来表示,最后求和
C0的真值表 表示当前计算结果是否有进位
也是三位的组合,每位可能两个值,所以总共8种可能
我们转换成电路
不要问我怎么画,你就按照我们上面的两条逻辑对着电路图走一遍
看看是不是这么回事就好了,反正我自己只是要理解计算机,而不是去设计电路
你要想搞得很明白,你可以去研究下
数字逻辑与数字系统设计或者数字逻辑XXX与XX设计一类的书名的书籍
我们可以把上面的式子简化下
可以简化为
我们之前已经知道对于 异或电路半加器
a⊕b = (¬a ∧ b) ∨ (a ∧¬b) 也就是a与b的异或就是

简化为
根据:
就可以得到下面的电路图
根据输入输出的变量情况
我们可以用下面的图来表示一位全加器
有了一位全加器,我们自然可以组合出来更多位的全加器
看三位的全加器有了
S3 S2 S1 S0 的排列就是计算出来的结果,不是吗
我们继续抽象一下,一个加法计算器就出来了
根据之前提到过的一些知识理论,我们可以很容易想得到
对于左侧的输入,我们完全可以根据电路的闭合和联通来确定是0 还是 1
对于右侧的输出,我们可以接上小灯泡,用亮和灭来记录结果
反馈电路 振荡器 -计算机的心跳
之前提到过,继电器的常用场景之一就是用作控制电路
如下图所示
想想我们之前的非门
带电源的常闭式(就是右侧电路默认是闭合)的继电器就是一个非门
刚已经说过,上面是用作控制电路,左侧电路控制右侧,右侧也是有电源的
如果共用电源
可以很明显的看得出来
开关本身是闭合的,一旦接通电源
吸引衔铁开关,断开电路然后失去磁性,然后电路闭合
吸引衔铁开关,断开电路然后失去磁性,然后电路闭合
.....
他是一种特殊的非门
把自身的输出结果拿过去作为输入
把一个非门的输出拿出来一部分作为它的自身的输入这叫做反馈
那也就是说一个非门加上一个反馈
就构成了这样子的一个装置,可以反复的在两种结果中跳转,并且无限持续
这就是 振荡器
能够产生一连串无限(只要有电)交替变化的输出
可以想象得到,振荡器的变化形式类似下面的形式
也就是高低交替的(不要去纠结到底是横线多长间距多大两行之间有多高~)
电流的切换速度是极快的
所以我们直接忽略时间,认为他是瞬间就可以达到,否则他肯定是斜线
上升沿:电压从0到最大值的上升的竖线叫做上升沿
下降沿:电压从最大值到0的下降的竖线叫做下降沿
触发器-记忆
然后又有两个人才研究出来了一个更加特殊的连线方式
电路上下对称,分别都是一个或门连着一个非门
他们各自的输出又分别是对方的输入
两个或非门首尾相连形成两个反馈
再次强调不要纠结这到底是啥,我相信最初肯定是瞎弄的,科学不就是尝试么
然后发现了有些有意思的地方,然后就被加深研究了
如果左侧加上电源 右侧接上两个灯泡的话
根据开关闭合与断开 以及灯泡的情况
研究出来了触发器的原理
工作状态依赖于两个开关R S
闭合一个断开另一个,总是会得到两个相反的输出Q和Q~
要是全部断开,那么取决于Q和Q~刚才是什么状态,也就是有记忆功能
最早的一种触发器,称之为R-S触发器
Q和Q~总是以相反的状态出现
0 1 或者1 0
触发器截然相反的两个输出,不过多数情况下仅仅使用一个
触发器的记忆功能被应用到计算机的存储上
使用Q来记忆一个比特,另外一个就不用了,因为本来他们就相反
要想使用Q保存一个比特,自然离不开R S
想要Q=0 S=0 且R=1
想要Q=1 S=1 且R=0
两个输入可以用非门表示
当电路刚接好(还没有按下开关),S为0 R=1 Q=0 灯泡不亮
当按下开关后,S为1 R=0 Q=1 灯泡亮了
但是一旦开关断开,灯泡立刻又灭了,因为又回到了刚才的状态
显然,虽然可以保存1比特,但是并不能维持他的存在,因为R和S作为输入发生了变化
所以很自然的,想到在R和S外加一层控制
然后又发明了带控制的触发器 D触发器
CP作为控制线路
Cp=0 时,通过与门,自然不管D上是什么,S和R都为0,触发器保持原有内容不变
CP=1 时,如果D=0 那么 S=0 R=1 Q=0
CP=1 时,如果D=1 那么 S=1 R=0 Q=1
也就是说CP作为控制线路控制是否可写
在可写的情况写,D控制写入的内容
这种触发器会在CP=1期间都可以进行写,只要D改变了,保存的值就会发生改变
所以想要准确的保存一个比特,你需要保持住D的值,持续经过CP从0~1然后再到0的过程
所以,又发明了一种新的触发器,仅仅是在CP从0变成1 或者从1变成0 的时候才会触发
-也就是接受D的输入
两个D触发器首尾相连而成,前一个触发器的输出是后一个触发器的输入
这两个触发器不会同时工作
这个触发器是上升沿D触发器
也就是不管控制端是0 还是1 还是从1到0的下降沿,都不能保存
只有0到1的上升沿才能保存
如果把若干个上升沿D触发器连接起来
最初开关是断开的,所有的触发器都不工作
因为CP都是0
如果你不停的按开关,最初闭合开关瞬间的这个比特1 就会在触发器间顺序传递,从左到右
手动按动开关自然是无聊的,所以振荡器就被应用其中了,而且速度是可调节的
这种走马灯的电路就是 循环移位寄存器
寄存,是临时存放的意思
当若干个触发器组合在一起,可以同时保存多个比特时就成为寄存器
计数器
T触发器 Q~作为输入到D
假设最初Q=1 Q~=0 灯泡是亮着的
反复按动开关(按键开关),灯泡会在亮灭之间交替变化
每当一个脉冲到达CP时,触发器的输出就会发生翻转,原先是0 则变成1 原先是1 则变成0
Q~也是这样,只不过值刚好相反
他有一个神器的作用就是用于计数
简化一下(隐藏了Q~到D的连线,但是他是存在的)
5个连接在一起,从右往左看,每个触发器的输出端Q~都连接下一个触发器的CP
先把每一个触发器清零 使得 Q43210 的值为00000,这表示0
随着振荡器脉冲的输入,会不断计数
显然,一个触发器表示一个比特,8个触发器组成计数器,就是可以累积255个脉冲 11111111
试想一下如果计数器已经达到最大了,此时又来了一个脉冲,是什么效果?这不就是溢出的基本原理么
寄存器
试想一下如果多个数通过全加器进行计算,需要解决什么问题?
之前我们说到过半加器到全加器的进化,需要记录处理进位的情况类似
多个数相加,自然需要处理中间结果,所以你需要保存下来
寄存器的符号(就是触发器组成 多个触发器可以构成寄存器)
上升沿才会工作
把加法器换一种形式描绘
如果你还记得到话,之前是这样子的
我们把寄存器连接到加法器上
你应该可以看得懂
当按键开关KRA按下时,开关输入的数值会通过寄存器,输出到加法器,作为他的一个加数
为了简化电路图,使用同一组开关提供加数和被加数
这样,通过开关送进来的数可以先到到寄存器RA ,同时也被送到加法器另一个输入端
如果你想要保存到寄存器RA就按一下按键开关
如果你想要用它和寄存器中的数相加,就什么也不用做,结果自动从加法器的输出端
所以当你输入第一个数字,按一下KRA开关,寄存器保存了加数
输入第二个数字,寄存器的值就和他相加 立刻得出结果
然而此时的寄存器还没有保存中间结果
一种很显然的方案就是加法器的输出,同寄存器的输入端直接相连接
很显然,共用电路带来了很多麻烦
比如加法器计算出来的结果不仅会达到寄存器还会进入自己的输入端
所以说要么就是想办法电路分开,要么就是轮流共用线路
大家共用的线路,就是我们常说的总线
轮流使用总线 传输门
继电器的作为控制电路的理论再次被应用
这种结构就叫做传输门---开关闭合,信号可以通过,开关断开,信号就中断
名字很形象
所以可以使用传输门来控制总线上数据的传输
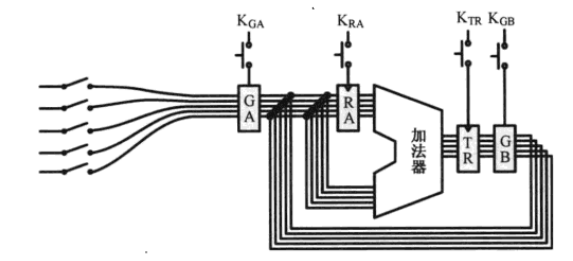
上图中都是按键开关,不是闸刀开关
左边通过传输门GA接入总线
右边加法器输出通过GB接入
而且还多了一个临时寄存器TR 临时保存加法器的计算结果
计算过程是这样子的:
比如 1+2+3+4+5
第一步:开关拨出来第一个数 ->按住KGA打开传输门->按下KRA,数据保存在寄存器RA中,松开KGA,关闭传输门
虽然此时这个数据已经也到了加法器的另一个输入,加法器也会进行运算,但是GB关闭的,TR也不会进行保存
第二步:开关拨出来第二个数
->按住KGA打开传输门,这样第二个数被加数会进入加法器的另一个输入端,加法器会自动运行
->按一下KTR,保存计算结果到临时寄存器
->松开KGA
->然后就是按住KGB,让临时寄存器TR的数据达到RA
->按一下KRA寄存器保存中间结果
虽然也会输入到加法器的另一个输入端,也会进行加法,但是TR会屏蔽掉数据不会保存
梳理简化下步骤:
按住KGA 按一下下KRA 松开KGA===>保存了加数
按住KGA===>计算结果
按一下KTR 松开KGA 按住KGB 按一下KRA===>保存中间结果
译码器
你可以去设想可能的电路,找到输入输出,然后列出真值表
然后设计逻辑电路,这是通用的解决问题的思路
比如我们设想

经过这样子一个电路,我们可以更方便的操作,图中假定设置加数 是装载 设置被加数求和 是相加
再次优化
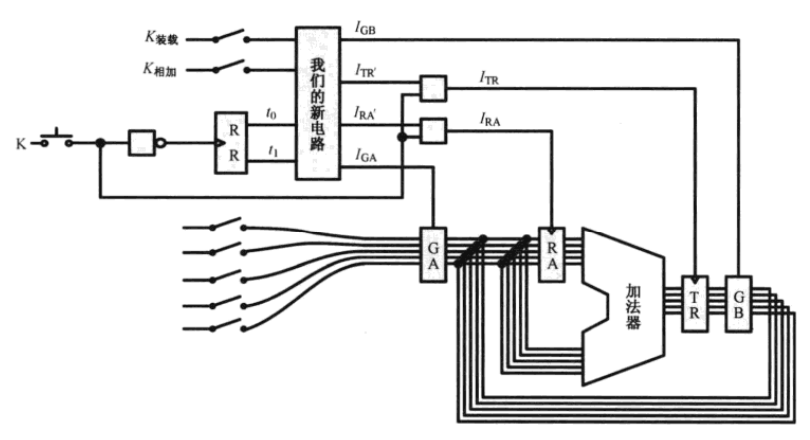
RR是循环移位寄存器,两个输出t0 t1 替代了K0 K1
这样子就是最开始的时候需要装载,此后都是开关拨数,按两次K,开关拨数按两次K..
这就是控制器的基础原型
上面的这个新电路其实就是译码器,译码器就是用于输入的转换,把一种输入转换为另外的一种输出
如同名字一样,翻译
至此,我们已经可以通过相对比较简便的操作进行连续累加
但是每次不断地拨弄开关进行数据输入,仍旧是比较繁琐的
存储器
存储器按照我们的理解,他像一个容器一样,有一个口可以进行 存 / 放 数据
之前说过想要存储数据那就是触发器-上升沿D触发器
G是传输门,控制Q与外部世界的连通性
默认W和R都为0 G是断开的
写入时,DB输入数据,W从0变成1 上升沿 R继续为0,G是断开的
读取时,R=1 打开传输门,W仍旧为0
作为一个基本单元,可以构造容量更大的存储器
使用几个就是可以保存几个比特的二进制数
默认读写均为0
D0~D4准备好数据 写从0~1上升沿,写0 写入数据
写0 读1 读取数据到D0~D4
想要保存多个二进制数,只需要垂直方向增加
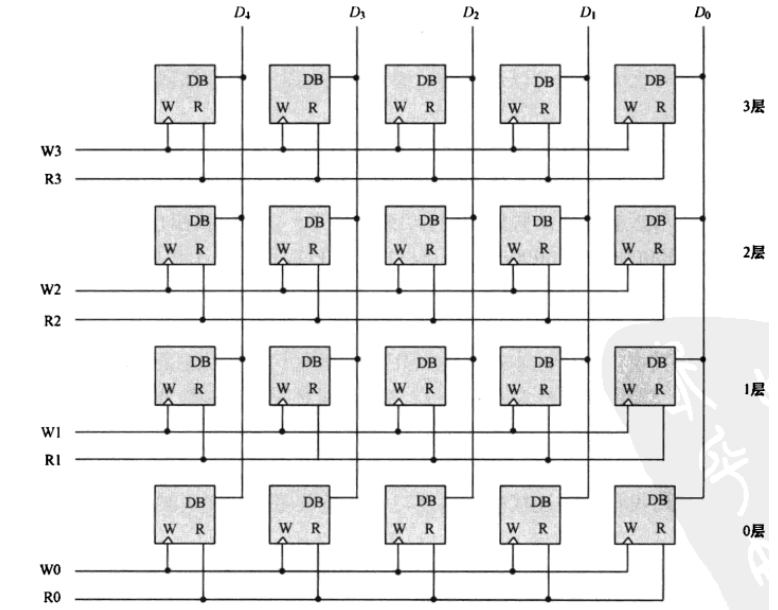
显然,随着可以保存的数据的增多,此时就面临着你到底要保存到哪里的问题
你要保存到哪里,就要控制指定的W和R的状态
地址译码器
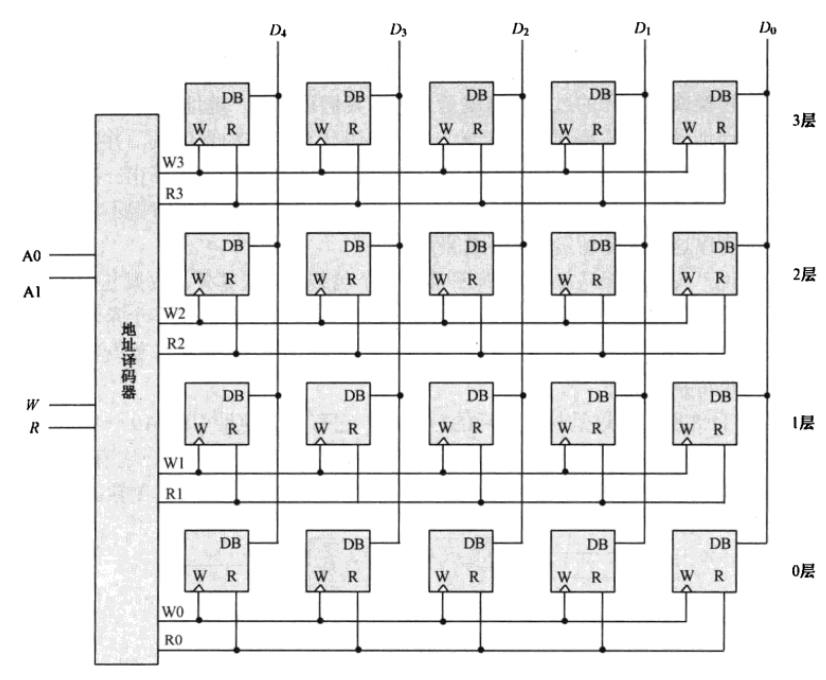
相信你完全可以理解他的逻辑,给定比如01 表示对应的W1 和R1
W和R表明读写情况
这就是地址译码器,找到具体存储单元的门牌号
简化后的存储器就是这样子的,
5个D 数据输出总线,表示这是一个可以保存5个比特的存储器
也就是一次可以读取或者写入一个5比特的二进制数
A表示寻址空间的范围 四位就是0000~1111 16个单元
磁芯存储器
磁芯是容易被磁化的东西一个圆环,磁芯中穿过一根电线
根据电磁学的原理,电流方向不同,磁化后的南北两极是相反的
磁场又可以反过来产生电流
也就是说可以把一个状态看做0 一个状态看做1
这样就可以通过这跟驱动线写入数据
写入数据比较简单
读取还需要穿另一根线,读取线
静止的导体不会发生什么变化
所以读出数据时,用驱动线写入 0
如果本来就是0 不会有太大变化,读取线上电流很小
如果本来是1 磁场发生变化,直接翻转,那么读取线电流会比较强烈,表示读出是1
但是显然具有破坏性,所以如果读出来的是1 需要重新写入1
和触发器不同,磁芯存储器断电之后仍旧能够维持写入的数据
有了存储器就可以从存储器中读取数据,然后进行累加运算
一种很自然的方式就是这样子的
其中我们假定,数据连续存放
从0000 开始 存放五个数比如 1+2+3+4+5
AC最初是0000 每按一次Kac地址加1 进行读取下一个地址
AR是寄存器,临时存放存储器的地址
Krd用来控制读取
数据寄存器DR暂存读取的数据
这样就完成了从存储器顺序读取的功能
初始时AC为0
按一下KAR AC写入地址寄存器,提供给存储器
按住KRD,在按一下KDR,数据被DR保存,最后松开KRD
再按一下KAC 地址计数器指向下一个地址
又遇到优化电路的事情了,我们可以根据之前的译码器 再次简化
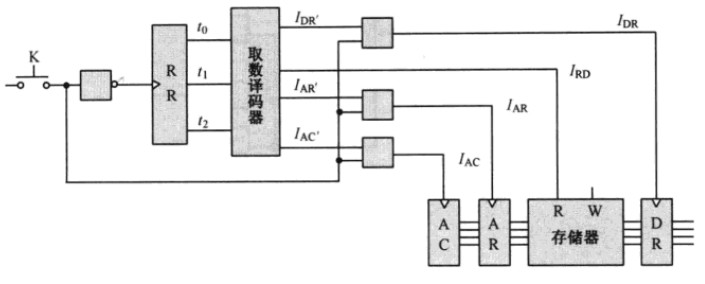
此时仅仅需要一个按键开关即可控制连续取数
将存储器 译码器加法器连接起来就是下面的样子
可以通过三个按键的配合进行半自动的结果计算

如何才能更加优化上面的电路
这就需要用到指令的概念,因为相加 装载本身就是一种命令
一种命令自然对应着 固定的执行路径
所有的指令都有一个操作码开始指示出指令的功能
比如装载,表示下一个存储单元是需要装载的数据,目标是寄存器RA
相加表示,第一个加数位于寄存器RA 第二个加数位于下一个存储单元,最终结果保存到RA
有了指令的概念模型,我们就可以把指令和数据融入到一起,指令本身也是二进制数据
一条完整的指令总是以操作码开始
有的指令可能不需要操作数,只有操作吗即可
有的可能需要不止一个操作数
这就出现了一个新的问题,那就是译码,翻译操作码
简洁高效的翻译出操作码,就可以替代装载和相加指令了不是么
而且也应该想得到,如果行得通,还可以表达更多的指令
再次使用译码器来模拟开关,使用一个开关开控制将所有的数据从存储器依次取出
并且逐个相加
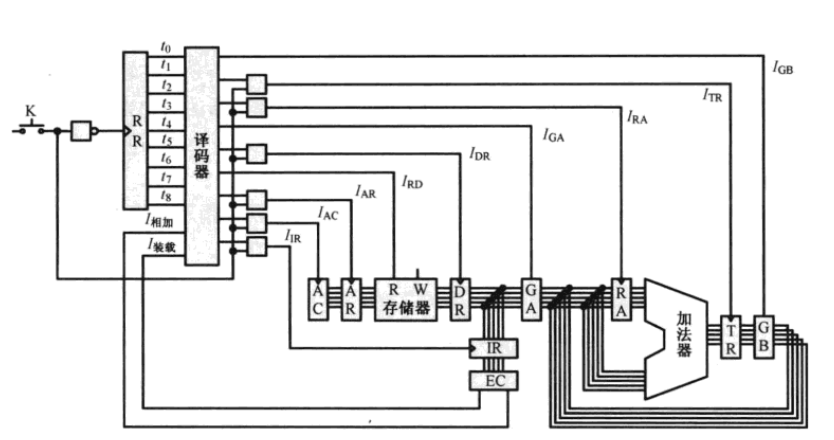
循环移位寄存器,向走马灯一样,将会呈现出周期性
0~2阶段 取指令 地址计数器AC自动加1 取指令阶段
第一个操作码位于DR中
3阶段 IR地址寄存器将操作码保存起来 IR输出直接指向译码电路EC,解析操作码 指令译码阶段
4~8依次执行下面的任务
从下一个存储单元里取数,地址计数器AC加一,把取出来的数装载到寄存器RA中
至此第一条指令执行结束,循环移位寄存器也已经经过一次完整循环(假定第一条指令是装载 也就是加载 加数)
第二个也是0~2取指令3 译码 4~8取数数据与RA相加
至此想要五个数相加怎么办?
编写5条指令,按动9次开关(0~8)
还是有点麻烦
其实反复按动开关,不就是振荡器的工作原理么
不过你要知道,你需要严格控制,什么时候振荡器停止,也就是不在一直按开关
所以需要增加一个新的指令 停机指令
放到所有你想要执行的指令的后面,当然你需要重新设计译码电路EC

现在我们的自动加法器已经具备了以下元素:
存储器 运算器 控制器 驱动控制器的振荡器
SRAM/DRAM/ROM
晶体管来做大容量的存储器也变为现实(此处不是说超大规模集成电路时代才可以)
晶体管可以构建触发器,触发器又可以形成大容量的存储器
这就是静态存储器SRAM Static Random Access Memory
不过使用触发器构建存储器需要集成很多晶体管
后来又发现,要想存储一个比特,只用一个晶体管和一个电容就可以
最早的电容器 是18世纪发明的莱顿瓶
电容的特点:
那就是把它接到电源上,一个金属板的电子会被拉倒另一个金属板上
电源撤走,两块金属板会保持着一块电子多余,一块电子缺乏的状态,以至于他们之间产生了电压,看起来就是储存了电
不过他会通过两极间的空气或者其他介质放电
只用一个晶体管和一个电容应用到存储器上的话,因为会泄露,所以要定时重写
这就是刷新,所以这种叫做动态存储器 DRAM Dynamic Random Access Memory
除了RAM还有ROM, Read Only Memory,也就是只能读取
只读存储器最大的优势在于可以一直维持所保存的内容,即使断电
再后来又发展出来 可编程只读存储器 再后来 可擦除可编程只读存储器
我们知道逻辑电路可以根据不同的输入产生不同的输出
我们知道这些输出是固定的组合,是有限的序列
那我们是不是可以把这些结果全部都枚举出来?
也就是数学上经常用到的查表法,就好像你不记得乘法口诀,你拿到两个数去乘法表中查找
ROM一个颠覆性的作用就是可以作为这种查表法的媒介,只不过他代表的是逻辑电路的运算
他的好处很显然,逻辑电路一旦组成就没办法改变,但是ROM可以按照需要进行改写~
也就是一定程度上完成了硬件的改变,不是么
微处理器
再后来随着工艺的进步,进一步的把 运算器 控制器集成在一起
就成了芯片,也就是微处理器
也叫作CPU 中央处理单元
微处理器都需要存储器以及其他辅助设备才能工作
需要向外部提供一些地址引线和数据引线,还有一些控制信号线
他需要从外部获得电源能量
需要外部引入时钟信号(振荡器)
微处理器的另个特点是有各自的指令集
随着技术的发展,振荡器的时钟频率也来越快,也侧面反映了处理器的速度
处理器所执行的工作是大致固定的,取指令 译码 读写操作数 运算等
中间涉及到数据的传输
当处理器的处理速度高于数据的传输速度的时候
或者说并不是每一个时钟周期内处理器都在干活,可能在等待数据
处理器的性能就被拉低了
SRAM最快,但是成本高
DRAM由于要刷新,而且刷新时无法读取数据所以慢了一些
但是DRAM高密度低成本
高速缓存
可以使用SRAM作为缓存,也就是处理器和内存的一个中间地带
也即是常说的cache
不过你要尽可能的保障你想要的数据会存在cache中,这称为命中
如果不能命中还是去再次的加载高速缓存,速度很差
流水线
假设说需要两个步骤完成输出
如果每个步骤需要1个单位的时间 那么将会需要2个单位的总时间
在第一个步骤结束之后,其实他还是被占用的,直到2个周期结束后才能释放
增加寄存器就可以解决这个问题
在第一个步骤结束后计算结果保存到中间寄存器,然后进行第二个步骤
那么第一个步骤可以用来进行新的计算
这就是流水线式的处理逻辑
但是流水线式也有他自身的问题
比如跳转指令,开始执行的时候后面两条指令已经进入了流水线,这种情况,只能清空流水线
解决办法是增加分支预测功能
计算机同外部的接口
为了使外部设备和计算机核心之间进行数据传送,需要连线,也就是构造逻辑电路
在逻辑电路里面会有一些寄存器,通常叫做I/O端口,或者直接叫做端口
端口作为计算机核心与外部设备的中间人
大家都把数据放到端口上,无外乎是谁放谁取(存储/读取)
端口是交流的窗口,计算机可能有很多不同的输入输出设备,你总不能轮流使用
所以端口需要有多个,至于每个端口怎么用,跟计算机本身没有关系
外部设备决定了怎么使用这些端口
在处理器上运行的软件,决定了如何解释端口上的数据
也就是说,设备的物理输入和运行指令的逻辑解释是对应的
计算机只负责读取执行,并不关注到底是什么
如果没有与外部设备对应的软件,就没办法解释使用这些数据
计算机同外部交互,只能识别二进制
需要将模拟信号转换为数字信号
比如对着话筒讲话,或者播放音乐时,产生强弱随时间变化的电流
这时候就需要模拟-数字的转换,也就是采样
如果一秒钟仅仅观察2次或者10次,得到2个或者10个二进制数,可能会丢失很多数据
所以现在的标准而言,高品质是44.1kHz 也就是44100次/秒
计算机数据的输出,又需要转换为模拟信号
可以将端口的地址并入内存地址空间,就好像门牌号分段
比如小于100的是内存地址编号大于100的就是端口号
更好的方式是使用专门的指令进行I/O端口的访问
不同的外部设备通常有不同的接口方式,可以理解为插头的样式,这是厂家决定的
不过很多东西也慢慢地都是有标准规范的
另外就是说插头里面的信号,比如话筒的是快速变化的声音电流
所以要有这么一个东西:
可以保留已有的外部设备插头规格,也即是适配现有的
然后还需要能够进行模拟数字信号的转换
但是有一些设备还需要做一些额外的处理,计算机又不懂得,只是提供统一的端口
这些额外的处理由被称为扩展卡的部件实现比如网卡 声卡 视频卡
简易图就是这样子
简言之就是计算机同外部设备进行交互需要端口
端口需要与外部设备进行通信
进行通信就需要与原有插头连接并且进行信号转换
另外还可能需要多一些额外的处理,计算机并不懂得这些额外的处理,也就是比如声卡 网卡的功能
后来发现有些东西是大家都需要的,比如鼠标键盘显示器,所以干脆就直接集成了这些东西
也就是通过这些接口比如HDMI,计算机可以进行更多的数据处理
每一个接口功能复杂一些的一般也都有自己的微处理器
比如声卡,可以与麦克风与扬声器进行通信
声卡微处理器需要执行自己的指令,指令固化到只读存储器了
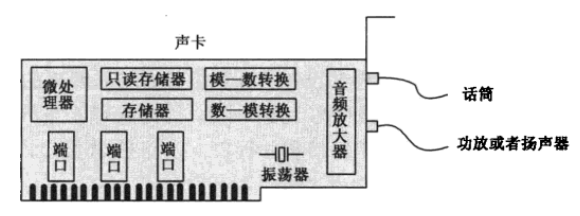
这就有一个问题,当声卡开始工作,比如录音时,二进制数据放到约定的端口上
那么在这中间,处理器将一直读取数据,也就没办法做其他的事情了
为了充分发挥处理器的性能,设计了中断
也就是可以暂停手上的工作,进行其他的工作
这是一项很好的设计,否则处理器只能串行的工作效率将是极低的
为此需要设计中断相关的线路,传送中断信号
每个外部设备有不同的中断号,一旦有了中断,计算机就可以同时处理多个程序了
有了中断,还需要有 保护现场的能力 以及 返回的能力中断返回指令
否则之前的工作不就丢弃了么
DMA
但是数据经过端口到寄存器到内存再到中央处理器内部,数据的传输是很慢的
所以不能一点点的传输,这就又用到了缓存的概念
声卡可以有自己的本地存储器,到了一定时候,启动一个存储器到存储器之间的高速直接传送
称为直接存取 Direct Memory Access
键盘
键盘的原理也是类似的,他也并不是直接接到CPU上,也是通过"键盘控制器"功能同声卡的东西
与端口进行数据交换
cpu并不认识键盘的
键盘有自己的微处理器,通过线路,他知道到底是哪个键被按下
键盘被按下,传送数据到中央处理器
到底应该传送什么数据呢?
其实他发送的是代表这个按键的二进制代码
为了使用同一种编码在不同的计算机设备间传输数据,1967年出台的ASCII
就是现在键盘使用的一种编码方式
ps;二进制数是串行的方式的传输的,一个比特一个比特送到主板上的键盘的IO接口
当然,到底如何解读这个键盘的输入,取决于当前运行的软件



 浙公网安备 33010602011771号
浙公网安备 33010602011771号