最近公共祖先(LCA)——倍增经典例题

目录

• 问题引入
• 解决过程
• 小小总结

问题引入

题目来源于洛谷P3379，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先

解决过程

经典的多种思路一览（军火展示，bushi）

• 路径交叉的第一个点就是LCA，记录各点的父亲结点，不用跳点，直属即可，然后从两点开始向根节点出发，第一个点经过的点全部标记为true，第二个点经过的第一个true点就是最近LCA，时间复杂度就是O(n)
• 没有倍增的“倍增”用法，也是只记录一级父亲节点，在遍历的时候记录每个点的深度，首先将两个点'提到同一高度'，然后一直向上跳，直到两点相同，时间复杂度也是O(n)，其实关于我说它是倍增的“倍增”用法也是有原因的对吧，这个时间复杂度主要就在于提点和跳点两个步骤，也就是这两个步骤可以优化
• 倍增用法，和第二种方法的不同在于fa的记录和跳点的方法，准确来说，是只有跳点的方法不同，所以导致了fa的记录不同，这里fa开二维数组fa[i][j]指的是第i个结点的第2^j个父亲结点，比如fa[i][0]就是直属父亲结点，下面简单介绍一下倍增里面的几个核心操作
  1. fa[][]数组的记录
     不对，虽然fa[][]的遍历是先进行的操作，但是我的认知就是他是跳点原理的“果”，建议先看下面的跳点再看这里的数组预处理操作
  2. 跳点的原理
     求LCA的操作中存在两次跳点操作，一次是提点，一次是跳点；这两次操作略有差别，第一次跳点是可知的高度跳，第二次就是不可知高度，这里给出我认为的跳点的核心原理，二进制数的转化+加法交换律+逼近法。第一次可知高度的提高就是纯纯用了二进制的规律，即对于任何一个数，都可以把它拆解成2⁰+2¹+...+2ⁿ的形式，也就是说，任何一个高度，都可以通过2的次方拆解，因此我们对于每一个高度，就相应的跳其二进制位上为1的位置即可，这里就直接给出代码：

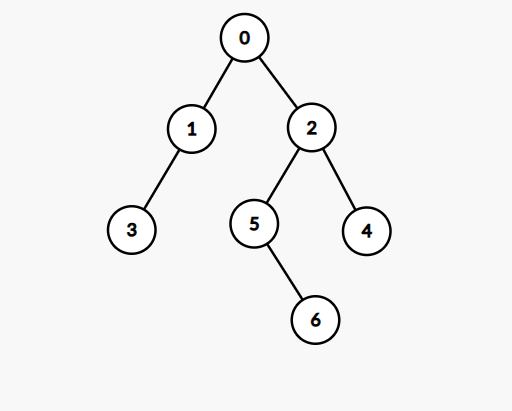
     //找的是x和y的LCA，将更深的点换成x，便于统一处理
     int z = dep[x] - dep[y];
     for(int i=0; z; i++, z/=2) {
         if(z&1) x = fa[x][i];
     }
     

     第二次跳点就比较抽象了，同时这里也是我说还有加法交换律存在的原因，如下图所示(这里插一句，大家有没有什么好用的画图软件，球球了)，我们求3和6的LCA，首先6被提到5，假如我们这时一步一步向上，那么时间复杂度还会使O(n)，但是我们要正向跳的话又不知道i最大可以取多少，因此我们采用逆向跳，其实将十进制数转为二进制数的方法中应该也有这一种方法，也就是找到小于该数的第一个2的次方数，然后继续向下找，直到1，我们这里也是一样，从最高的位置开始，假如他们的高位祖先相同，则代表这一个节点至少是公共祖先及以上，假如这个时候我们向上跳的话之后就不好分辨，因此继续，直到第一个不相同公共祖先的出现，我们就变化，最后x和y的位置就是LCA的子节点位置，按照该图来看就是x=1， y=2，最后向上提一步就可以了
     
     下面是大致的代码展示部分

     for(int i=20; i; i--) {
         if(fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
     }
     //最后一步，也是因为这一步，所以要把之前就调好的点分开讨论，否则这里还会画蛇添足
     x = fa[x][0], y = fa[y][0];
     

小小总结

挺抽象的，做这个题的时候有几个困惑我的点，导致我做这个题的时候磕磕绊绊的，下面一一叙说一遍，防止以后继续踩坑

1. 树的构建
   对的，我竟然因为这棵树到底长什么样准确来说是对输入迷糊了很久，（对于第一行的三个数输入，我直接主观印象就是几个点，几条边，几次询问）第一点我甚至在想有几条边，现在想到，谢谢，又被自己蠢到了，emmm，然后迷惑操作来了，由于洛谷下面的提示是给了树形结构的，所以后面的输入我都是直接按照子节点——父结点的顺序读入的，后面跑了一边暴力一分没有，这个时候我开始看到题目给我的根节点，还骂了一句，什么nt题，给这个有毛线用（对不起出题人，是我说话太早了），简而言之就是后面还迷糊了好一会才把树正确的建起来，其实这个就是做题的惯性思维作祟了，主要就是之前的很多题就是子节点——父结点这样的样式输入，导致这题还是以为这样输入，评价为，题目见少了导致的，请记住，给你根节点，就是给你dfs遍历用的，谢谢
2. 倍增的理解
   为什么我会把倍增硬生生做成暴力，我也在思考这个问题，虽然当时我写的时候已经知道做的不是倍增，但是我的脑子告诉我，你就是这样写的，谢谢，脑子保质期差不多了总的说来，我对根节点遍历之后，大致跑了两个数组，一个是深度dep[]，一个是父亲fa[][]，问题就在于这个fa数组，他没有倍增，没有！我当时跑的时候是这样记录的fa[i][j]，为i结点向上数的第j个父亲，对的是第j个，我当时心理还在想，差不多，按照最小的二叉树来说，2ⁿ已经很大了，但是我怎么没想到这可能不是满的呢，退化成链岂不是只能记录几十个节点，诶......
3. 数组越界
   这个更是重量即，在我终于清楚了fa里面是怎么存放的时候，以及怎么跳跃高度的时候，丫的一个数组越界差点给我整破防了，导致我晚上直接摆烂（bushi），早上起来看的时候才看出来，
   这里放一下罪恶根源

//注意这里的20
int n, m, x, y, rt, fa[N][20], dep[N];
for(int i=0; z; i++, z/=2) if(z&1) x = fa[x][i];
if(x != y) {
    for(int i=20; i>=0; i--) {
        if(fa[x][i] != fa[y][i]) {
            x = fa[x][i], y = fa[y][i];
        }
    }
    x = fa[x][0], y = fa[y][0];
}

早上调试的时候我还把跳跃的时候的打印出来，好家伙，一看在i=20的时候就跳跃了，直接给我整傻了，然后仔细一想，好像越界了，随机数emmm，后面把数组开大一点就好了
4. 最最最后，Code部分