关于SVM的阅读报告
关于SVM的阅读报告
组员:曾文丽 杨顼 倪元元
2020-03-12
在paper的题目中看到一个关键词——SVM,由于不清楚SVM是什么。寻得两篇博文:
http://www.blogjava.net/zhenandaci/category/31868.html
https://blog.csdn.net/baidu_36557924/article/details/79517365
本文中的文字、图片、公式全部来自于两位博主。拜读之后整理了一些(不知道对不对的)理解:
SVM要解决的问题是,找到具有最大分类间隔的最优决策面。核函数和松弛因子都是解决样本线性不可分问题的方法。惩罚因子越大,表示越重视离群点带来的损失,最优分类器也就越容易受少数点控制。可以通过对不同样本使用不同的惩罚因子来处理数据集偏斜的问题。
1. SVM是什么
SVM的全称是Support Vector Machine,即支持向量机,主要用于解决模式识别领域中的数据分类问题,属于有监督学习算法的一种。
2. SVM要解决什么问题
SVM要解决的问题可以用一个经典的二分类问题加以描述。顺便了解一些相关的名词,为了方便阅读,一些名词被设置称粗体了。
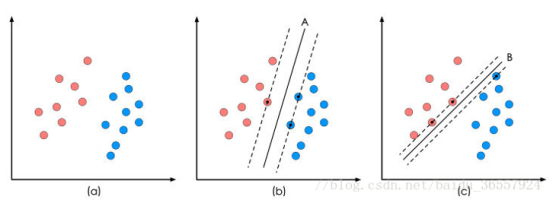
图 1 二分类问题描述
图1(a)展示了一个二维坐标、一些二维数据点(样本)在该坐标中的位置,颜色用于区分数据点(样本)的类别。
这些数据点可以被一条直线A分开,如图1(b),直线A就是一个分类函数。一般的,如果一个线性函数能将样本(数据)完全的分开,就称这些数据(样本)是线性可分的。
线性函数在一维空间里就是一个点,在二维空间就是一条直线,三维空间里就是一个平面,可以如此想象下去,如果不关注空间的维数,这种线性函数还有一个统一的名称——超平面。
将两类数据点分开的直线不止一条,如图1(c)所示,直线B也能将数据点完全分开。直线A和直线B也叫做决策面。每个决策面对应了一个线性分类器。如图1所示,这两个分类器都能将数据分开,但如果考虑潜在的其它数据,则两者的分类性能是有差别的。
图1中的数据都是准确已知的数据(先验知识),因此该算法属于有监督学习算法。分类器在样本数据上的分类结果与真实结果(样本是已经标注过的数据,是准确的数据)之间的差值,叫做经验风险。以前的机器学习方法都把经验风险最小化作为目标,但后来发现很多分类函数能够在样本集上轻易达到100%的正确率,在真实分类时却一塌糊涂(即所谓的推广能力差,或泛化能力差)。
SVM算法认为图1中分类器A在性能上优于分类器B,其依据是A的分类间隔比B要大。在保证决策面方向不变且不会出现错分样本的情况下移动决策面,会在原来的决策面两侧找到两个极限位置(越过该位置就会产生错分现象),如虚线所示。虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。虚线穿过的样本点在坐标轴中对应的向量就叫做支持向量。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。
SVM要寻找的最优解就是那个具有最大“分类间隔”的最优决策面。
3. 描述问题——建模
最优化问题通常有两个最基本的因素,目标函数和约束条件。这里的目标函数的值表示分类间隔的最大值,约束条件是对应的决策面能将样本完全分开。
接下来需要用数学语言描述该问题。
3.1决策面方程
暂时只考虑二维空间中的最优线性分类器问题,决策面是一条直线,该直线的方程形式为公式(3.1)。
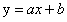 (3.1)
(3.1)
用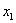 代替
代替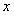 ,用
,用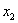 代替
代替 ,于是有公式(3.3)。
,于是有公式(3.3)。
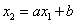 (3.2)
(3.2)
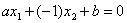 (3.3)
(3.3)
公式(3.1)的向量形式可写成公式(3.4)。
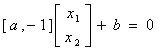 (3.4)
(3.4)
公式(3.5)是一个更加一般的向量表达形式。
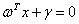 (3.5)
(3.5)
向量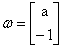 ,与直线
,与直线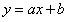 垂直。也就是说向量
垂直。也就是说向量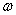 控制了直线(决策面)的方向。另外
控制了直线(决策面)的方向。另外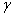 控制了直线的位置。注意在n维空间中n-1维的超平面的方程形式也是公式(3.5)的样子。
控制了直线的位置。注意在n维空间中n-1维的超平面的方程形式也是公式(3.5)的样子。
3.2分类间隔

图 2 分类间隔计算
分类间隔W是支持向量样本点到决策面的距离d的2倍,追求W的最大化也就是追求d的最大化,看起来最优化问题的目标函数已经被找到了。计算d就是计算点到直线的距离,点到直线距离的公式如下:
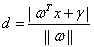 (3.6)
(3.6)
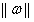 叫做向量
叫做向量 的范数,范数是对向量长度的一种度量。常说的向量长度其实指的是它的2-范数,范数最一般的表示形式为p-范数。
的范数,范数是对向量长度的一种度量。常说的向量长度其实指的是它的2-范数,范数最一般的表示形式为p-范数。
向量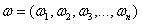 的p-范数为
的p-范数为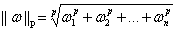 。
。
3.3约束条件
约束条件1:直线能够将所有的样本点都正确分类。
约束条件2:决策面必须在间隔区域的中轴线上,也就是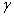 不能自由的优化。
不能自由的优化。
约束条件3:公式(3.6)中的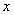 不是随随便便的一个样本点,而是支持向量样本点。
不是随随便便的一个样本点,而是支持向量样本点。
接下来用数学语言对3条约束条件进行描述。虽然有3条约束条件,但SVM算法通过一些巧妙的技巧,将这三条约束条件融合在了一个不等式里面。
先对图2中的每个样本点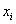 加上一个类别标签
加上一个类别标签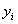 :
:
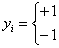
 (3.7)
(3.7)
将决策面两侧的点的值带入决策面方程会产生不同的结果:
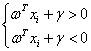
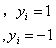 (3.8)
(3.8)
当决策面正好处于间隔区域的中轴线上时:
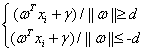
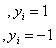 (3.9)
(3.9)
对公式(3.9)中的两个不等式的左右同时除以d,得到公式(3.10):
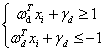
 (3.10)
(3.10)
其中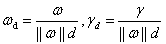 。
。
直线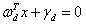 和直线
和直线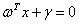 其实是同一条直线,因此约束条件可表示为:
其实是同一条直线,因此约束条件可表示为:

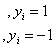 (3.11)
(3.11)
公式(3.11)就是SVM优化问题的约束条件。
3.4简化目标函数和约束条件
当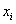 是决策面
是决策面 所对应的支持向量样本点时,公式(3.11)中等式
所对应的支持向量样本点时,公式(3.11)中等式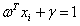 或者等式
或者等式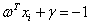 成立。所以对于这些支持向量样本点有:
成立。所以对于这些支持向量样本点有:
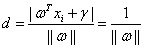 ,
,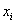 是支持向量样本点 (3.12)
是支持向量样本点 (3.12)
d本来就是支持向量样本点到决策面的距离,将支持向量带入公式(3.6)发现分子为1。因此目标函数成了公式(3.12)。追求分类间隔d的最大值就成了追求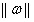 的最小值,也等效于追求
的最小值,也等效于追求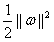 的最小值。
的最小值。
另外将公式(3.11)中的类别标签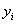 和两个不等式的左边相乘,得到:
和两个不等式的左边相乘,得到:
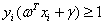 ,
,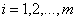 (3.13)
(3.13)
其中m代表样本点的总个数。
最终,线性SVM最优化问题的数学描述为:
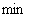

s.t. 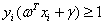
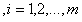 (3.14)
(3.14)
在这个问题中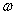 是自变量,目标函数是
是自变量,目标函数是 的二次函数,所有不等式约束条件都是
的二次函数,所有不等式约束条件都是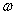 的线性函数。需要注意
的线性函数。需要注意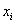 代表样本,而不是变量。
代表样本,而不是变量。
文章[2]介绍了如何把不等式约束问题转化为只带等式约束的问题。进而可以求解该问题。
4. 核函数
之前一直讨论的是线性分类器,线性分类器只能处理线性可分的样本。如果样本线性不可分,线性分类器的求解程序就会无限循环,永远也解不出来。图3是样本线性不可分的例子。
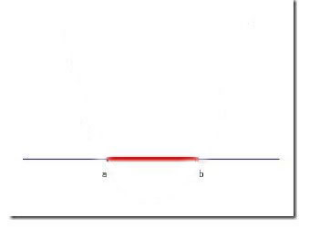
图 3 样本线性不可分的例子
图3中的样本在二维空间中,二维空间中的线性函数是一条直线,无法找到一条直线将红色线段和黑色线段完全分开。
在二维空间中,可找到很多曲线将图3中的样本完全分开。图4展示了其中一条。
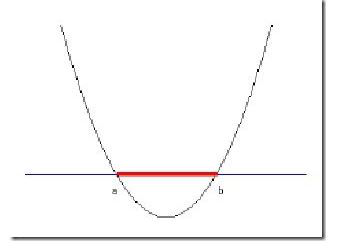
图 4 二维空间中将线性不可分的样本完全分开的曲线
曲线的函数表达式为:
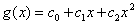 (4.1)
(4.1)
新建向量y和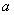 :
:
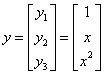 ,
,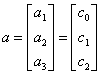
于是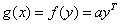 。
。 是四维空间中的线性函数。
是四维空间中的线性函数。
原来在二维空间中的一个线性不可分的问题,映射到四维空间后,变成线性可分的了。
分类过程是,先输入一个一维的向量x,将x变换为三维的向量y,然后求这个变换后的向量y与向量a的内积,将结果与阈值比较得出分类结果。图5构建了坐标系,确定了四维空间中一个线性函数的具体表达式,并进行了分类尝试。
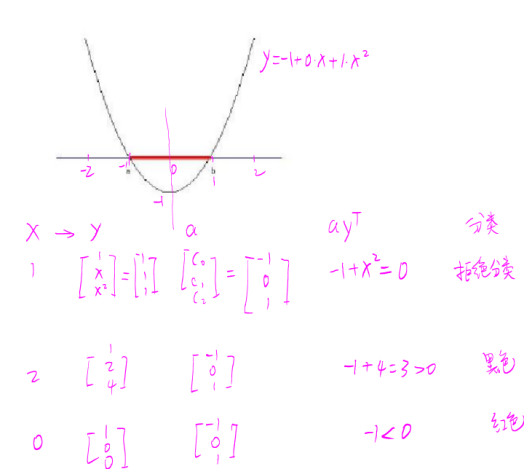
图 5 分类尝试
我们关心高维空间中线性函数的输出结果,并不在意x到y的映射关系。
核函数接收低维空间的输入值,却能计算出高维空间中线性函数的输出结果。
核函数不止一个,对核函数的选择,还缺乏指导原则。
使用核函数向高维空间映射后,问题仍然可能是线性不可分的。
5. 松弛变量
把一个本来线性不可分的问题,通过映射到高维空间而变成线性可分的,决策面的方向、位置可能如图6所示。
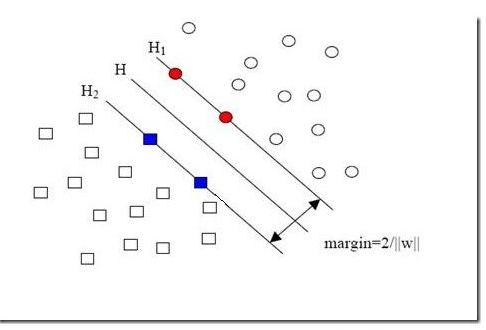
图 6 高维空间中线性可分问题
新加入的样本点可能在如图7所示黄色方块的位置。
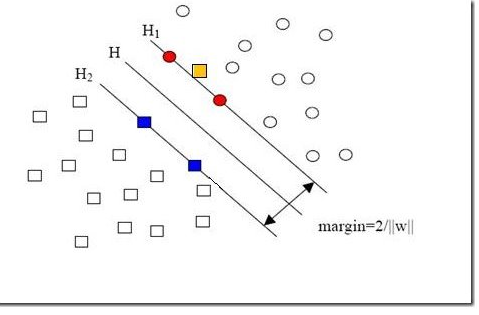
图 7 新加入的样本点
新加入的一个样本使得原本线性可分的问题变成了线性不可分。这样类似的问题(仅有少数点线性不可分)叫做“近似线性可分”的问题。
要求所有样本点都满足和分类平面间的距离必须大于某个值的解法叫做“硬间隔”分类法,其结果容易受少数点的控制。像图7这种有噪声的情况甚至会使整个问题无解。
解决方法是允许一些点到决策面的距离不满足原先的要求。
公式(3.9)可写成:
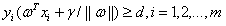 (5.1)
(5.1)
公式(5.1)的意思是说每个样本点到决策面的距离要大于d。如果要引入容错性,就给d加上一个松弛变量。
于是约束条件公式(3.14)就变成:
s.t. 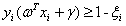
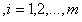
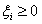 (5.2)
(5.2)
这种间隔比d小的点也叫做离群点,放弃这些点对分类器来说是种损失。但也使分类面不必向这些点的方向移动,因而可以得到更大的分类间隔。
引入松弛变量给目标函数带来了损失,有两种衡量损失的方式,使用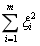 来衡量损失的分类器叫做二阶软间隔分类器,使用
来衡量损失的分类器叫做二阶软间隔分类器,使用 来衡量损失的分类器叫做一阶软间隔分类器。把损失加入到目标函数时,需要一个惩罚因子C。原来的优化问题就变成了下面这样:
来衡量损失的分类器叫做一阶软间隔分类器。把损失加入到目标函数时,需要一个惩罚因子C。原来的优化问题就变成了下面这样:
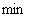
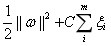
s.t. 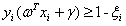
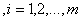
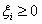 (5.3)
(5.3)
需要注意几点:
1)并非所有点都有一个松弛变量与其对应。实际上只有“离群点”才有。
2)松弛变量的值实际上标示了对应的点到底离群有多远,值越大,点就越远。
3)惩罚因子C决定了你有多重视离群点带来的损失。
4)惩罚因子C不是一个变量,C是一个必须事先指定的值。指定这个值之后,解一下,得到一个分类器,然后用测试数据看看结果怎么样,如果不够好,换一个C值,再解一次优化问题,得到另一个分类器,再看看效果,如此就是一个参数寻优的过程。
核函数和松弛变量都是解决线性不可分问题的方法。以文本分类为例,在原始低维空间种,样本相当不可分,此时用核函数向高维空间映射一下,结果仍然可能不可分,但比原始空间里的要更加接近线性可分的状态(也就是近似线性可分的状态),此时再用松弛变量处理那些少数离群点,就简单有效得多了。
6. 数据集偏斜
数据集偏斜是指参与分类的两个类别样本数量差异很大,比如正类有10000个样本,而父类只有100个。这种现象使得数量多的正类可以把决策面向负类的方向“推”,因而影响结果的准确性。

图 8 数据集偏斜
如图8所示,没提供图中两个灰色的方形点时,决策面为H;提供这两个灰色方形点时,决策面为H’。
解决方法是给样本数量少的负类更大的惩罚因子,表示我们重视这部分样本。因此目标函数中因松弛变量而损失的部分就变成了:
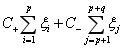
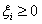
其中i=1...p都是正样本,j=p+1...p+q都是负样本。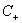 和
和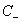 的大小是试出来的。根据具体分类问题,可参考两类样本数的比例或两类样本占据体积的比例确定出
的大小是试出来的。根据具体分类问题,可参考两类样本数的比例或两类样本占据体积的比例确定出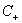 和
和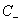 的比值。
的比值。
7. 参考文献
[1] http://www.blogjava.net/zhenandaci/category/31868.html,2009
[2] https://blog.csdn.net/baidu_36557924/article/details/79517365,2018


 浙公网安备 33010602011771号
浙公网安备 33010602011771号