GNN相关基础知识
拉普拉斯矩阵
1.拉普拉斯算子
定义为函数的二阶导数之和,即\(\Delta f = \nabla^2 f = \sum_{i=1}^{n} \frac{\partial^2 f}{\partial x_i^2}\)
根据推导可近似为\(\sum_{(k,l)\in neighbor}(f(k,l)-f(i,j))\),即邻居与点的差之和。
2.拉普拉斯矩阵
符号定义:
图上的点向量为\(V\),其中\(V_i\)表示点\(i\)的权重
图的邻接矩阵\(W\),其中\(W_{i,j}\)表示点\(i\)到点\(j\)的边权,其中\(W{i,i}=0\)。如果是无向图则\(W_{i,j}=W_{j,i}\)。如果图无边权则\(W_{i,j}=1\)
图的加权度数矩阵\(D\),其中\(d_i=d_{i,i}=\sum_j W_{i,j}\),如果图无边权则\(D_{i,i}\)就是点\(i\)的度数
则点\(i\)的拉普拉斯算子\(\Delta V_i=\sum_{j \in neighbor_i}W_{i,j}(V_i-V_j)=\sum_{j \in V}W_{i,j}V_i-W_{i,j}V_j=\sum_{j \in V}W_{i,j}V_i-\sum_{j \in V}W_{i,j}V_j=d_iV_i-W_iV\),这里调换一下\(i,j\)的位置不影响后面的推导。
用矩阵的形式就是\(\Delta V=(\Delta V_1,\Delta V_2,...)^T=(d_{1,1}V_1-W_1V,...)^T=(d_{1,1}V_1,...)^T-(W_1V,...)^T=DV-WV=(D-W)V\),其中的这个\(L=(D-W)\)就是拉普拉斯矩阵。
对于无向图,\(W,D,L\)都是对称矩阵,根据定义可得\(L\)的每一行元素之和为\(0\)(D_i的定义)。
3.归一化
(1)对称归一化
\(L'=D^{-1/2}LD^{-1/2}=I-D^{-1/2}WD^{-1/2}=I-A\),\(D^{1/2}\)是对\(D\)的每一个元素开平方根得到的
其中\(A_{i,j}=L_{i,j}/\sqrt{D_{i,i}D_{j,j}}\),\(A_{i,i}=1\)
借用一张图,图中的\(L_{sym}\)即为\(A\)
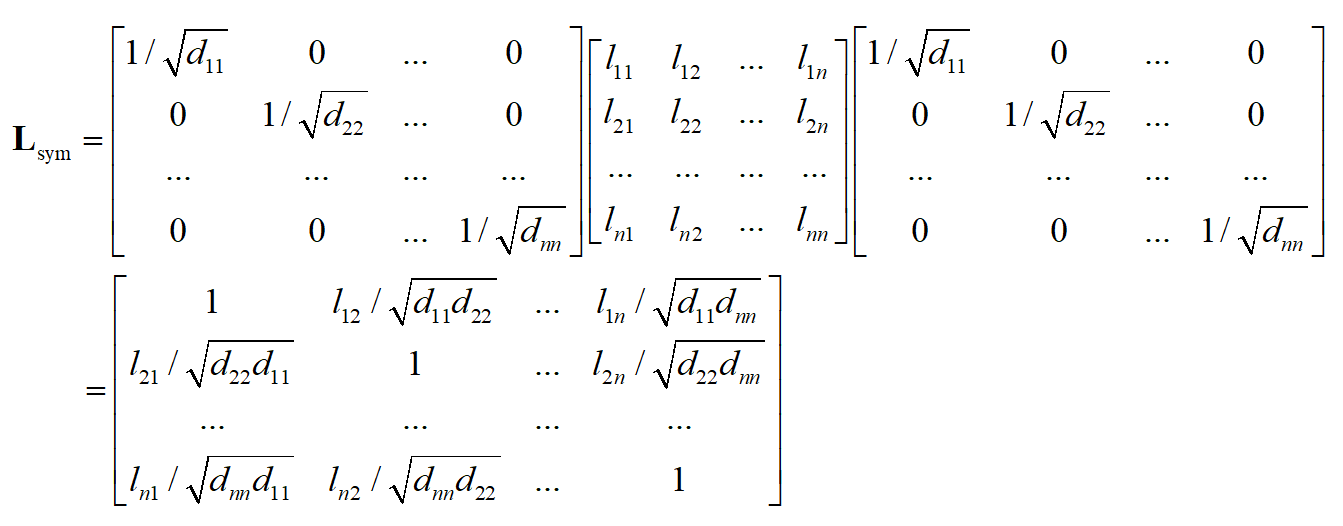
(2)随机漫步归一化
\(L'=D^{-1}L=I-D^{-1}W=I-A\)
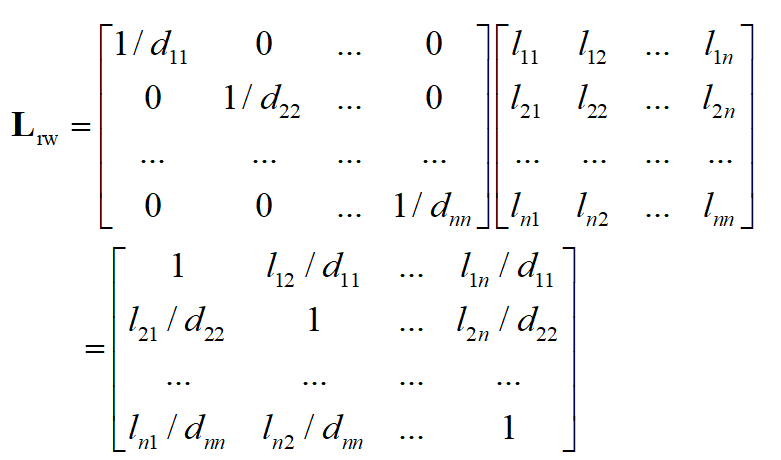


 浙公网安备 33010602011771号
浙公网安备 33010602011771号