【笔记】组合数学初步

\(\S1.\) 二项式系数

1.1 定义

我们在高中时常见的二项式系数的形式是

\[C_{n}^{k} = \frac{n!}{k!(n-k)!} \]

但下文将采用如下的定义：

\[\binom{n}{k} = \begin{cases}\dfrac{n^{\underline{k}}}{k!} & k \ge 0\\\\0 & k < 0\end{cases} \]

注意这里对 \(n\) 没有做任何限制，意味着 \(n < 0\) 时，\(\dbinom{n}{k}\) 也是有定义的。

1.2 基础性质/恒等式

让我们从熟悉的性质开始：

1. （对称恒等式） \(\dbinom{n}{k} = \dbinom{n}{n-k}\)

2. （加法公式）\(\dbinom{n}{k} = \dbinom{n-1}{k}+\dbinom{n-1}{k-1}\)

3. （吸纳/提取恒等式）\(\dbinom{n}{k} = \dfrac{n}{k}\dbinom{n-1}{k-1}\)

4. （二项式公式）\((x-y)^n = \sum\limits_{k = 0}^{n}\dbinom{n}{k}x^ky^{n-k}\)

之后是关于 \(n < 0\) 的情况：

\[\begin{aligned} \binom{-n}{k} &= \frac{(-n)^{\underline{k}}}{k!}\\ &= \frac{(-n)(-n-1)\cdots(-n-k+1)}{k!}\\ &= \frac{(-1)^k(n+k-1)(n+k-2)\cdots(n+1)n}{k!}\\ &= (-1)^k\binom{n+k-1}{k} \end{aligned} \]

那么就可以总结出

5. （上指标反转）\(\dbinom{n}{k} = (-1)^k\dbinom{k-n-1}{k}\)

接下来是一些关于求和的性质：

6. （平行求和）\(\sum\limits_{k \le n}\dbinom{r+k}{k} = \dbinom{r+n+1}{n}\)

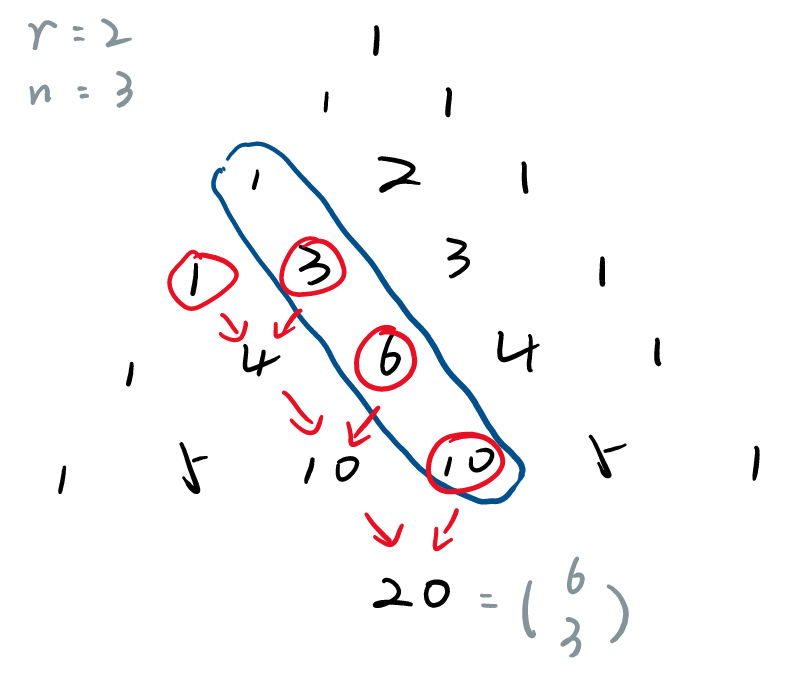
有限微积分

其实我们也有另一个写法

\[\sum\binom{r+x}{x}\delta x = \binom{r+x}{x-1}+C \]

所以

\[{\sum}_{0}^{n+1}\binom{r+k}{k} \delta x = \binom{r+n+1}{n}-\binom{r}{-1} = \binom{r+n+1}{n} \]

7. （上指标求和）\(\sum\limits_{0 \le k \le n}\dbinom{k}{m} = \dbinom{n+1}{m+1}\)

有限微积分

同上

\[\sum\binom{x}{m}\delta x = \binom{x}{m+1}+C \]

所以

\[{\sum}_{0}^{n+1}\binom{x}{m} \delta x = \binom{n+1}{m}-\binom{0}{m} = \binom{n+1}{m} \]

1.3 二项式系数乘积的和

1. \(\sum\limits_{k}\)

\(\S2.\) 生成函数

\(\S3.\) 卡特兰数

\(\S4.\) 一些问题

4.1 错排

一个邮差给 \(n\) 个人各送一封信，问没有人收到自己的信的情况数？