二分查找

二分查找主要是通过查找有序数组，依据中值判定target所在的区域，达到时间复杂度缩减为O（nlogn）的目的。

主要值是left（左边界），right（右边界），mid（中值），mid 根据 left 和 right 的变化而变化。

典型例题

1、基本算法

int search(vector<int> nums,int target){
        int left = 0;
        int right = nums.size()-1;
        while(left<=right){
            int mid = (left+right)/2;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]<target){
                left = mid + 1;
            }else if(nums[mid]>target){
                right = mid - 1;
            }
        }
        return false;
    }            

2、搜索轮转二叉树

题目简介：

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

题目分析：

先通过nums[0]和nums[mid]的比较确定那一块是有序的，再通过nums【0】、nums【mid】和target的对比确定target是在有序的块内还是在无序的块内，在有序的块内进行二分查找找到，在无序的块内嵌套之前的运算，在无序块的有序块内接着二分查找。

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环. 

解析代码：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = (int)nums.size();
        if (!n) {
            return -1;
        }
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        // l左边界，r右边界
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            // 查找到需要的元素
            if (nums[mid] == target) return mid;
            // 左边有序
            if (nums[0] <= nums[mid]) {
                // target在左边有序的里
                if (nums[0] <= target && target < nums[mid]) {
                    r = mid - 1;
                } 
                // target不在左边有序的里
                else {
                    l = mid + 1;
                }
            } 
            // 右边有序
            else {
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
};

 2、搜索二维矩阵

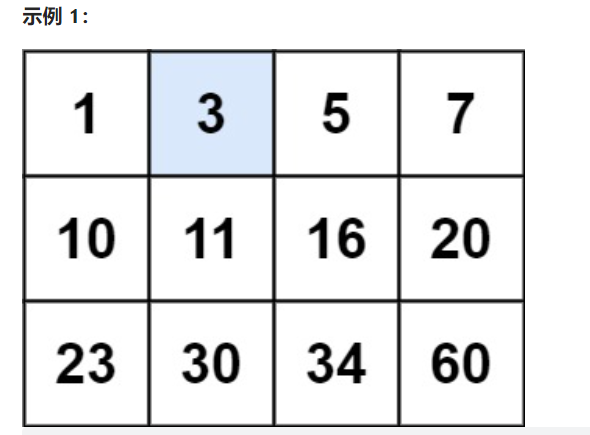
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

 

解决代码：

class Solution {
public:
//二分查找标准算法
    bool search(vector<int> nums,int target){
        int left = 0;
        int right = nums.size()-1;
        if(target<nums[left]||target>nums[right]){
            return false;
        }
        while(left<=right){
            int mid = (left+right)/2;
            if(nums[mid]==target){
                return true;
            }else if(nums[mid]<target){
                left = mid + 1;
            }else if(nums[mid]>target){
                right = mid - 1;
            }
        }
        return false;
    }

    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        bool flag = false;
        int pos = 0;
        int sizeMax = matrix.size();
        if(target<matrix[0][0]){
            return flag;
        }
        for(pos;pos<sizeMax;pos++){
            //确定在哪个区间内，在二分查找确定是否存在值
            if(target<=matrix[pos][matrix[pos].size()-1]&&target>=matrix[pos][0]){
                flag = search(matrix[pos],target);
                break;
            }
        }
        return flag;
    }
};