推荐模型之矩阵分解【学习笔记】

来源：老弓的学习笔记

协同过滤的进化-矩阵分解算法MF

针对问题：

1.协同过滤处理【稀疏矩阵】的能力弱 2.维护相似度矩阵难度大

解决思路：

引例：

 

 那些音乐风格相当于是个隐向量

用隐向量，给每个用户与每首音乐打上标签。

 

实际应用中

 

 k是自己指定的。k越大 表达信息越强

 

视频3 特征值分解

MF的几种方式：

 

 特征值分解：

特征值、特征向量:

 

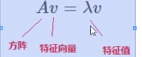
 特征值分解：

 

 只适用于方阵

 

奇异值分解SVD

定义：

 

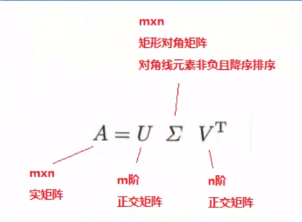
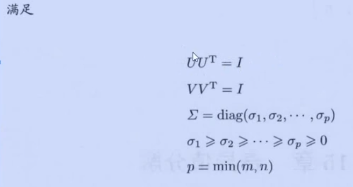
 示例：

 

 矩阵A的奇异值分解中，奇异值是唯一的，而矩阵U和V不是唯一的。

 

视频05 奇异值分解计算步骤

奇异值分解的基本定理：

 

 任意给定一个实矩阵，其奇异值分解一定存在。

 

奇异值分解计算步骤：

 

 实对称矩阵：矩阵与其转职 相等就是 实对称矩阵

 

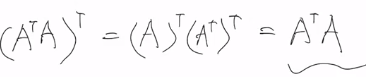
 所以它是实对称矩阵

 

 

 

 

 

 

 

 （自注疑问：这里不知道为啥这样就变成正交矩阵了 正交矩阵×它转置等于单位矩阵）

 

 

 

 

 

 

 

 

 

 

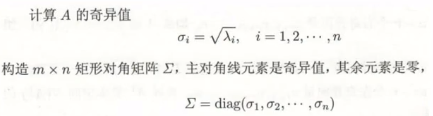
 求标准正交基可以看统计学习方法的例子

 

 

视频6 奇异值分解 缺点

 

 

 

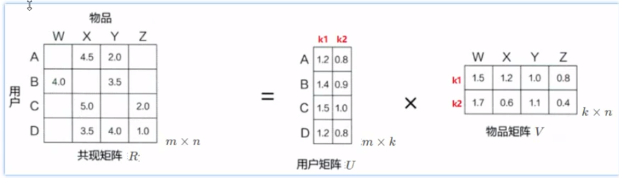
 结论：不适合用于解决大规模稀疏矩阵的矩阵分解问题。

 

视频7 Basic SVD   LFM   Funk SVD  这三个都是同一个东西

将矩阵分解问题转化为最优化问题，通过梯度下降进行最优化。

预测函数：

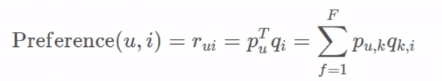rui为某个用户对某个物品的评分值

 损失函数：

 

 为了方便梯度下降 加一个二分之一

优化目标

 

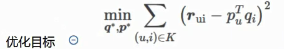
 梯度下降：

求梯度：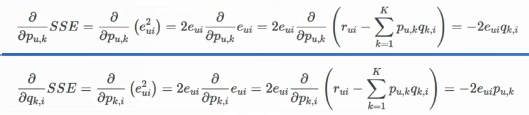

 

 

 

 

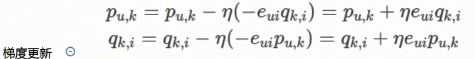
具体的步骤：

 

 

 

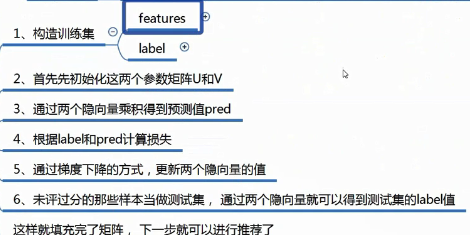
视频8 RSVD

在Basic SVD的基础上加入正则化函数 以防止过拟合。

 

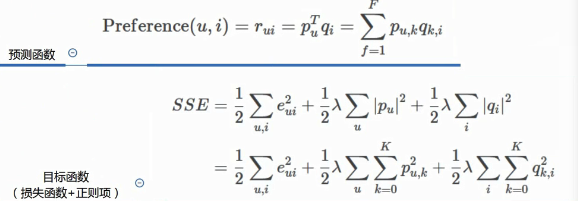
RSVD进一步优化：消除用户和物品打分的偏差

 

 

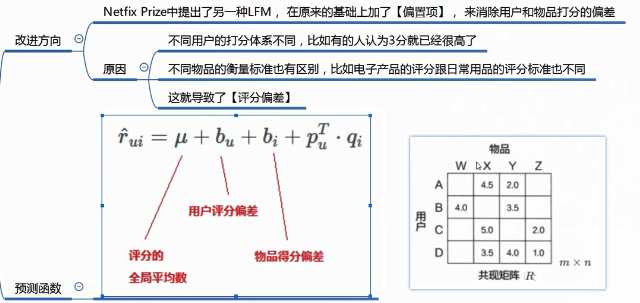
9 SVD++

10 MF的优点及局限性