dls的数论-阶与原根，指数方程

阶

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
vector<int> pf;

LL qmi(LL a, LL b, LL mod){
    LL res = 1 % mod;
    while(b){
        if(b&1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int main(){
    int p, T; scanf("%d %d", &p, &T);
    int m = p - 1;
    for(int i = 2; i <= m / i; i ++){
        if(m % i == 0){
            pf.push_back(i);
            while(m % i == 0) m /= i;
        }
    }
    if(m != 1) pf.push_back(m);
    while(T--){
        int x; scanf("%d", &x);
        int res = p - 1;
        for(auto pp : pf){
            while(res % pp == 0 && qmi(x, res / pp, p) == 1) res /= pp;
        }
        printf("%d\n", res);
    }    
    return 0;
}

原根

循环节的长度是f(m),1-m之间与m互质的数是f(m)个，这些数是一样
g是一个原根，g^i 1-f(m)能表示上面所有的数

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
int pf[100010];

LL qmi(LL a, LL b, LL mod){
    LL res = 1 % mod;
    while(b){
        if(b&1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int main(){
    int T; scanf("%d", &T);
    while(T--){
        int p; scanf("%d", &p);
        int m = p - 1;
        int t = 0;
        for(int i = 2; i <= m / i; i ++){
            if(m % i == 0){
                pf[t ++] = i;
                while(m % i == 0) m /= i;
            }
        }
        if(m != 1) pf[t ++] = m;
        for(int g = 1; ; g ++){
            int suc = true;
            for(int i = 0; i < t; i ++ ){
                int pp = pf[i];
                if(qmi(g, (p - 1) / pp, p) == 1){
                    suc = false;
                    break;
                }
            }
            if(suc){
                printf("%d\n", g);
                break;
            } 
        }       
    }
 
    return 0;
}

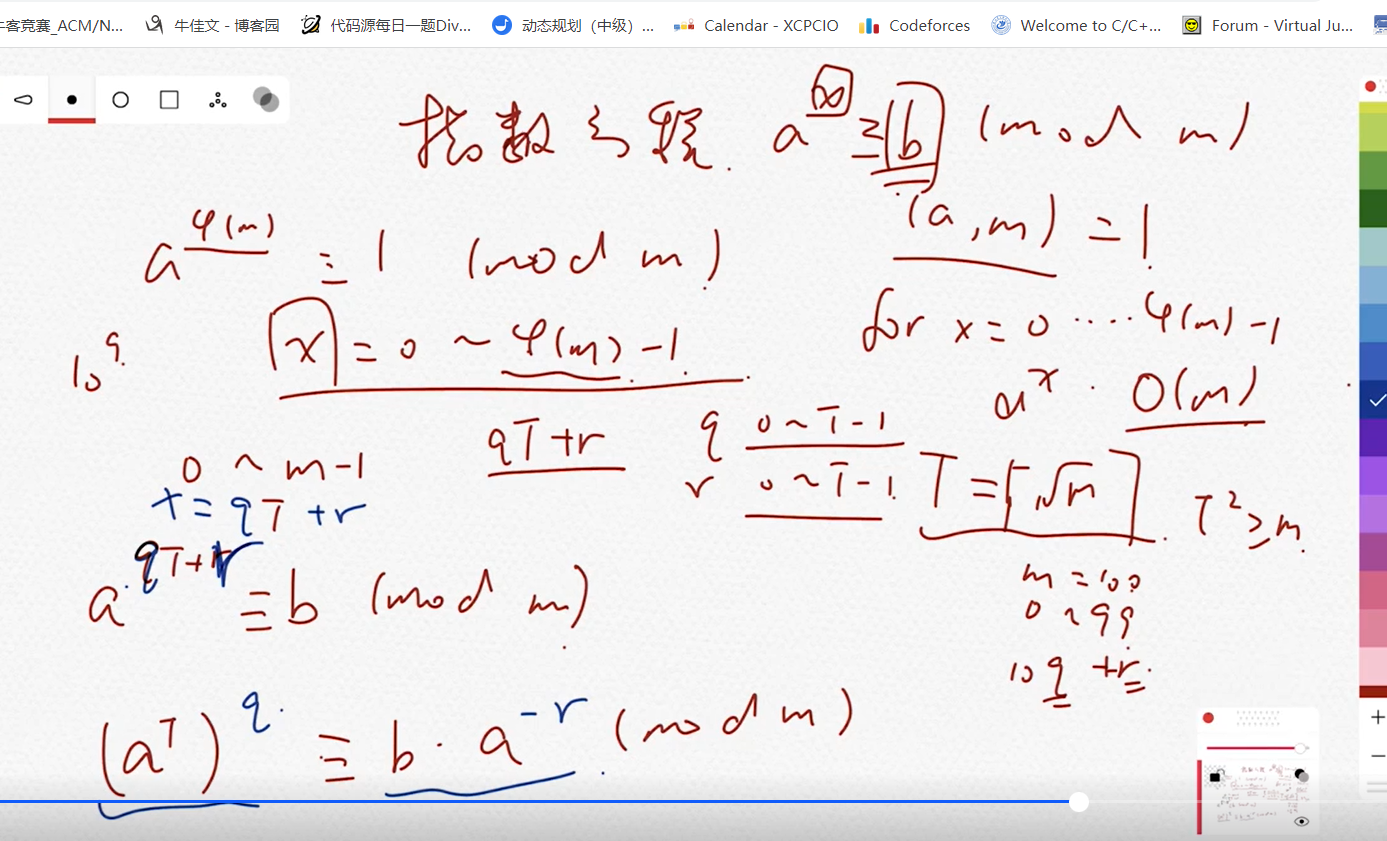
int bsgs(int a, int b, int p){
    if(1 % p == b % p) return 0;
    
    unordered_map<int, int> h;
    int k = sqrt(p) + 2;
    int B = b % p;
    for(int i = 0; i < k; i ++){
        h[B] = i;
        B = (LL)B* a % p;
    }
    int Ak = 1, A = 1;
    for(int i=1; i<=k; i++) Ak = (LL)Ak * a % p;
    A = Ak;
    for(int i=1; i<=k; i++){
        if(h.count(A)) return i * k - h[A];
        A = (LL) A * Ak % p;
    }
    return -1;
}