查找算法
查找算法
查找算法分类
- 顺序(线性)查找
- 二分查找/折半查找
- 插值查找
- 斐波那契查找
线性查找
有一个数列: {1,8, 10, 89, 1000, 1234} ,判断数列中是否包含此名称【顺序查找】 要求: 如果找到了,就提示找到,并给出下标值
代码实现
public static ArrayList<Integer> LineFound(int[] arr, int value) {
ArrayList<Integer> list = new ArrayList<Integer>();
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value) {
list.add(i);
}
}
return list;
}
二分查找
请对一个有序数组进行二分查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"
思路分析
- 首先确定该数组中间值下标
- 接着需要查找的值与中间值比较
- 大于中间值,向右递归
- 小于中间值,向左递归
- 等于中间值,返回中间值
- 什么时候我们要结束递归
- 找到我们结束递归
- 当我们递归完整个数组没有找到时,我们也需要结束递归。
代码实现
------------------------方法一 利用递归实现-------------------
public static int BinnarySearch(int[] arr, int value, int left, int right) {
if (left > right) {
return -1;
}
int mid = left + right / 2;
if (value < arr[mid]) {
right = mid - 1;
return BinnarySearch(arr, value, left, right);
} else if (value > arr[mid]) {
left = mid + 1;
return BinnarySearch(arr, value, left, right);
} else {
return mid;
}
}
}
---------------------方法二 利用While实现-------------------
public static int BinarySearch2(int[] arr, int value){
int left=0;
int right=arr.length-1;
while(right >= left){
int mid=(right-left)>>1;
if(value>arr[mid]){
left=mid+1;
}else if(value<arr[mid]){
right=mid-1;
}
else{
return mid;
}
}
return -1;
}
二分算法改进
思路分析
- 当我们找到mid时,我们不要直接返回
- 向mid的左边扫描,添加到集合中
- 接着添加mid
- 接着向右边扫描,添加到集合中
代码实现
public static ArrayList<Integer> BinarySearch(int[] arr, int value, int left, int right) {
ArrayList<Integer> list = new ArrayList<Integer>();
if (left > right) {
return null;
}
int mid = left + right / 2;
if (value < arr[mid]) {
right = mid - 1;
return BinarySearch(arr, value, left, right);
} else if (value > arr[mid]) {
left = mid + 1;
return BinarySearch(arr, value, left, right);
} else {
int temp = mid-1;
while (true){
if(temp<0 || arr[temp]!=value){
break;
}
list.add(temp);
temp--;
}
list.add(mid);
temp = mid+1;
while (true){
if(temp>arr.length-1 || arr[temp]!=value){
break;
}
list.add(temp);
temp++;
}
return list;
}
}
插值算法
请对一个有序数组进行插值查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"。
算法思想
- 插值查找算法类似于二分查找,不同的是插值查找每次从自适应 mid 处开始查找。
- int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])
- 其他算法思想跟二分查找算法一样
代码实现
public static int InsertSearch(int[] arr, int value, int left, int right) {
//必须要对查找的值判断,因为查找的值参与运算,如果查找的值非常大的时候,可能会出现越界
if (left > right || value < arr[0] || value > arr[arr.length - 1]) {
return -1;
}
int mid = left + (right - left) * (value - arr[left]) / (arr[right] - arr[left]);
if (value < arr[mid]) {
right = mid - 1;
return InsertSearch(arr, value, left, right);
} else if (value > arr[mid]) {
left = mid + 1;
return InsertSearch(arr, value, left, right);
} else {
return mid;
}
}
总结
- 对于数据量大,关键字分布比较均匀的查找表来说,采用插值查找, 速度较快
- 关键字分布不均匀的情况下,该方法不一定比折半查找要好
斐波那契查找算法
请对一个有序数组进行斐波那契查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"。
思路分析
- 斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid 不再是中间或插值得到,而是位于黄金分割点附近,即 mid=low+F(k-1)-1(F 代表斐波那契数列),如下图所示
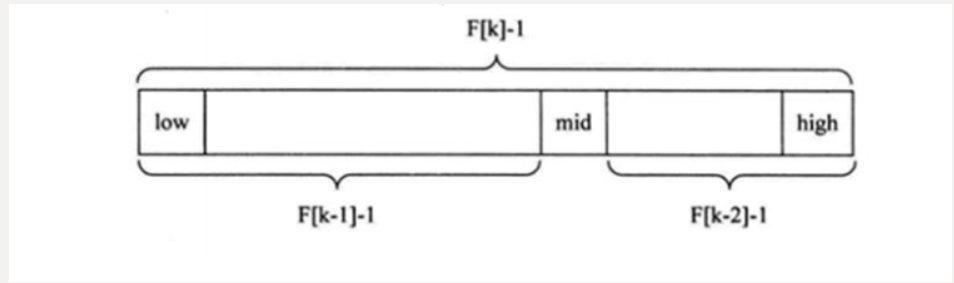
对 F(k-1)-1 的理解:
-
由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质,可以得到 (F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1 。该式说明:只要顺序表的长度为 F[k]-1,则可以将该表分成长度为 F[k-1]-1 和 F[k-2]-1 的两段,即如上图所示。从而中间位置为 mid=low+F(k-1)-1;
-
但顺序表长度 n 不一定刚好等于 F[k]-1,所以需要将原来的顺序表长度 n 增加至 F[k]-1。这里的 k 值只要能使得 F[k]-1 恰好大于或等于 n 即可,顺序表长度增加后,新增的位置(从 n+1 到 F[k]-1 位置),都赋为 n 位置的值即可
代码分析
//斐波那契查找
public static int fbnaccSearch(int[] arr, int value) {
int left = 0;
int right = arr.length - 1;
int mid=0;
int k=0;//表示斐波那契分割数值的下标
int[] f = fb(20);//获取到斐波那契数列
//顺序表长度right不一定刚好等于 f[k]-1,所以需要将原来的顺序表长度增加至 f[k]-1。
while(right > f[k]-1){
k++;
}
//顺序表长度增加后,新增的位置(从 right+1 到 f[k]-1 位置),都赋为 right位置的值
int[] temp = Arrays.copyOf(arr, f[k] - 1);
for(int j = right+1;j < temp.length;j++){
temp[j] = arr[right];
}
while (right >= left) {
mid = left + f[k-1]-1;
if (value > temp[mid]) {
left = mid + 1;
k-=2;
} else if (value < temp[mid]) {
right = mid - 1;
k-=1;
} else {
if(mid<right){
return mid;
}
else{
return right;
}
}
}
return -1;
}
//生成斐波那契数组
public static int [] fb(int maxsize){
int [] fb=new int [maxsize];
fb[0]=1;
fb[1]=1;
for(int i=2;i<maxsize;i++){
fb[i]=fb[i-1]+fb[i-2];
}
return fb;
}
总结
当查找数组长度小于5时,可能会出现数组越界异常。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号