λ表达式与邱奇数，JAVA与JS的lamda表达式实现

前言

　　学习 λ 演算的初衷是为了更好的使用 JAVA8 的 lamda表达式，但是在学习过程中发现 λ 演算的作用和深度远远比想象的大的多得多。λ 演算的定义并不复杂，包括一条变换规则（变量替换）和一条函数定义方式，但其外延却囊括和渗透到了无数方向，乃至学习过程中脑中不断冒出一句话：内涵越小、外延越大。 λ 表达式简直是简洁美的典范。

　　目前对 λ 表达式的认知还处于初级阶段，对其核心认知停留在以下几点（以程序员的视角看），后面会随着学习的深入继续补充：

　　1. λ 表达式的重要性在于其二面性：既可以描述一个计算过程，也可以被看做一个数学对象用于证明一些命题。

　　2. 其与可计算性具有等价关系（等价于图灵机），能有效计算的函数等价于 λ 可定义性，也就是说我们可以用 λ 表达式合法的定义的函数都是可计算的（可用程序正确描述）。

　　3. 基于2，可计算程序一定是 λ 可定义的，我们可以将复杂的程序简化为 λ 演算，以此理解程序的行为。基于1，λ 演算以函数为单位，将程序简化为 λ 演算后可以更好的借助数学公理推演和证明程序的正确性。

　　4. 在实际编程过程中，λ 表达式也被广泛的运用着。比如匿名函数的使用（有时我们也成为了 lamda 表达式）、利用规约策略建模求值策略（归约策略的不同和函数式编程中的及早求值还有惰性求值之间的不同有关，比如像 JAVA、C++ 等强类型语言通常采用应用次序和传值调用归约，但通常被成为及早求值策略）、对并行/并发编程的理论支持（在λ-演算的基础上，发展起来的π-演算、χ-演算，成为近年来的并发程序的理论工具之一，许多经典的并发程序模型就是以π-演算为框架的。）

　　更令人眼前一亮的是邱奇计数及其运算，这让我从另一个角度来理解计算与函数。我尝试借助 JAVA 的 lamda 表达式来实现邱奇计数及其计算，但由于语法特性（受限于个人水平）其实现并不是完全贴近原生的 λ 演算，希望能得到广大网友的纠错或指点。

背景

　　现代形式科学的所有的故事都来自于莱布尼茨的两大梦想：第一、建立一套严格精密的人工语言，这种语言没有人类语言的歧义多结构，可以精确地描述任何哲学、逻辑和数学问题；第二、找到一种方法，利用这套“普遍语言”，解决任何科学、哲学和数学的问题。　　

　　莱布尼茨的梦想，在20世纪先后成真：集合论和符号逻辑、计算科学。而这一切的一切都源自19世纪末20世纪初发生的第三次数学危机。这场危机的结果使得数学、逻辑学和哲学发生了脱胎换骨的变化，数学的公理化、逻辑学的数学化、哲学的逻辑化是这个伟大变革中最显著的特点。

　　在此背景下，弗雷格的一阶谓词逻辑，则第一次明确地确立了逻辑是数学的基础的立场，亦即，对数学命题的严格描述，只能借助精密严格的人工语言——一阶谓词逻辑才可以完成，这也是当年弗雷格的先辈——莱布尼兹的宏大构想之一。弗雷格企图借助最基础的逻辑概念，建立一个一阶逻辑的形式系统，包括一套人工语言和一套推理规则来定义数学的基本概念。

　　邱奇是个美国逻辑学家，生于 1903 年。他在 1928 年开始构造的一个形式系统中包含了纯λ演算。他发明这一形式系统的初衷是为了给逻辑学提供一个基础，能代替罗素的类型理论和恩斯特·策梅洛（Ernst Zermelo）的集合理论。这个系统 1932 年发表后不久就被发现有矛盾，于是一年后邱奇修正了一番重新发表。当时的人对不完备性定理威力有多大还缺乏清醒广泛的认识。所以他还希望那时发现不久的哥德尔关于 “数学原理” 一书的不完备性定理不会扩展到他的系统上。

　　但愿望是良好的，结果是残酷的。到 1935 年，邱奇的两个学生， Stephen Kleene 和 Barkley Rosser 发现邱奇的逻辑系统是不一致的。不过柳暗花明又一村，他们发现系统包含的纯 演算则具有一系列良好的性质，再后来更是证明用 演算可以等价的定义出可计算函数，邱奇觉得能有效计算的函数等价于λ可定义性，这就是著名的 “邱奇 –图灵论题” 的一部分了。更一进步的，邱奇用λ演算证明了一阶逻辑不存在递归判定过程，这是对希尔伯特提出的判定性问题（Entscheidungsproblem）的第一个否定性答案，这比用图灵证明停机问题不可判定还要早几个月。

　　不过二十世纪三十年代在 演算方面的成果差不多也就这些了，再接下来的 20 年都没有太多研究和进展。直到六十年代，那时有了计算机，有了程序设计语言，有了计算机科学家。在 1965 年，英国计算机科学家 Peter Landin 发现可以通过把复杂的程序语言转化成简单的λ演算，来理解程序语言的行为。这个洞见可以让我们把 λ 演算本身看成一种程序设计语言。而众所周知的 John McCarthy 的Lisp 语言，更是让λ演算广为传播。现在不论是各种实际的程序设计语言还是理论上的研究工作，λ演算都是一个绕不过去的基本工具了。

概述

　　λ演算的作用是用逻辑方法解决数学基础问题、是由美国数学家、逻辑学家Alonzo Church提出的类似组合子逻辑的方案。

　　λ演算的基本思想和组合子逻辑相同，只是实现的技术细节不同。例如，λ演算中，函数也是最基本元素，也包含“应用”的概念，而且和组合子逻辑基本相同，但是对如何从已知函数定义或者派生出新的函数，方法上却完全不同。上面讲到，在组合子逻辑中，已经没有变量的概念，所有新函数的生成，都是靠S和K这两个基本“运算符”（高阶函数）的组合完成，而λ演算，则将函数的定义看做是原生的操作之一，看做是“公理”，具体的技术实现就是“函数抽象”；函数抽象就是，函数的建立过程是独立的，不会再从更基本的公理、定理出发，而只根据函数本身的变量和值定义，换句话说，是根据函数的外延性定义。

　　定义公式就是：λx.y，表示ƒ(x) = y。如果你是第一次看见这个符号，千万不要把前面那个希腊字母看做是和ƒ一样的“函数符号”，它不是！那λ表示什么呢？如果硬要牵强地比喻，这个λ更像是谓词逻辑中的量词符号∀或∃。因为逻辑符号从来就不是统一的，即使到了今天仍然如此。弗雷格曾经使用ἑ表示量词，在罗素、怀特海时代x̂常被用来表示约束变量，当时由于排版的原因，往往被写成了∧x，而在视觉上，逻辑符号∧和大写希腊字母Λ经常混淆，所以Church最终决定用希腊小写字母λ表示函数的变量抽象。因此λx.y的正确解读应当是表达式y中变量x的抽取——抽象化，表示变量x与表达式y内某一变量的互动关系。　　

　　演算之所以这么重要，用 Benjamin C. Pierce 的话说在于它具有某种 “二象性”：它既可以被看作一种简单的程序设计语言，用于描述计算过程，也可以被看作一个数学对象，用于推导证明一些命题。

内容

　　λ演算可以被称为最小的通用程序设计语言。它包括一条变换规则（变量替换）和一条函数定义方式。

　　λ演算表达了两个计算机计算中最基本的概念“代入”和“置换”。“代入”我们一般理解为函数调用，或者是用实参代替函数中的形参；“置换”我们一般理解为变量换名规则。“代入”就是用lambda演算中的β-归约概念。而“替换”就是lambda演算中的α-变换。

　　在 lambda 演算中有许多方式都可以定义自然数，但最常见的还是邱奇数 。

　　邱奇编码是把数据和运算符嵌入到lambda演算内的一种方式，它是使用lambda符号的自然数的表示法。这种方法得名于阿隆佐·邱奇，他首先以这种方法把数据编码到lambda演算中。

　　Church数是在Church编码下的自然数的表示法。表示自然数n的高阶函数是把任何其他函数 f 映射到它的n重函数复合的函数。

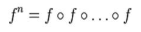
　　在λ演算中，计算系统用函数的嵌套次数来计数。

　　lambda演算中的数字n就是一个把函数 f 作为参数并以 f 的n次幂为返回值的函数。

 　　关于 λ 演算的用法有非常多，下面我们仅介绍最基本的三个方面：α-变换、β-归约、邱奇计数及其 JAVA 实现。

α-变换

　　Alpha-变换规则表达的是，被绑定变量的名称是不重要的。比如说 λx.x 和 λy.y 是同一个函数。尽管如此，这条规则并非像它看起来这么简单，关于被绑定的变量能否由另一个替换有一系列的限制。

　　Alpha-变换规则陈述的是，若 V 与 W 均为变元，E 是一个 lambda 表达式，同时 E[V/W] 是指把表达式 E 中的所有的 V 的自由出现都替换为 W，那么在 W 不是 E 中的一个自由出现，且如果 W 替换了 V，W 不会被 E 中的 λ 绑定的情况下，有

　　λ V. E == λ W. E[V/W]

　　这条规则告诉我们，例如 λ x. (λ x. x) x 这样的表达式和 λ y. (λ x. x) y 是一样的。

β-归约

　　Beta-消解规则表达的是函数作用的概念。它陈述了若所有的 E' 的自由出现在 E [V/E' ] 中仍然是自由的情况下，有 ((λ V. E ) E' ) == E [V/E' ]  成立。（这句听起来不好理解，通俗的说便是，以 E'  为实参带入 表达式 E 中的形参后，E'  中的自由变量没有被 λ V 绑定）

　　== 关系被定义为满足上述两条规则的最小等价关系 (即在这个等价关系中减去任何一个映射，它将不再是一个等价关系)。

　　对上述等价关系的一个更具操作性的定义可以这样获得：只允许从左至右来应用规则。不允许任何 beta 消解的 lambda 表达式被称为范式。并非所有的 lambda 表达式都存在与之等价的范式，若存在，则对于相同的形式参数命名而言是唯一的。此外，有一个算法用户计算范式，不断地把最左边的形式参数替换为实际参数，直到无法再作任何可能的消解为止。这个算法当且仅当 lambda 表达式存在一个范式时才会停止。Church-Rosser 定理 说明了，当且仅当两个表达式等价时，它们会在形式参数换名后得到同一个范式。

　　我们来看以下β-归约的具体的例子：

 

 

　　从上面的例子可以看出， 缩减虽然名为缩减，但实际情况是复杂的。像最后这两个例子，一个永远缩减为自身，一个甚至更糟糕，越来越长，非但不是缩减反而是增长了。并不是所有的 λ 项都能 β-规约到 β-范式。这其实还不是最让人担心的，更糟糕的是 β-规约的定义非常 “狡猾”，或者叫非常含糊，它只要求存在一个有限长的 缩减链就行，当 λ 项中含有不止一个 可约式的时候，可以有不同顺序的缩减方式。

 

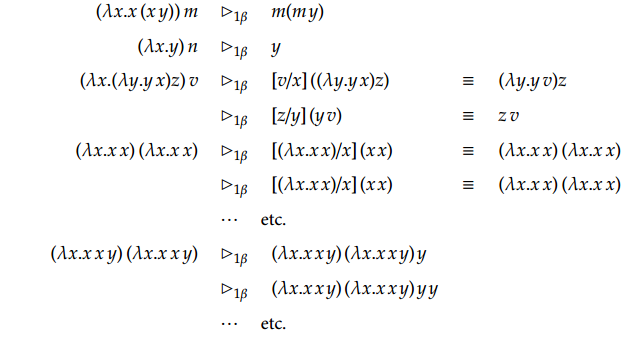
　　那让我们再来看一个例子 (𝜆x.(𝜆y.yx)𝑧)𝑣 最外层的 (𝜆 … )v 是一个 β-可约式，里层的(𝜆y.y𝑥)z 也是一个 β-可约式。那么就有两种缩减顺序：

 

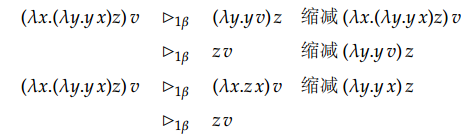
　　可以看到，虽然缩减顺序不一样，但最后得到了同样的结果。这个是不是对所有的 项

都成立呢？要是不成立，也就说顺序会影响规约结果，就不好了。这个问题的答案可以说既让人满意也让人不满意。

　　我们在进行规约时，应总是先 β-缩减最左侧最外侧的 β-可约式，若这个过程能无限进行下去，那么对 λ 项的所有任意顺序的规约都能无穷进行下去。换而言之，要是有 β-范式，那么这种最左最外侧优先的规约方式总能保证得到那个 β-范式，这种规约顺序又称为正则序。我的解释器实现的规约顺序就是正则序，虽然它规约需要的步数可能较多，但抵消不了这个巨大的优势。到目前为止，我们得到的结果都是满意的：一个 项若是有 β-范式，那么这个 β-范式某种程度上是唯一的，而且我们有确定的规约顺序保证得到这个范式。下面就只有一个问题了：能否有一个通用算法，判定一个 项是否有 范式？非常不幸，答案是否定的。

邱奇计数

　　在 lambda 演算中有许多方式都可以定义自然数，但最常见的还是Church 整数，下面是它们的定义：

　　0 = λ f. λ x. x

　　1 = λ f. λ x. f x

　　2 = λ f. λ x. f (f x)

　　3 = λ f. λ x. f (f (f x))

　　以此类推。直观地说，lambda 演算中的数字 n 就是一个把函数 f 作为参数并以 f 的 n 次幂为返回值的函数。换句话说，Church 整数是一个高阶函数 -- 以单一参数函数 f 为参数，返回另一个单一参数的函数。

　　(注意在 Church 原来的 lambda 演算中，lambda 表达式的形式参数在函数体中至少出现一次，这使得我们无法像上面那样定义 0) 在 Church 整数定义的基础上，我们可以定义一个后继函数，它以 n 为参数，返回 n + 1：

　　SUCC = λ n. λ f. λ x. f (n f x)

　　加法是这样定义的：

　　PLUS = λ m. λ n. λ f. λ x. m f (n f x)

　　PLUS 可以被看作以两个自然数为参数的函数，它返回的也是一个自然数。你可以试试验证

　　PLUS 2 3 与 5

　　是否等价。乘法可以这样定义：

　　MULT = λ m. λ n. m (PLUS n) 0,

　　即 m 乘以 n 等于在零的基础上 n 次加 m。另一种方式是

　　MULT = λ m. λ n. λ f. m (n f)

　　正整数 n 的前驱元 (predecessesor) PRED n = n - 1 要复杂一些：

　　PRED = λ n. λ f. λ x. n (λ g. λ h. h (g f)) (λ u. x) (λ u. u)

　　或者

　　PRED = λ n. n (λ g. λ k. (g 1) (λ u. PLUS (g k) 1) k) (λ l. 0) 0

　　注意 (g 1) (λ u. PLUS (g k) 1) k 表示的是，当 g(1) 是零时，表达式的值是 k，否则是 g(k) + 1。

　　JAVA实现如下：

package functions;

import org.apache.catalina.LifecycleState;

import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.function.Consumer;
import java.util.function.Function;

/**
 * @Author Nxy
 * @Date 2020/1/31 15:04
 * @Description 邱奇数定义及运算
 */
public class FuntionTest<T> {

    public static void main(String[] args) {
        String rn = System.lineSeparator();
        //定义 f 过程
        Function<Integer, Integer> f = (x) -> {
            System.out.print(x + 1);
            return x + 1;
        };
        FuntionTest<Integer> thisFun = new FuntionTest<Integer>();
        System.out.println(rn + "邱奇数 0  :");
        thisFun.zero(f, 0);
        System.out.println(rn + "邱奇数 1  :");
        thisFun.one(f, 0);
        System.out.println(rn + "邱奇数 2  :");
        thisFun.two(f, 0);
        System.out.println(rn + "邱奇数 n 表示的 4 :");
        thisFun.nf(f, 0, 4);
        System.out.println(rn + "邱奇数加 1 方法 表示的 5 :");
        thisFun.succ(f, 0, 4);
        System.out.println(rn + "邱奇数加法 表示的 5 :");
        thisFun.plus(f, 0, 2, 3);
        System.out.println(rn + "邱奇数乘 表示的 10 :");
        thisFun.mult(f, 0, 2, 5);
    }


    /**
     * 邱奇数 0，代表传入一个过程和一个入参，过程作用于入参0次 λf.λx.x
     *
     * @param f 传入的过程，用于β 规约
     * @param x 传入的参数，用于β 规约（广义的参数，也可以是过程。 λ 演算中函数是最基本的单位）
     */
    public void zero(Function<T, T> f, T x) {
        x = x;
    }

    /**
     * 邱奇数 1,代表传入一个过程和一个入参，过程作用于入参1次 λf.λx.fx
     *
     * @param f 传入的过程，用于β 规约
     * @param x 传入的过程，用于β 规约（广义的参数，也可以是过程。 λ 演算中函数是最基本的单位）
     */
    public void one(Function<T, T> f, T x) {
        f.apply(x);
    }

    /**
     * 邱奇数 2,代表传入一个过程和一个入参，过程作用于入参2次 λf.λx.ffx
     *
     * @param f 传入的过程，用于β 规约
     * @param x 传入的过程，用于β 规约（广义的参数，也可以是过程。 λ 演算中函数是最基本的单位）
     */
    public void two(Function<T, T> f, T x) {
        f.apply(f.apply(x));
    }

    /**
     * 邱奇数 n,代表传入一个过程和一个入参，过程作用于入参n次 λf.λx.nfx
     *
     * @param f 传入的过程，用于β 规约
     * @param x 传入的过程，用于β 规约（广义的参数，也可以是过程。 λ 演算中函数是最基本的单位）
     * @param n f作用于x n次
     */
    public T nf(Function<T, T> f, T x, int n) {
        //边界条件
        if (n == 0) {
            return x;
        }
        //回归条件
        if (n == 1) {
            return f.apply(x);
        }
        //嵌套作用
        return f.apply(nf(f, x, n - 1));
    }

    /**
     * 邱奇数加一 , 传入 f 作用于 x 的次数为 n+1 ， SUCC=λn.λf.λx.f(nfx)
     *
     * @param f 传入的过程，用于β 规约
     * @param x 传入的过程，用于β 规约（广义的参数，也可以是过程。 λ 演算中函数是最基本的单位）
     */
    public T succ(Function<T, T> f, T x, int n) {
        return f.apply(nf(f, x, n));
    }

    /**
     * 邱奇数加法 , 传入 f 作用于 x 的次数为 m+n 次，PLUS = λm.λn.λf.λx.mf(nfx)
     *
     * @param f 传入的过程，用于β 规约
     * @param x 传入的过程，用于β 规约（广义的参数，也可以是过程。 λ 演算中函数是最基本的单位）
     */
    public T plus(Function<T, T> f, T x, int m, int n) {
        return nf(f, nf(f, x, n), m);
    }

    /**
     * 邱奇数乘法 , 传入 f 作用于 x 的次数为 m*n 次，MULT = λm.λn.m(PLUS n)
     *
     * @param f 传入的过程，用于β 规约
     * @param x 传入的过程，用于β 规约（广义的参数，也可以是过程。 λ 演算中函数是最基本的单位）
     */
    public T mult(Function<T, T> f, T x, int m, int n) {
        return nf(f, x, m * n);
    }
    
}

运算结果：

　　以上实现仅仅是实现了邱奇数的语义，并不是完全贴近原生的定义。贴近原生的定义，则所谓的邱奇数均是函数，为入参为 f 与 x 的函数柯里化的结果，由于 JAVA 为强类型语言，其对类型的检查会导致按原生定义实现非常繁琐，我们接下来看贴近原生邱奇数的 JAVA 实现：

/**
 * @Author Nxy
 * @Date 2020/2/7 11:38
 * @Description 邱奇数定义
 */
public class FunctionTest2<T> {
    public static void main(String[] args) {
        FunctionTest2<Integer> fun2 = new FunctionTest2<Integer>();
        //测试函数 f
        Function<Integer, Integer> f = (x) -> x + 1;
        System.out.println("邱奇数0  " + fun2.zero.apply(f).apply(0));
        System.out.println("邱奇数1  " + fun2.one.apply(f).apply(0));
        System.out.println("邱奇数2  " + fun2.two.apply(f).apply(0));
        System.out.println("邱奇数3  " + fun2.three.apply(f).apply(0));
        System.out.println("邱奇数4  " + fun2.four.apply(f).apply(0));
        System.out.println("邱奇数5  " + fun2.five.apply(f).apply(0));
        System.out.println("邱奇数6  " + fun2.six.apply(f).apply(0));
    }

    /**
     * 邱奇数 0， λf.λx.x
     */
    private Function<Function<T, T>, Function<T, T>> zero = (Function<T, T> f) -> {
        Function<T, T> result = (T x) -> {
            return x;
        };
        return result;
    };


    /**
     * 邱奇数加一 ,  SUCC=λn.λf.λx.f(nfx)
     */
    private Function<Function<T, T>, Function<T, T>> succ(Function<Function<T, T>, Function<T, T>> n) {
        Function<Function<T, T>, Function<T, T>> getF = (Function<T, T> f) -> {
            Function<T, T> getX = (T x) -> {
                return f.apply(n.apply(f).apply(x));
            };
            return getX;
        };
        return getF;
    }

    /**
     * 邱奇数加法 , 传入 f 作用于 x 的次数为 m+n 次，PLUS = λm.λn.λf.λx.mf(nfx)
     */
    private Function<Function<T, T>, Function<T, T>> plus(Function<Function<T, T>, Function<T, T>> m,
                                                          Function<Function<T, T>, Function<T, T>> n) {
        Function<Function<T, T>, Function<T, T>> getF = (Function<T, T> f) -> {
            Function<T, T> getX = (T x) -> {
                return m.apply(f).apply(n.apply(f).apply(x));
            };
            return getX;
        };
        return getF;
    }

    /**
    *    邱奇数乘法 , 传入 f 作用于 x 的次数为 m*n 次，MULT = λm.λn.m(PLUS n)
    */
    private Function<Function<T, T>, Function<T, T>> mult(Function<Function<T, T>, Function<T, T>> m,
                                                          Function<Function<T, T>, Function<T, T>> n) {
        Function<Function<T, T>, Function<T, T>> getF = (Function<T, T> f) -> {
            Function<T, T> getX = (T x) -> {
                return m.apply(n.apply(f)).apply(x);
            };
            return getX;
        };
        return getF;
    };

    /**
     * 邱奇数 1,代表传入一个过程和一个入参，过程作用于入参1次 λf.λx.fx
     */
    private Function<Function<T, T>, Function<T, T>> one = (Function<T, T> f) -> {
        return succ(zero).apply(f);
    };

    /**
     * 邱奇数 2,代表传入一个过程和一个入参，过程作用于入参2次 λf.λx.ffx
     */
    private Function<Function<T, T>, Function<T, T>> two = (Function<T, T> f) -> {
        return succ(one).apply(f);
    };

    /**
     * 邱奇数 3,代表传入一个过程和一个入参，过程作用于入参3次
     */
    private Function<Function<T, T>, Function<T, T>> three = (Function<T, T> f) -> {
        return plus(one, two).apply(f);
    };

    /**
     * 邱奇数 4,代表传入一个过程和一个入参，过程作用于入参4次
     */
    private Function<Function<T, T>, Function<T, T>> four = (Function<T, T> f) -> {
        return mult(two,two).apply(f);
    };

    /**
     * 邱奇数 5,代表传入一个过程和一个入参，过程作用于入参5次
     */
    private Function<Function<T, T>, Function<T, T>> five = (Function<T, T> f) -> {
        return plus(two, three).apply(f);
    };

    /**
     * 邱奇数 6,代表传入一个过程和一个入参，过程作用于入参6次
     */
    private Function<Function<T, T>, Function<T, T>> six = (Function<T, T> f) -> {
        return mult(two, three).apply(f);
    };
}

　　执行结果：

 　　好了，让我们从 JAVA 的类型检查中解放出来，看一下弱类型语言 JS 对邱奇数的实现：

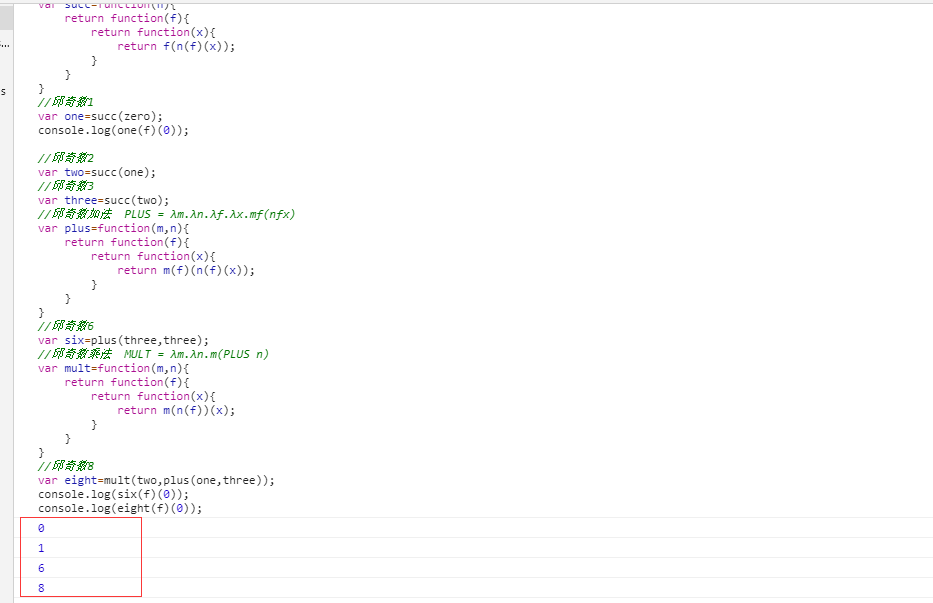
//虚拟目标函数 f
function f(x){
    return x+1;
}
//邱奇数0
var zero=function(f){
    return function(x){
        return x;
    }
}
console.log(zero(f)(0));
//邱奇数加一, SUCC=λn.λf.λx.f(nfx)
var succ=function(n){
    return function(f){
        return function(x){
            return f(n(f)(x));
        }
    }
}
//邱奇数1
var one=succ(zero);
console.log(one(f)(0));

//邱奇数2
var two=succ(one);
//邱奇数3
var three=succ(two);
//邱奇数加法  PLUS = λm.λn.λf.λx.mf(nfx)
var plus=function(m,n){
    return function(f){
        return function(x){ return m(f)(n(f)(x));
        }
    }
}
//邱奇数6
var six=plus(three,three);
//邱奇数乘法  MULT = λm.λn.m(PLUS n)
var mult=function(m,n){
    return function(f){
        return function(x){
            return m(n(f))(x);
        }
    }
}
//邱奇数8
var eight=mult(two,plus(one,three));
console.log(six(f)(0));
console.log(eight(f)(0));

　　为了验证正确性，我们只打印的 邱奇数0 、邱奇数1 、邱奇数6 和邱奇数8：