数据结构入门:顺序表/链表/栈/队列/堆(原理+实现)
一、开篇引入
作为计算机专业的学生,顺序表、链表、栈、队列、堆是《数据结构》课程的核心基础,也是算法刷题、工程开发的"必备工具",但新手刚接触时,常容易混淆各结构的特性,也难以用C语言实现,本文就从概念原理出发,用C语言完成这些数据结构的实现,手把手帮助新手彻底搞懂这些核心结构。
二、数据结构的实现
1.顺序表
顺序表是线性表的一种,满足逻辑结构和物理结构双线性
逻辑结构:数组元素之间呈"一对一"的先后顺序,是逻辑上的线性结构,可能与实际结构并不相同
物理结构:底层基于数组实现,数组的内存空间是连续且不可分割,因此数据在物理存储上也连续
1.1.顺序表的结构:
点击查看代码
typedef struct SeqList {
SLdatatype* data;//数组的指针
int size;//有效数据的个数
int capacity;//数组的实际空间
}SL;
1.2.顺序表的接口:
点击查看代码
//初始化顺序表
void InitSL(SL* ps);
//销毁顺序表
void DestroySL(SL* ps);
//申请空间
void SLbuy(SL* ps, SLdatatype x);
//打印
void SLprint(SL ps);
//头插
void SLpushfront(SL* ps, SLdatatype x);
//尾插
void SLpushback(SL* ps, SLdatatype x);
//在指定位置之前插入数据
void SLInsert(SL* ps, int pos, SLdatatype x);
//尾删
void SLpopback(SL* ps);
//头删
void SLpopfront(SL* ps);
//删除指定位置的数据
void SLErase(SL* ps, int pos);
//查找
int SLFind(SL* ps, SLdatatype x);
1.3.顺序表的实现:
点击查看代码
//初始化
void InitSL(SL* ps) {
ps->data = NULL;
ps->capacity = ps->size = 0;
}
//销毁
void DestroySL(SL* ps) {
if (ps->data) {
free(ps->data);
}
ps->data = NULL;
ps->capacity = ps->size = 0;
}
//打印顺表表中的元素
void SLprint(SL s) {
for (int i = 0; i < s.size; i++) {
printf("%d", s.data[i]);
}
printf("\n");
}
//申请空间
void SLbuy(SL* ps) {
//如果不这样capacity = 0 时,capacity就永远为0
int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
//这里是relloc(扩容),如果是malloc就是重新开辟了一块空间,那么原来的数据就丢失了
SLdatatype* tmp = (SLdatatype*)realloc(ps->data, newcapacity * sizeof(SLdatatype));
if (tmp == NULL) {
perror("SLpushback():realloc Fail");
exit(1);
}
//这里申请完空间后注意重新赋值capacity
ps->capacity = newcapacity;
ps->data = tmp;
}
//尾插
void SLpushback(SL* ps,SLdatatype x) {
assert(ps);
if (ps->capacity == ps->size) {
SLbuy(ps);
}
//push完size++
ps->data[ps->size++] = x;
}
//头插
void SLpushfront(SL* ps, SLdatatype x) {
assert(ps);
if (ps->capacity == ps->size) {
SLbuy(ps);
}
for (int i = ps->size; i > 0; i--) {
ps->data[i] = ps->data[i - 1];
}
//push完size++
ps->data[0] = x;
ps->size++;
}
//任意位置插入
void SLInsert(SL* ps, int pos, SLdatatype x) {
assert(ps);
//防止越界的问题
assert(pos >= 0 && pos <= ps->size);
if (ps->capacity == ps->size) {
SLbuy(ps);
}
for (int i = ps->size; i > pos; i--) {
ps->data[i] = ps->data[i - 1];
}
ps->data[pos] = x;
ps->size++;
}
//尾删
void SLpopback(SL* ps) {
assert(ps);
assert(ps->size);
//删完后size--
--(ps->size);
}
//头删
void SLpopfront(SL* ps) {
assert(ps);
assert(ps->size);
for (int i = 0; i < ps->size - 1; i++) {
ps->data[i] = ps->data[i + 1];
}
--(ps->size);
}
//任意位置删
void SLErase(SL* ps, int pos) {
assert(ps);
assert(pos >= 0 && pos < ps->size);
for (int i = pos; i<ps->size-1; i++) {
ps->data[i] = ps->data[i + 1];
}
ps->size--;
}
int SLFind(SL* ps, SLdatatype x) {
assert(ps);
for (int i = 0; i < ps->size; i++) {
if (ps->data[i] == x) {
return i;
break;
}
}
//只要返回无效的下标就行
return -1;
}
2.链表
逻辑结构线性,物理结构离散
逻辑结构:数据元素之间通过指针建立"一对一"的先后顺序,逻辑上呈线性。
物理结构:节点的内存地址并不连续,不能连续访问
2.1.链表的结构:
点击查看代码
typedef int SlDatatype;
typedef struct Slistnode {
SlDatatype data;
struct Slistnode* next;
}Slnode;
2.2.链表的接口:
点击查看代码
//链表的申请空间
Slnode* SlistBuy(SlDatatype x);
//链表的打印
void SlistPrint(Slnode* phead);
//链表的尾插
void SlistPushback(Slnode** phead, SlDatatype data);
//链表的头插
void SlistPushhead(Slnode** pphead, SlDatatype data);
//链表的尾删
void Slistdeleteback(Slnode** pphead);
//链表的头删
void Slistdeletehead(Slnode** pphead);
//链表的查找
Slnode* SlistFind(Slnode** pphead, SlDatatype x);
//链表指定位置之前插入节点
void Slistinert(Slnode** pphead, Slnode* pos, SlDatatype x);
//链表指定位置之后插入节点
void Slistinertback(Slnode* pos, SlDatatype x);
//链表指定位置删除节点
void SlistErase(Slnode** pphead, Slnode* pos);
//链表指定位置之后删除节点
void SlistsEraseBack(Slnode* pos);
2.3.链表的实现:
点击查看代码
//申请空间
Slnode* SlistBuy(SlDatatype x) {
Slnode* newnode = (Slnode*)malloc(sizeof(Slnode));
if (newnode == NULL) {
perror("malloc fail");
exit(1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
//链表的打印
void SlistPrint(Slnode* phead) {
Slnode* tmp = phead;
while (tmp) {
printf("%d->", tmp->data);
tmp=tmp->next;
}
printf("NULL\n");
}
//链表的尾插->传二级指针,因为只要涉及改变参数的都要地址拷贝
void SlistPushback(Slnode** pphead, SlDatatype data) {
//寻找尾部
assert(pphead);
Slnode* tmp = *pphead;
Slnode*newnode = SlistBuy(data);
if (tmp== NULL) {
*pphead = newnode;
}
else {
while (tmp->next) {
tmp=tmp->next;
}
tmp->next = newnode;
newnode->data = data;
newnode->next = NULL;
}
}
//链表的头插
void SlistPushhead(Slnode** pphead, SlDatatype data) {
assert(pphead);
Slnode* tmp = *pphead;
Slnode* newnode = SlistBuy(data);
if (tmp == NULL) {
*pphead= newnode;
}
else {
*pphead = newnode;
newnode->data = data;
newnode->next = tmp;
}
}
//链表的尾删
void Slistdeleteback(Slnode** pphead) {
assert(pphead && *pphead);
Slnode* tmp = *pphead;
Slnode* prev = *pphead;
if (tmp -> next ==NULL) {
free(*pphead);
*pphead = NULL;
}
else {
while (tmp->next) {
prev = tmp;
tmp = tmp->next;
}
}
free(tmp);
tmp = NULL;
prev->next = NULL;
}
void Slistdeletehead(Slnode** pphead) {
assert(pphead && *pphead);
Slnode* cmp = *pphead;
*pphead = cmp->next;
free(cmp);
cmp = NULL;
}
void Slistinert(Slnode** pphead, Slnode* pos, SlDatatype x) {
assert(pphead&&pos&&*pphead);
Slnode* newnode = SlistBuy(x);
Slnode* prev = *pphead;
Slnode* pur = *pphead;
if (pos == *pphead) {
SlistPushhead(pphead, x);
}
else {
while (pur != pos) {
prev = pur;
pur = pur->next;
}
prev->next = newnode;
newnode->next = pur;
}
}
Slnode* SlistFind(Slnode** pphead, SlDatatype x) {
assert(pphead && *pphead);
int Flag = 0;
Slnode* tmp = *pphead;
while (tmp) {
if (tmp->data == x) {
Flag = 1;
return tmp;
}
tmp = tmp->next;
}
if (Flag == 0) {
return NULL;
}
}
void Slistinertback(Slnode* pos, SlDatatype x) {
assert(pos);
Slnode* newnode = SlistBuy(x);
newnode->next = pos->next;
pos->next = newnode;
}
void SlistErase(Slnode** pphead, Slnode* pos) {
assert(pphead && pos);
Slnode* prev = *pphead;
Slnode* pur = *pphead;
if (pos == *pphead) {
Slnode* toDel = *pphead;
*pphead = toDel->next;
free(toDel);
return;
}
while (pur != pos) {
prev = pur;
pur = pur->next;
}
prev->next = pur->next;
free(pur);
pur = NULL;
}
void SlistsEraseBack(Slnode* pos) {
assert(pos&&pos->next);
Slnode* tmp = pos->next;
pos->next = tmp->next;
free(tmp);
tmp = NULL;
}
简单总结一下链表和顺序表的不同点:
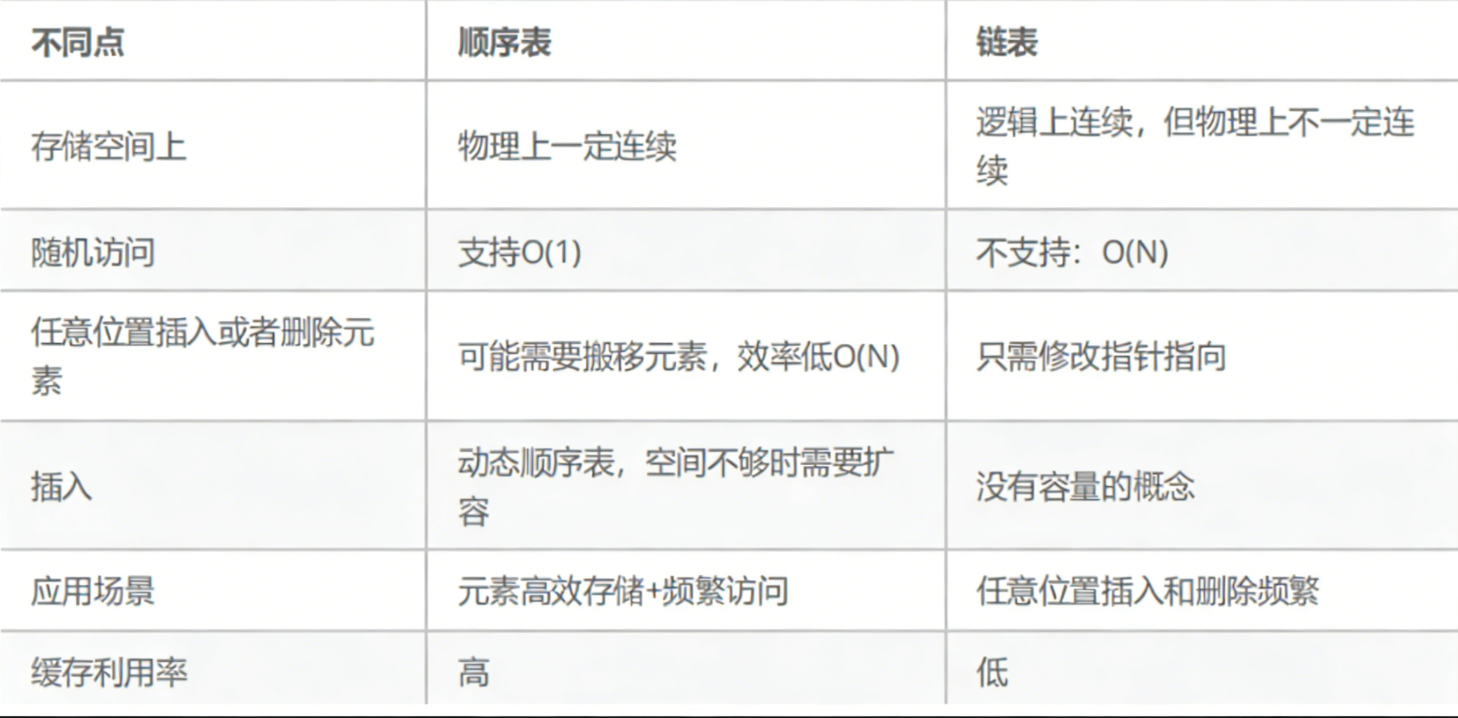
缓存:由于CPU的运行速率超快,与内存不同频,需要把内存中的内容先转到寄存器中,而寄存器由于空间有限,所以要先转到缓存器中,然后等寄存器运行结束后,再将缓存器中的内容转到寄存器中。(简单的理解)
顺序表的缓存利用率高:数组由于空间连续,缓存器一次取顺序表的内容就可以一大片一大片的取,缓存命中率就高,而链表由于空间不一定连续,所以就只能一次一次的取,效率就慢,缓存命中率就低。
3.栈
栈是一种后进先出的线性表,仅允许在栈顶进行插入和删除
3.1.栈的实现选择:如果是用链表实现,我们就需要频繁的找尾,而每次找尾的时间复杂度为O(N),并且再删除尾部的时候还要保存上一节点,操作繁琐。所以我们选择了更易操作的数组实现。
3.2.栈的结构:
点击查看代码
typedef int STdatatype;
typedef struct Stack {
STdatatype* a;
int top;
int capacity;
}ST;
3.3.栈的接口:
点击查看代码
//栈的初始化
void STinit(ST* pst);
//栈的销毁
void STdestroy(ST* pst);
//入栈
void STpush(ST* pst,STdatatype x);
//出栈
void STpop(ST* pst);
//取栈顶数据
STdatatype STtop(ST* pst);
//判空
int STempty(ST* pst);
//获取数据个数
int STsize(ST* pst);
3.4.栈的实现:
点击查看代码
void STinit(ST* pst) {
pst->a = NULL;
pst->capacity = pst->top = 0;
}
void STdestroy(ST* pst) {
assert(pst);
free(pst->a);
pst->a = NULL;
pst->capacity = pst->top = 0;
}
void STpush(ST* pst,STdatatype x) {
assert(pst);
if (pst->capacity == pst->top) {
int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
STdatatype* tmp = (STdatatype*)realloc(pst->a,newcapacity*sizeof(STdatatype));
if (tmp == NULL) {
perror("STPush():realloc():Fail");
return;
}
pst->capacity = newcapacity;
pst->a = tmp;
}
pst->a[pst->top++] = x;
}
void STpop(ST* pst) {
assert(pst);
assert(pst->top);
pst->top--;
}
STdatatype STtop(ST* pst) {
assert(pst);
assert(pst->top);
return pst->a[pst->top - 1];
}
int STempty(ST* pst) {
assert(pst);
return pst->top == 0;
}
int STsize(ST* pst) {
assert(pst);
int size = pst->top;
return size;
}
利用栈可以解决经典算法题(https://leetcode.cn/problems/valid-parentheses/)
思路:
1.若遇到左括号就入栈
2.若遇到右括号就尝试与栈顶的左括号匹配
代码实现:
点击查看代码
bool isValid(char* s) {
ST st;
STinit(&st);
//遍历字符串
while(*s){
//如果是左括号就入栈
if(*s == '(' || *s == '[' || *s == '{'){
STpush(&st,*s);
}
//如果是右括号就尝试与左括号匹配
else{
if(STempty(&st)){
STdestroy(&st);
return false;
}
char top = STtop(&st);
STpop(&st);
if((top == '(' && *s != ')') ||
(top == '[' && *s != ']') ||
(top == '{' && *s != '}')){
STdestroy(&st);
return false;
}
}
++s;
}
bool ret = STempty(&st);
STdestroy(&st);
return ret;
}
4.队列
队列是一种先进先出的线性表,在队头删除,在队尾插入
4.1.队列的应用:医院抽号机,还有社交平台上的好友推荐
4.2.队列的实现选择:如果用数组实现,每次删除的是首元素,这样首元素后面的元素就得向前移动,时间复杂度为O(N),所以我们用链表更易实现
4.3.队列的结构:特殊点:额外用一个结构体封装了它的头节点,尾节点,以及大小,这样传参数的时候就能只传一个参数了
点击查看代码
typedef int Qdatatype;
typedef struct QueueNode {
struct QueueNode* next;
Qdatatype val;
}QNode;
typedef struct Queue {
QNode* phead;
QNode* ptail;
int size;
}Queue;
4.4.队列的接口:
点击查看代码
//队列的初始化
void QueueInit(Queue* pq);
//队列的销毁
void QueueDestroy(Queue* pq);
//队头数据的删除
void QueuePop(Queue* pq);
//队尾插入数据
void QueuePush(Queue* pq, Qdatatype x);
//获取队头的数据
Qdatatype QueueFront(Queue* pq);
//获取队尾的数据
Qdatatype QueueBack(Queue* pq);
//队列的长度
int QueueSize(Queue* pq);
//队列的判空
bool QueueEmpty(Queue* pq);
4.5.队列的实现:
点击查看代码
void STinit(ST* pst) {
pst->a = NULL;
pst->capacity = pst->top = 0;
}
void STdestroy(ST* pst) {
assert(pst);
free(pst->a);
pst->a = NULL;
pst->capacity = pst->top = 0;
}
void STpush(ST* pst,STdatatype x) {
assert(pst);
if (pst->capacity == pst->top) {
int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
STdatatype* tmp = (STdatatype*)realloc(pst->a,newcapacity*sizeof(STdatatype));
if (tmp == NULL) {
perror("STPush():realloc():Fail");
return;
}
pst->capacity = newcapacity;
pst->a = tmp;
}
pst->a[pst->top++] = x;
}
void STpop(ST* pst) {
assert(pst);
assert(pst->top);
pst->top--;
}
STdatatype STtop(ST* pst) {
assert(pst);
assert(pst->top);
return pst->a[pst->top - 1];
}
int STempty(ST* pst) {
assert(pst);
return pst->top == 0;
}
int STsize(ST* pst) {
assert(pst);
int size = pst->top;
return size;
}
学了队列可以尝试一下这道题(https://leetcode.cn/problems/design-circular-queue/description/)
总结一下栈和队列的区别
栈和队列的核心区别就是:一个后进先出,一个先进先出
用两个队列实现栈(https://leetcode.cn/problems/implement-stack-using-queues/)
用两个栈实现队列(https://leetcode.cn/problems/implement-queue-using-stacks/)
思路如下:
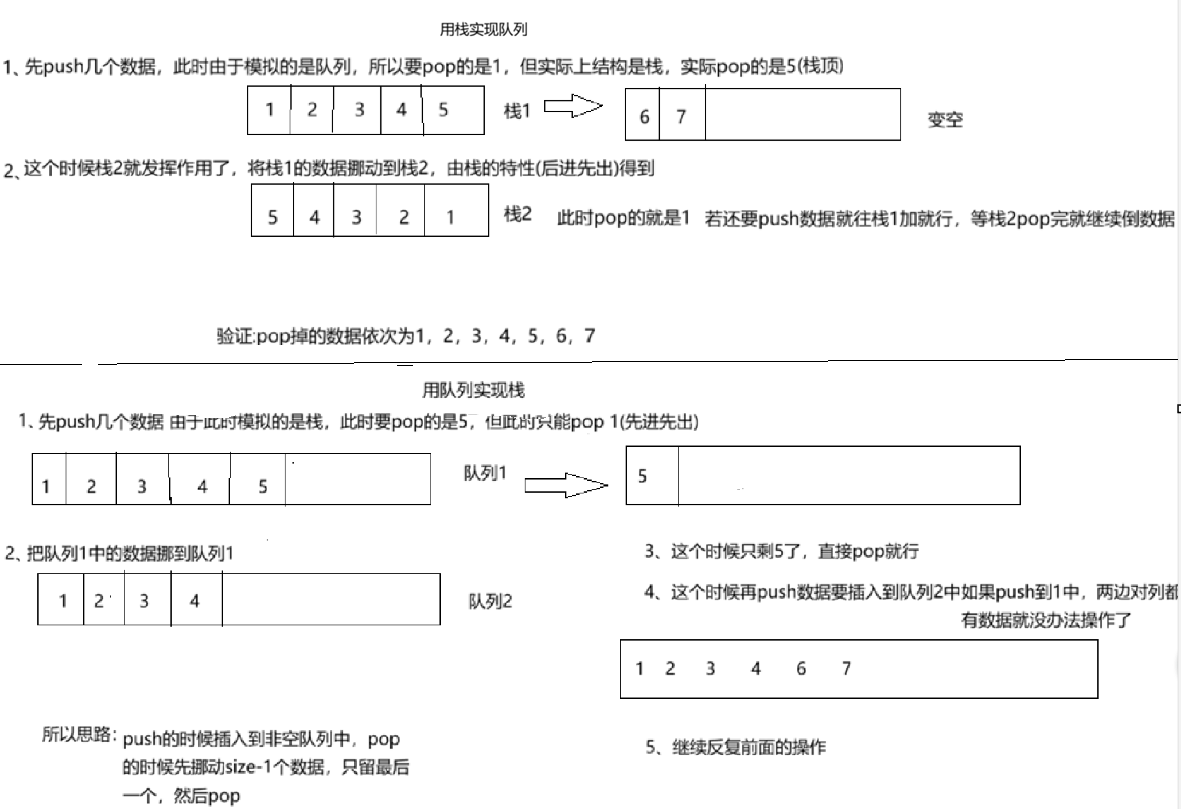
5.堆
特殊的完全二叉树,分为大堆和小堆
大堆:父节点>=子节点
小堆:父节点<=子节点
5.1.堆的存储特性:
物理上基于数组存储,逻辑上表现为完全二叉树
对于一个下标为i的节点:
若存在子节点
左孩子的节点下标:2i + 1
右孩子的节点下标:2i + 2
父节点下标:(i - 1)/2
5.2.堆的结构:
点击查看代码
typedef int Hpdatatype;
//堆(完全二叉树)的底层还是一个数组
typedef struct Heap {
Hpdatatype* a;
int size;
int capacity;
}Heap;
5.3.堆的接口:
点击查看代码
//交换函数
void Swap(Hpdatatype* ph1, Hpdatatype* ph2);
//向上调整法
void AdjustUp(Hpdatatype* a, int child);
//向下调整法
void AdjustDown(Hpdatatype* a, int size, int parent);
//堆的初始化
void HeapInit(Heap* php);
//堆的销毁
void HeapDestroy(Heap* php);
//堆的插入数据
void HeapPush(Heap* php, Hpdatatype x);
//堆的删除堆顶数据
void HeapPop(Heap*php);
//堆的获取堆顶数据
Hpdatatype HeapTop(Heap* php);
//堆的判空
bool HeapEmpty(Heap* php);
5.4.堆的实现:
点击查看代码
void HeapInit(Heap* php) {
assert(php);
php->a = NULL;
php->capacity = php->size = 0;
}
void HeapDestroy(Heap* php) {
assert(php);
php->a = NULL;
php->capacity = php->size = 0;
}
void Swap(Hpdatatype* hp1, Hpdatatype* hp2) {
assert(hp1 && hp2);
Hpdatatype tmp = *hp1;
*hp1 = *hp2;
*hp2 = tmp;
}
void HeapPush(Heap* php, Hpdatatype x) {
//实现小堆
int child = php->size;
int parent = (child - 1) / 2;
//判断空间够不够
if (php->capacity == php->size) {
int newcapacity = php->capacity == 0 ? 4 : 2 * (php->capacity);
Hpdatatype* tmp = (Hpdatatype*)realloc(php->a,newcapacity * sizeof(Hpdatatype));
if (tmp == NULL) {
perror("HeapPush():realloc():fail");
return;
}
php->capacity = newcapacity;//变化过后capacity没有改变
php->a = tmp;
}
php->a[child] = x;
php->size++;
//当child = 0 的时候停止
AdjustUp(php->a, child);
}
void HeapPop(Heap* php) {
//每次pop的意义是把次小的数推上堆顶
assert(php);
assert(php->size);
//首先先将堆顶的数据与堆尾的数据交换
Swap(&php->a[0], &php->a[php->size - 1]);
--php->size;
//再使用向下查找算法
AdjustDown(php->a, php->size, 0);
}
Hpdatatype HeapTop(Heap* php) {
assert(php);
assert(php->size);
return php->a[0];
}
bool HeapEmpty(Heap* php) {
assert(php);
return php->size == 0;
}
void AdjustUp(Hpdatatype* a, int child){
//向上和向下调整法的时间复杂度都为O(N)
int parent = (child - 1) / 2;
while (child > 0) {
//如果不满足就重复交换child 和 parent 的值
if (a[child] < a[parent]) {
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
//当child > parent 的时候停止
else {
break;
}
}
}
void AdjustDown(Hpdatatype * a, int size, int parent) {
int lesschild = 2 * parent + 1;
//结束条件是到达叶子
while (lesschild < size) {
//假设法找到字节点中较小的那个
if (lesschild + 1<size && a[lesschild] > a[lesschild + 1]) {
lesschild++;
}
//将较小的子节点与父节点相比较
if (a[lesschild] < a[parent]) {
Swap(&a[lesschild], &a[parent]);
parent = lesschild;
lesschild = 2 * parent + 1;
}
else {
break;
}
}
}
5.5.堆排序:
点击查看代码
void HeapSort(Hpdatatype* a, int size) {
int parent = (size - 2) / 2;
while (parent--) {
AdjustDown(a, size, parent);//已经调成小堆的形式
}
while (size) {
Swap(&a[0], &a[size - 1]);
size--;
AdjustDown(a, size, 0);
}
}
三、结语
数据结构是计算机学科的基石,掌握顺序表、链表、栈、队列、堆的核心特性和实现,是后续学习树、图、排序算法的基础。建议结合LeetCode算法题反复练习,将理论转化为实战能力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号