实验一 顺序表与链表
|这个作业属于哪个课程| https://edu.cnblogs.com/campus/qdu/DS2020| |
|这个作业要求在哪里 | https://edu.cnblogs.com/campus/qdu/DS2020| ---- |
|这个作业的目标| 理解线性表顺序表和链表,掌握顺序表与链表的建立插入删除元素的算法,分析复杂度并调试程序 |
一、实验目的
1、掌握线性表中元素的前驱、后续的概念。
2、掌握顺序表与链表的建立、插入元素、删除表中某元素的算法。
3、对线性表相应算法的时间复杂度进行分析。
4、理解顺序表、链表数据结构的特点(优缺点)。
二、实验预习
说明以下概念
1、线性表:线性表是零个或多个数据元素的有限序列
2、顺序表:将元素顺序地存放在一块连续的存储区里,元素间的顺序关系由它们的存储顺序自然表示。
3、链表:将元素存放在通过链接构造起来的一系列存储块中。
三、实验内容和要求
1、阅读下面程序,在横线处填写函数的基本功能。并运行程序,写出结果。
#include<stdio.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
#define INIT_SIZE 5 /*初始分配的顺序表长度*/
#define INCREM 5 /*溢出时,顺序表长度的增量*/
typedef int ElemType; /*定义表元素的类型*/
typedef struct Sqlist{
ElemType *slist; /*存储空间的基地址*/
int length; /*顺序表的当前长度*/
int listsize; /*当前分配的存储空间*/
}Sqlist;
int InitList_sq(Sqlist *L); /* 初始化顺序表L,并将其长度设为0 */
int CreateList_sq(Sqlist *L,int n); /* 构造顺序表的长度为n */
int ListInsert_sq(Sqlist *L,int i,ElemType e);/* 在顺序线性表L中第i个元素之前插入新元素e */
int PrintList_sq(Sqlist *L); /*输出顺序表的元素*/
int ListDelete_sq(Sqlist *L,int i); /*删除第i个元素*/
int ListLocate(Sqlist *L,ElemType e); /*查找值为e的元素*/
int InitList_sq(Sqlist *L){
L->slist=(ElemType*)malloc(INIT_SIZE*sizeof(ElemType));
if(!L->slist) return ERROR;
L->length=0;
L->listsize=INIT_SIZE;
return OK;
}/*InitList*/
int CreateList_sq(Sqlist *L,int n){
ElemType e;
int i;
for(i=0;i<n;i++){
printf("input data %d",i+1);
scanf("%d",&e);
if(!ListInsert_sq(L,i+1,e))
return ERROR;
}
return OK;
}/*CreateList*/
/*输出顺序表中的元素*/
int PrintList_sq(Sqlist *L){
int i;
for(i=1;i<=L->length;i++)
printf("%5d",L->slist[i-1]);
return OK;
}/*PrintList*/
int ListInsert_sq(Sqlist *L,int i,ElemType e){
int k;
if(i<1||i>L->length+1)
return ERROR;
if(L->length>=L->listsize){
L->slist=(ElemType*)realloc(L->slist,
(INIT_SIZE+INCREM)*sizeof(ElemType));
if(!L->slist)
return ERROR;
L->listsize+=INCREM;
}
for(k=L->length-1;k>=i-1;k--){
L->slist[k+1]= L->slist[k];
}
L->slist[i-1]=e;
L->length++;
return OK;
}/*ListInsert*/
/*在顺序表中删除第i个元素*/
int ListDelete_sq(Sqlist *L,int i){
}
/*在顺序表中查找指定值元素,返回其序号*/
int ListLocate(Sqlist *L,ElemType e){
}
int main(){
Sqlist sl;
int n,m,k;
printf("please input n:"); /*输入顺序表的元素个数*/
scanf("%d",&n);
if(n>0){
printf("\n1-Create Sqlist:\n");
InitList_sq(&sl);
CreateList_sq(&sl,n);
printf("\n2-Print Sqlist:\n");
PrintList_sq(&sl);
printf("\nplease input insert location and data:(location,data)\n");
scanf("%d,%d",&m,&k);
ListInsert_sq(&sl,m,k);
printf("\n3-Print Sqlist:\n");
PrintList_sq(&sl);
printf("\n");
}
else
printf("ERROR");
return 0;
}
运行结果

算法分析
首先要选择顺序表的动态存储方式进行顺序表结构的定义,然后在程序的开头进行顺序表各种操作函数和预定义的命令。接着写出各种操作函数的函数体。在main函数中,首先调用Initlist_sq(&s1)函数初始化,然后调用InitList_sq()创建顺序表,然后调用PrintList_sq()函数输出该顺序表中元素的值,然后调用ListInsert_sq()函数,进行插入操作,并输出插入新元素后的状态。
2、为第1题补充删除和查找功能函数,并在主函数中补充代码验证算法的正确性。
删除算法代码:
int listdeletesq(sqlist *L,int i)
{
int p;
if (i<1))||(i>L->length)) return ERROR;
for (p=i-1;p<L->length-1;p++)
{
L->slist[p]=L->slist[p+1];
}
L->length--;
return OK;
}
运行结果
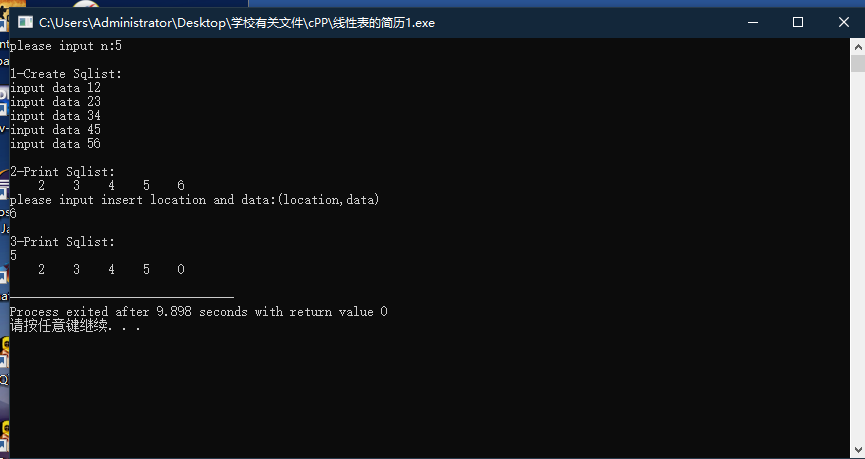
算法分析
在main函数中调用delete函数并传入参数后,程序将自动跳入函数体,用传递的参数逐级执行。在这个函数中,当序列表和序列号i被传入时,程序可以
首先判断传递的值是否满足条件。如果是,它将从序列表的第一个元素开始遍历,直到找到并删除位于i个位置的元素,然后向前移动并填充以下元素。表的长度减去1,删除成功。否则,返回0,表示删除失败。
查找算法代码:
int listlocate(sqlist *L,ElemType e)
{
int i=0;
while((i<=L->length)&&(L->slist[i]!=e))
i++;
if(i<=L->length)
return(i+1);
else
return(-1);
}
运行结果
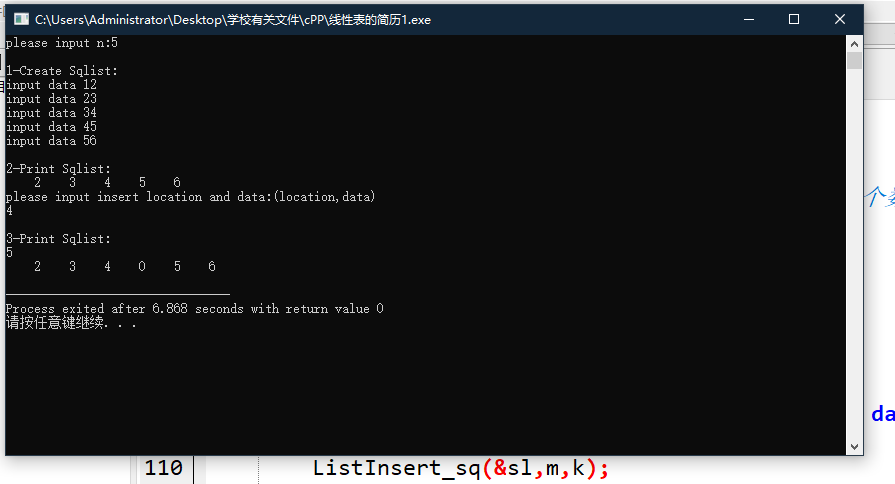
算法分析
当在主函数中调用搜索函数并传入参数时,程序将自动跳入函数体,使用传递的参数逐级执行。在这个函数中,当顺序表和要搜索的值e传入时,程序开始依次遍历顺序表的第一个元素,直到找到值为e的元素,并返回其位置序号,如果顺序表的所有元素都被遍历,并且没有满足条件,则返回0,表示搜索失败。
3、阅读下面程序,在横线处填写函数的基本功能。并运行程序,写出结果。
#include<stdio.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
typedef int ElemType; /*定义表元素的类型*/
typedef struct LNode{ /*线性表的单链表存储*/
ElemType data;
struct LNode *next;
}LNode,*LinkList;
LinkList CreateList(int n); /* 构造顺序表的长度 */
void PrintList(LinkList L); /*输出带头结点单链表的所有元素*/
int GetElem(LinkList L,int i,ElemType *e); /* 在顺序线性表L中,当第i个元素存在时,将其赋值为e */
LinkList CreateList(int n){
LNode *p,*q,*head;
int i;
head=(LinkList)malloc(sizeof(LNode)); head->next=NULL;
p=head;
for(i=0;i<n;i++){
q=(LinkList)malloc(sizeof(LNode)); printf("input data %i:",i+1);
scanf("%d",&q->data); /*输入元素值*/
q->next=NULL; /*结点指针域置空*/
p->next=q; /*新结点连在表末尾*/
p=q;
}
return head;
}/*CreateList*/
void PrintList(LinkList L){
LNode *p;
p=L->next; /*p指向单链表的第1个元素*/
while(p!=NULL){
printf("%5d",p->data);
p=p->next;
}
}/*PrintList*/
int GetElem(LinkList L,int i,ElemType *e){
LNode *p;int j=1;
p=L->next;
while(p&&j<i){
p=p->next;j++;
}
if(!p||j>i)
return ERROR;
*e=p->data;
return OK;
}/*GetElem*/
int main(){
int n,i;ElemType e;
LinkList L=NULL; /*定义指向单链表的指针*/
printf("please input n:"); /*输入单链表的元素个数*/
scanf("%d",&n);
if(n>0){
printf("\n1-Create LinkList:\n");
L=CreateList(n);
printf("\n2-Print LinkList:\n");
PrintList(L);
printf("\n3-GetElem from LinkList:\n");
printf("input i=");
scanf("%d",&i);
if(GetElem(L,i,&e))
printf("No%i is %d",i,e);
else
printf("not exists");
}else
printf("ERROR");
return 0;
}
运行结果
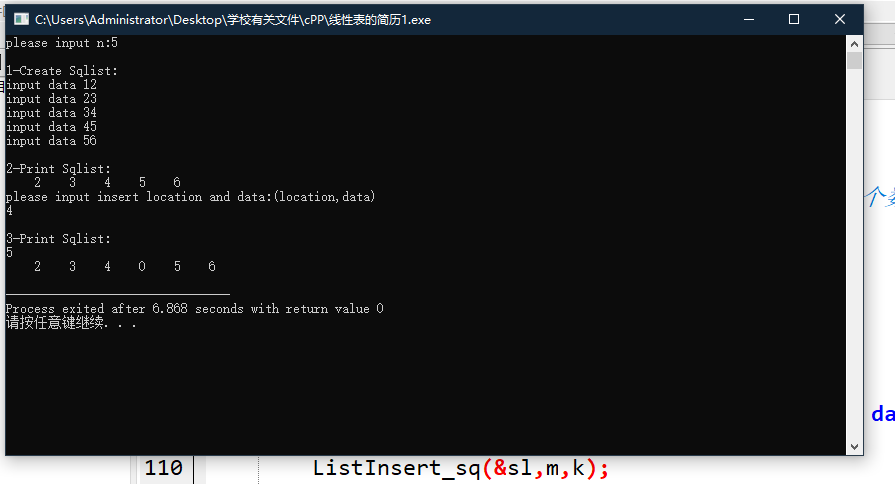
算法分析
首先定义单链表结构的定义,然后在程序的开头进行顺序表各种操作函数和预定义命令,然后编写各种操作函数的函数体。在main函数中,我们首先调用LinkList CreateList(int n)来创建带头结点的单链表,输入结点数,然后依次输入每个节点的值。然后调用打印单链表的函数,输出单链表中的值。然后调用查找函数,输入查找元素的位置,并输出相应元素的值。然后调用insert函数,输入要插入的位置和元素,插入后打印出新的链表。同样,调用删除功能函数,输入要删除的元素值,最后打印出删除后的单链列表。
4、为第3题补充插入功能函数和删除功能函数。并在主函数中补充代码验证算法的正确性。
插入算法代码:
int InsertList(LinkList L,int i,ElemType *e){
int j=1;LNode *p,*q;p=L->next;
while(p&&j<i-1)
{p=p->next;j++;}
if(!p) return ERROR;
q=(LNode*)malloc(sizeof(LNode));
q->data=*e;q->next=p->next;p->next=q;
return OK;
}
运行结果
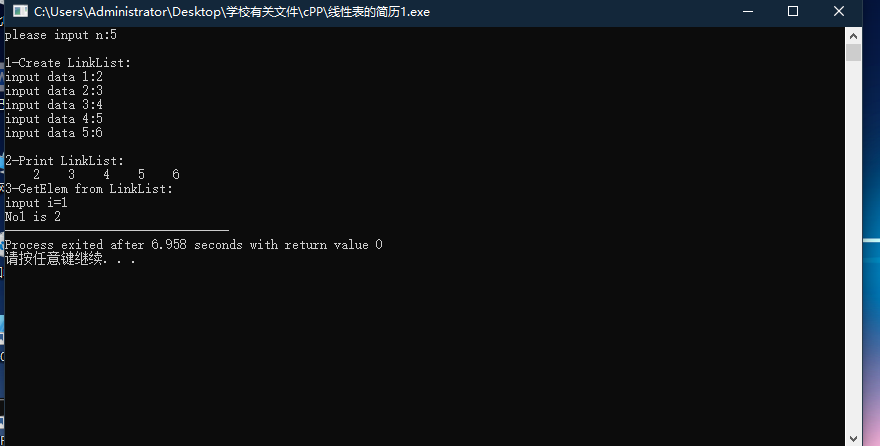
算法分析
单链表在找出某位置的指针后,插入时间复杂度:O(1)
步骤:
(1)创建带头结点的单链表,首先输入结点数,然后依次输入各个结点的值;
(2)输出单链表中的值;
(3)输入插入元素的位置和插入的元素,输出单链表中的值。
删除算法代码
void ListDelete(LinkList L, int i){
LNode *p, *q;
int j;
p=L; j=0;
while (p->next&&j<i-1) {
p=p->next;++j;
}
q=p->next;
p->next=q->next;
free (q) ;
}//ListDelete
运行结果
算法分析
顺序存储结构需要平均移动表长一半的元素,时间复杂度:O(n)
步骤:
(1)创建带头结点的单链表,首先输入结点数,然后依次输入各个结点的值;
(2)输出单链表中的值;
(3)输入删除元素的位置,输出单链表中的值。
以下为选做实验:
5. 循环链表的应用(约瑟夫回环问题)
n个数据元素构成一个环,从环中任意位置开始计数,计到m将该元素从表中取出,重复上述过程,直至表中只剩下一个元素。
提示:用一个无头结点的循环单链表来实现n个元素的存储。
算法代码
#include <stdio.h>
#include <stdlib.h>
#include<malloc.h>
typedef struct lnode{/*结点类型定义*/
int data;
struct lnode *next;
} node, *nodeptr;
nodeptr creat() {/*创建循环单链表*/
nodeptr l,p, q;
int i ,n, e;
printf(" please input numbers of nodes: " );
scanf("%d", &n);
l= (nodeptr)malloc(sizeof(node));
scanf(" %d",&e) ;
q=l;
q->data=e;
for(i=2;i<=n;i++) {
p= (nodeptr) malloc(sizeof (node));
scanf("%d" , &e) ;
p->data=e;
q->next=p;
q=p;
}
q->next=l;
return l;
}
int out (nodeptr l) {/*输出单链表的元素*/
nodeptr p;
p=l;
if(!p) return 0;
printf("%3d", p->data) ;
p=p->next;
while(p!=l) {
printf("%3d", p->data) ;
p=p->next;
}
printf("\n");
}
nodeptr joseph (nodeptr l){ /*约瑟夫回环函数*/
nodeptr p,q, r;
int val, k, m;
printf(" please input m:");
scanf("%d" , &m);
p=l;k=1;
while(p->next!=p)
if (k<m){
k++;
q=p;
p=p->next;
}
else{
val=p->data;
r=p;
p=p->next;
q->next=p;
printf("the value is %d\n", val);
free(r) ;
k=1;
}
l=p;
printf("last data is:%d\n",p->data) ;
return l;
}
int main(){/*主函数*/
nodeptr l;
l=creat();/*创建循环单链表*/
out(l);/*输出*/
joseph(l);/*求解约瑟夫回环问题*/
return 0;
}
运行结果
6.设一带头结点的单链表,设计算法将表中值相同的元素仅保留一个结点。
提示:指针p从链表的第一个元素开始,利用指针q从指针p位置开始向后搜索整个链表,删除与之值相同的元素;指针p继续指向下一个元素,开始下一轮的删除,直至p==null为至,既完成了对整个链表元素的删除相同值。
算法代码
#include <stdio.h>
#include <stdlib.h>
#include<malloc.h>
typedef struct lnode {/*结点类型定义*/
int data;
struct lnode *next;
} node, *nodeptr;
nodeptr creat() {/*创建带头结点的单链表*/
nodeptr l,p, q;
int i ,n, e;
l= (nodeptr) malloc (sizeof (node));
q=l;
q->next=0;
printf(" please input numbers of nodes: ");
scanf("%d" , &n) ;
for(i=1;i<=n;i++){
p= (nodeptr) malloc(sizeof (node));
scanf("%d", &e) ;
p->data=e;
q->next=p;
q=p;
q->next=0;
}
return l ;
}
void out (nodeptr l) { /*输出 单链表的元素*/
nodeptr p;
p=l->next;
while(p) {
printf("%3d", p->data) ;
p=p->next;
printf("\n");
}
}
nodeptr delete_list (nodeptr l) { /*删除算法,删除值相同的结点*/
nodeptr p,q,r,s;
int j,k;
p=l->next;
while(p){
q=p->next;r=p;
while(q)
if (p->data!=q->data){
r=q;
q=q->next;
}
else{
r->next=q->next;
s=q;q=r->next;
free(s);
}
p=p->next;
}
return l;
}
int main() {/*主函数*/
nodeptr l;
l=creat();/*创建单链表*/
out(l) ;/*输出*/
delete_list(l);/*调用删除算法,删除重复值*/
out(l) ;/*输出*/
return 0;
}
运行结果
四、实验小结
1.通过本次实验,理解线性表中元素的前驱、后续的概念。掌握顺序表与链表的建立、插入元素、删除表中某元素的算法。
2.对线性表相应算法的时间复杂度进行了分析。
理解顺序表、链表数据结构的特点(优缺点)。在空间性能中,
顺序存储结构需要预分配存储空间,分大了浪费,分小了易发生上溢。单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号