数据结构和算法

数据结构的存储方式只有两种：数组（顺序存储）和链表（链式存储）。

我们分析问题，一定要有递归的思想，自顶向下，从抽象到具体。你上来就列出这么多，那些都属于「上层建筑」，而数组和链表才是「结构基础」。因为那些多样化的数据结构，究其源头，都是在链表或者数组上的特殊操作，API 不同而已。

 

 DAG：Directed Acyclic Graph   有向无环图

 

 

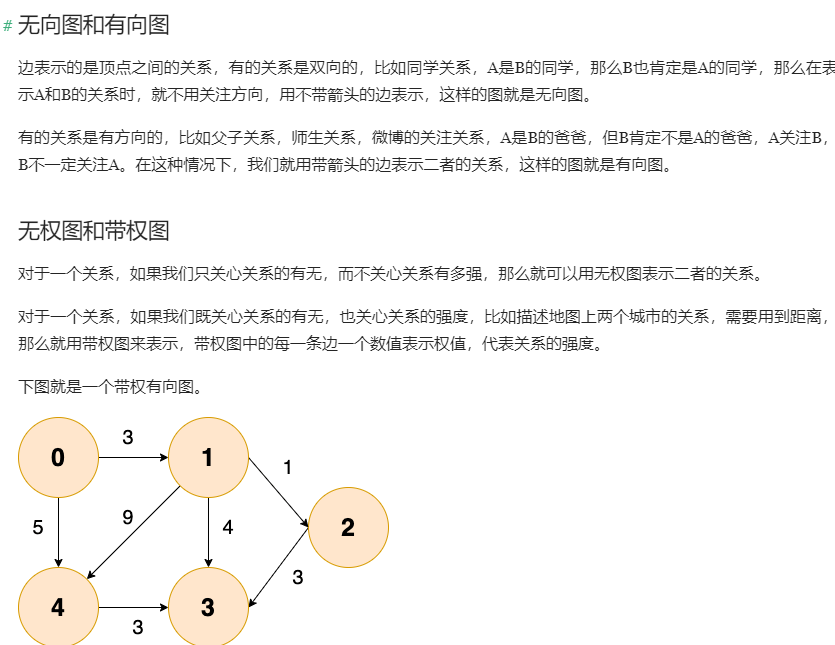
 图的搜索：

广度优先搜索和深度优先搜索，广度优先遍历使用了队列。深度优先遍历使用栈。

图（有向图和无向图）两种表示方法：邻接表和邻接矩阵。邻接矩阵一般用来表示稠密矩阵，邻接表用来表示稀疏矩阵。

临界矩阵：

 

 

 

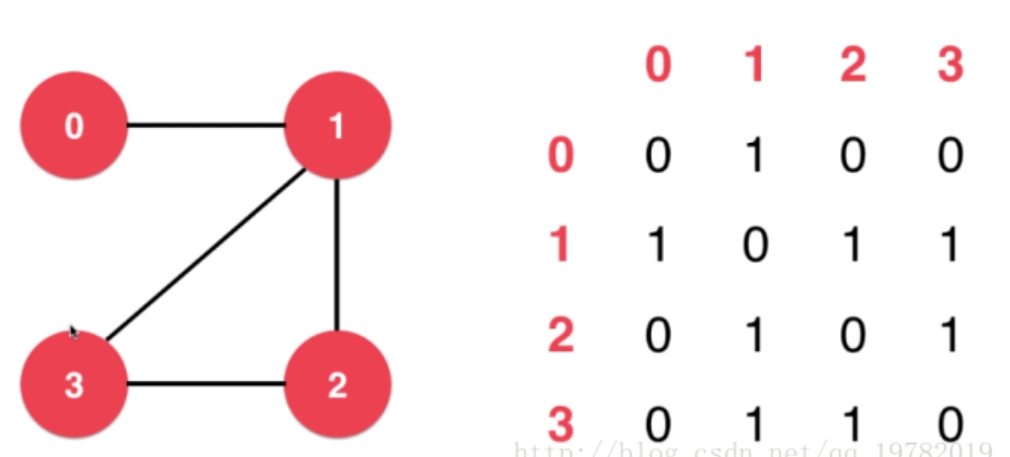
邻接表（一般用链表表示）：

 

 

 

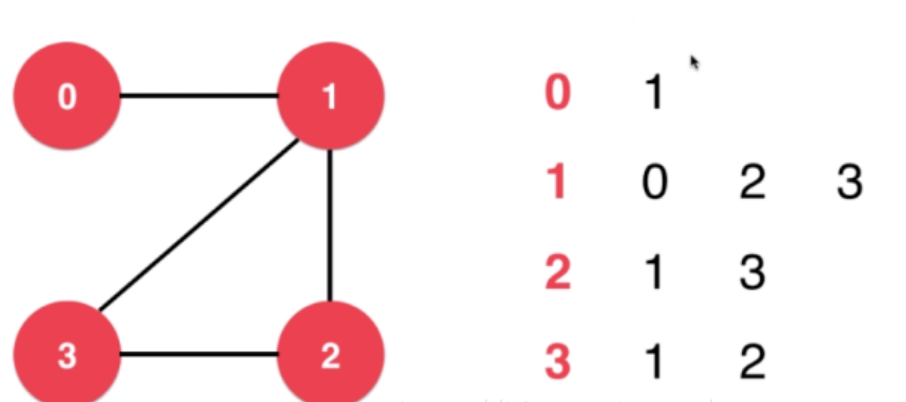
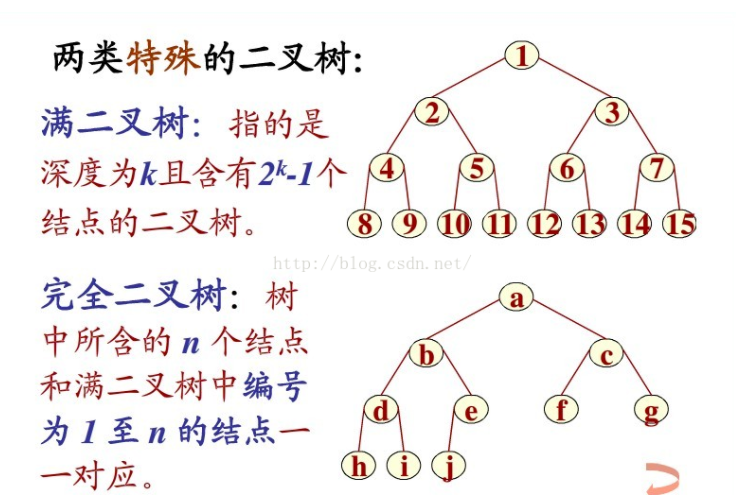
 树

树就是一种类似现实生活中的树的数据结构（倒置的树）。任何一颗非空树只有一个根节点。

一棵树具有以下特点：

1. 一棵树中的任意两个结点有且仅有唯一的一条路径连通。
2. 一棵树如果有 n 个结点，那么它一定恰好有 n-1 条边。
3. 一棵树不包含回路。

 

 

BST(Binary Search Tree)，二叉查找树

 特性：中序遍历是有序的。

1.左子树上所有结点的值均小于或等于它的根结点的值。

2.右子树上所有结点的值均大于或等于它的根结点的值。

3.左、右子树也分别为二叉排序树。

二叉查找树有缺陷，比如依次插入顺序的数值：9，8，7，6，5组成二叉查找树，就会变成每个节点只有左子树的树，也就是说退化成了链表。查找时间复杂度会退化成线性。

 

AVL树-自平衡的二叉查找树

AVL树本质上还是一棵二叉搜索树，它的特点是： 

1.本身首先是一棵二叉搜索树。

2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。

AVL树由于实现比较复杂，而且插入和删除性能差，在实际环境下的应用不如红黑树。

 

 红黑树

首先红黑树的优点：红黑树能够以O(log2(N))的时间复杂度进行搜索、插入、删除操作。此外,任何不平衡都会在3次旋转之内解决。这一点是AVL所不具备的。

1.节点是红色或黑色。

2.根节点是黑色。

3.每个叶子节点都是黑色的空节点（NIL节点）。

4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

 

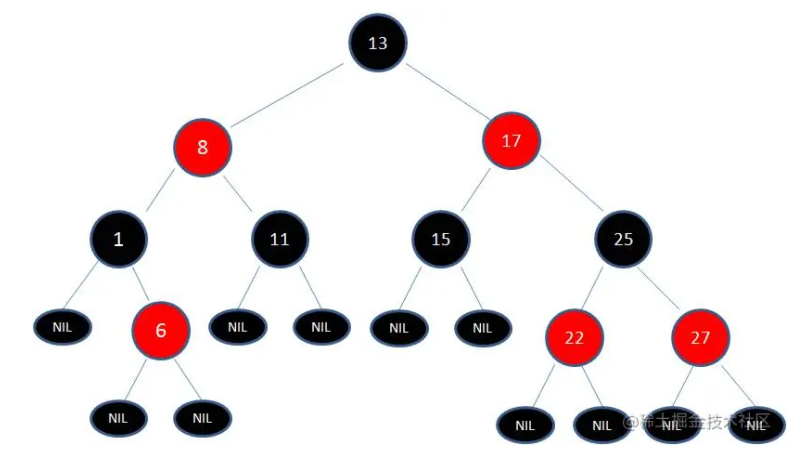
 为了保证性质5，从任意节点到根节点都经过相同数目的黑色节点，因此一般插入新节点都置为红色，如果不满足性质4，则需要进行变色，可能变色后会不满足性质5因此还需要进行旋转。

红黑树保证上面约束的调整手段：变色，左旋，右旋。

红黑树插入：

1、RBTree的插入与BST的插入方式是一致的，只不过是在插入过后，可能会导致树的不平衡，这时就需要对树进行旋转操作和颜色修复（在这里简称插入修复），使得它符合RBTree的定义。

2、新插入的节点是红色的，插入修复操作如果遇到父节点的颜色为黑则修复操作结束。也就是说，只有在父节点为红色节点的时候是需要插入修复操作的。

红黑树的删除：

1、删除操作首先需要做的也是BST的删除操作，删除操作会删除对应的节点，如果是叶子节点就直接删除，如果是非叶子节点，会用对应的中序遍历的后继节点来顶替要删除节点的位置。删除后就需要做删除修复操作，使的树符合红黑树的定义，符合定义的红黑树高度是平衡的。

2、删除修复操作在遇到被删除的节点是红色节点或者到达root节点时，修复操作完毕。

3、删除修复操作是针对删除黑色节点才有的，当黑色节点被删除后会让整个树不符合RBTree的定义的第四条。需要做的处理是从兄弟节点上借调黑色的节点过来，如果兄弟节点没有黑节点可以借调的话，就只能往上追溯，将每一级的黑节点数减去一个，使得整棵树符合红黑树的定义。

删除操作的总体思想是从兄弟节点借调黑色节点使树保持局部的平衡，如果局部的平衡达到了，就看整体的树是否是平衡的，如果不平衡就接着向上追溯调整。

 

堆

 堆是完全二叉树。一般用数组来表示堆。（纠正）

 

堆重要操作：

 

 

 

 

 

堆找父子节点计算公式：

 

 

 

 

 

 

 

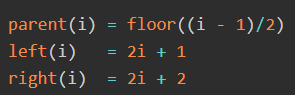
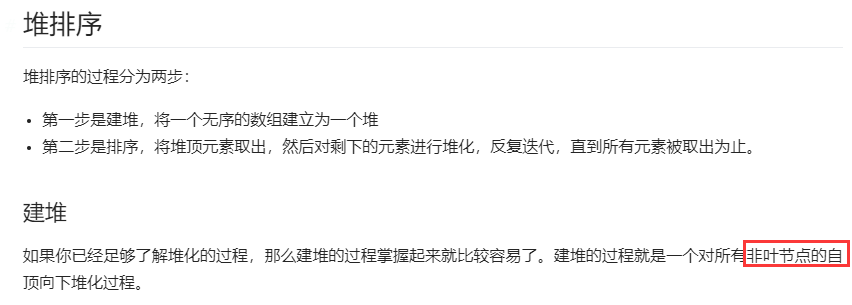
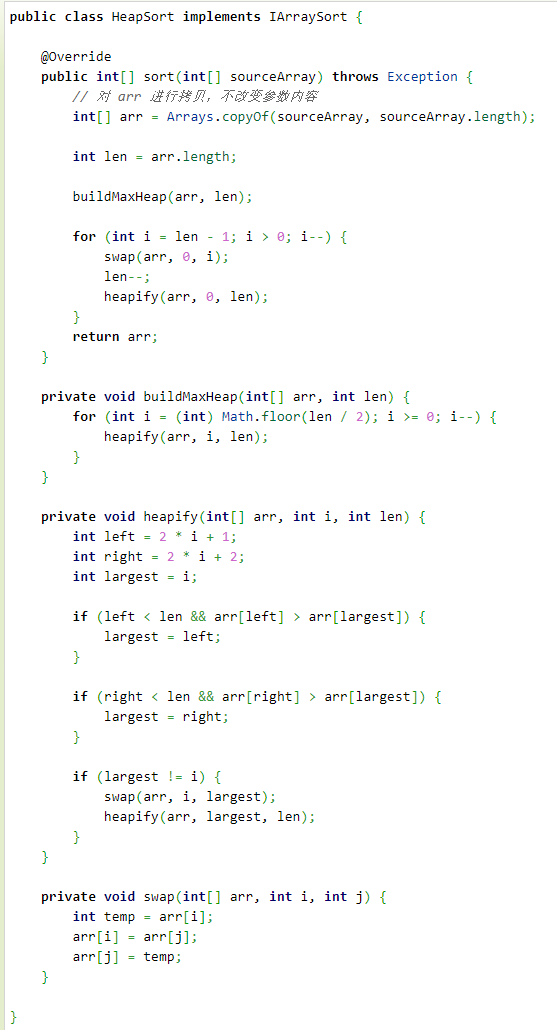
 堆排序代码：

 

哈夫曼树（最优树）