标准正态分布表_正态分布的简单计算

文章转自：https://blog.csdn.net/weixin_39521835/article/details/111235566

 

这里主要是指分位数、累积概率值与概率密度值的相互计算。三者之间的关系主要是曲线函数和概率函数。比如，知道分位数，要计算累积概率，或者计算概率密度值。 如下图所示，斜线面积部分为累积概率，累积范围为-∞到1，而该累积概率所对应的横轴位置1(A点)则称为其分位数；而图中B点为曲线中的一点，对应横坐标为1，而纵坐标值又是多少呢？这里B点即是正态分布的概率密度值。 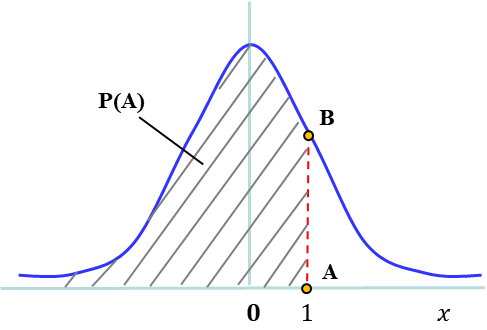 众所皆知，标准正态分布的平均值μ=0，标准差σ=1。在统计应用中，曲线之下与横轴的面积定义为1，那么，分位数为0时，累积概率就是0.5。对标准正态分布而言，概率值与分位数之间有标准表，只要知道分位数的大小，即可以查到概率值了。 对于非标准的正态分布，在手工计算时，则需要进行标准化的转换。假如已知正态分布的均值和方差，要求分位数为X的概率函数，按以下转换公式将分位数X进行转换，将得到新的分位数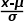，用新的分位数去查标准正态分布表即可。  简单去理解，曲线下方的面积为1，但不同的正态分布形状是不一样的，或胖或瘦，标准化转换的过程就是将胖的捏瘦，将瘦的拉胖，当形状变换成标准状态，其分位数也就改变了，仅此而已。 日常计算时，如果认为查表不方便的话，利用软件计算工具，是更好的方法。EXCEL或是WPS都可以进行简单计算。 EXCEL举例说明： 如下图所示，分位数和累积概率在分别在两单元格。累积概率单位格进行了函数设置。函数公式为=NORMDIST(A2,0,1,1)；  NORM.DIST函数四个填充项分别是分位数、均值、标准差、逻辑值。通过函数可以获得累积概率或者概率密度值。 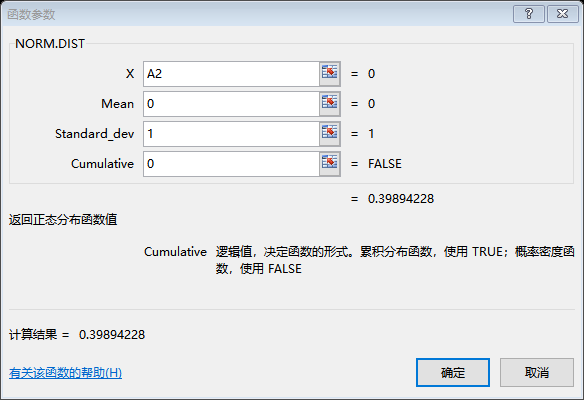 不同的填充项可以简单获得相应的结果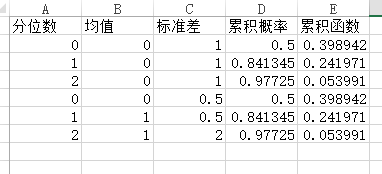：  用EXCEL输入不同的参数进行计算，从结果可以更深的理解三者的关系和正态分布的变化规律，可以多试试。 利用MINITAB也是可以进行同样的计算。 MINITAB举例说明： 打开计算>概率分布>正态，打开如下窗口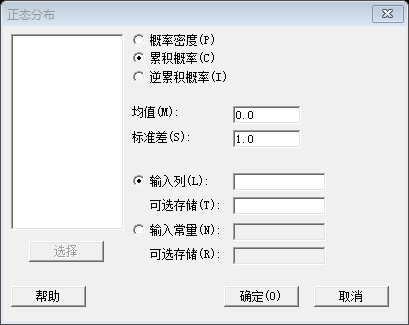：  先选择要计算结果的类型(逆累积概率即为分位数)，填写均值和标准差，然后输入数据即可，可以选择数据所在列，也可以直接输入。  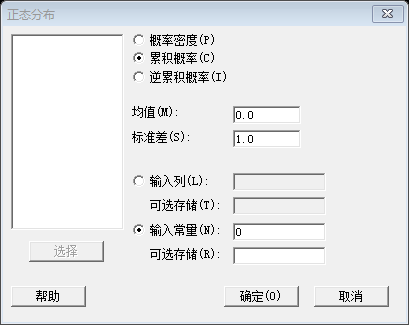如选择计算累积概率，在输入常量输入的即为分位数值，上图输入0(和均值相等)，即可得到累积概率为0.5的结果，如下截图：  到时，结束本次小课，你学会了吗？

https://blog.csdn.net/weixin_39521835/article/details/111235566