快速幂任意取模 UVA-374 Big Mod

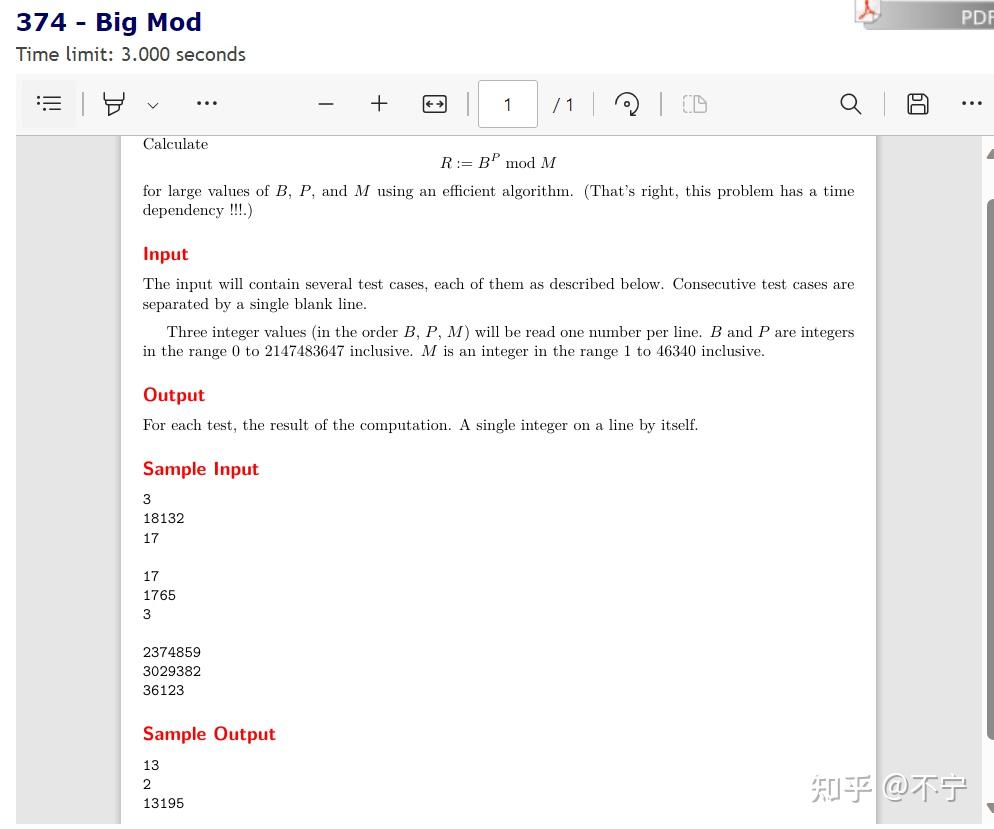
• **Calculate **

                                                             R= $B^{P}$  mod M

for large values of B,P, andM using an efficient algorithm. (That's right, this problem has a time dependency!!!.)

使用高效算法计算 B、P 和 M 的大数值。(没错，这个问题与时间有关！！！）。

• Input

The input will contain several test cases,each of them as described below.Consecutive test cases are separated by a single blank line. Three integer values(in the order B,P,M)will be read one number per line.B and P are integers in the range 0 to 2147483647 inclusive.M is an integer in the range 1 to 46340 inclusive.

连续的测试用例之间用空行隔开。 B 和 P 是范围在 0 到 2147483647（含）之间的整数，M 是范围在 1 到 46340（含）之间的整数。

• Output

For each test ,the result of the computation.A single integer on a line by itself.

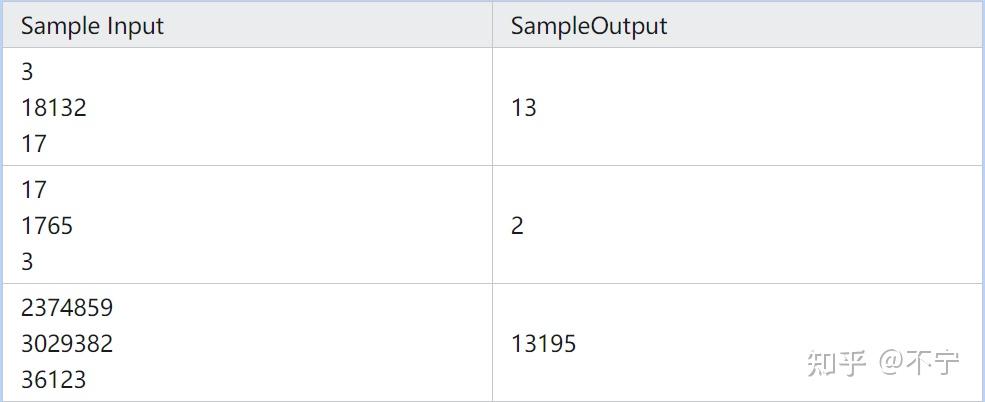
Sample Input	SampleOutput
3 18132 17	13
17 1765 3	2
2374859 3029382 36123	13195

AC代码

• 一个快速幂任意取模的题目。

对快速幂和大数取模有疑惑的同学可以看看之前的一篇（<~>）

不宁：快速幂和大数取模的简单运用(以SPOJ LASTDIG - The last digit为例）

#include <iostream>
typedef long long ll; 
#define endl '\n'
using namespace std;
 ll qpow(ll a,ll n,ll c)
{
    ll ans = 1;
    while(n)
    {
        if (n & 1) ans = ans * a % c;
        a = a * a % c;
        n >>= 1;//n >> 1可将原数减半,n >>= 1等价于n = n / 2
    }
    return ans;
}
int main()
{std::ios::sync_with_stdio(false);
     cin.tie(0);
     cout.tie(0);
     ll a,b;ll c;ll d;
  while(cin>>a>>b>>d){
	c=qpow(a,b,d);
	cout<<c<<endl;
}
    return 0;
}